



Практическое задание № 1
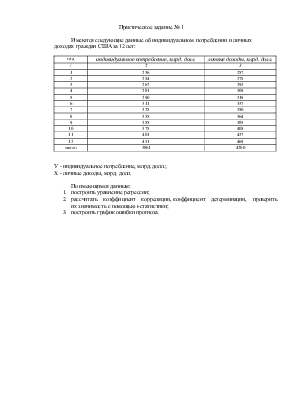
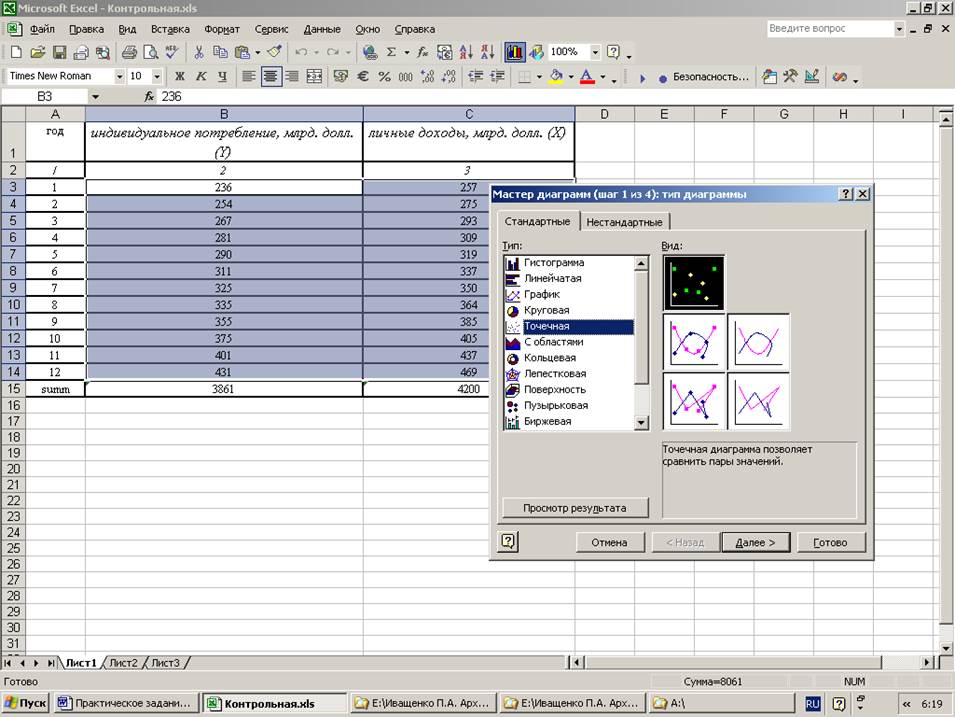
Имеются следующие данные об индивидуальном потреблении и личных доходах граждан США за 12 лет:
|
год |
индивидуальное потребление, млрд. долл. |
личные доходы, млрд. долл. |
|
/ |
2 |
3 |
|
1 |
236 |
257 |
|
2 |
254 |
275 |
|
3 |
267 |
293 |
|
4 |
281 |
309 |
|
5 |
290 |
319 |
|
6 |
311 |
337 |
|
7 |
325 |
350 |
|
8 |
335 |
364 |
|
9 |
355 |
385 |
|
10 |
375 |
405 |
|
11 |
401 |
437 |
|
12 |
431 |
469 |
|
summ |
3861 |
4200 |
У - индивидуальное потребление, млрд. долл.;
X - личные доходы, млрд. долл.
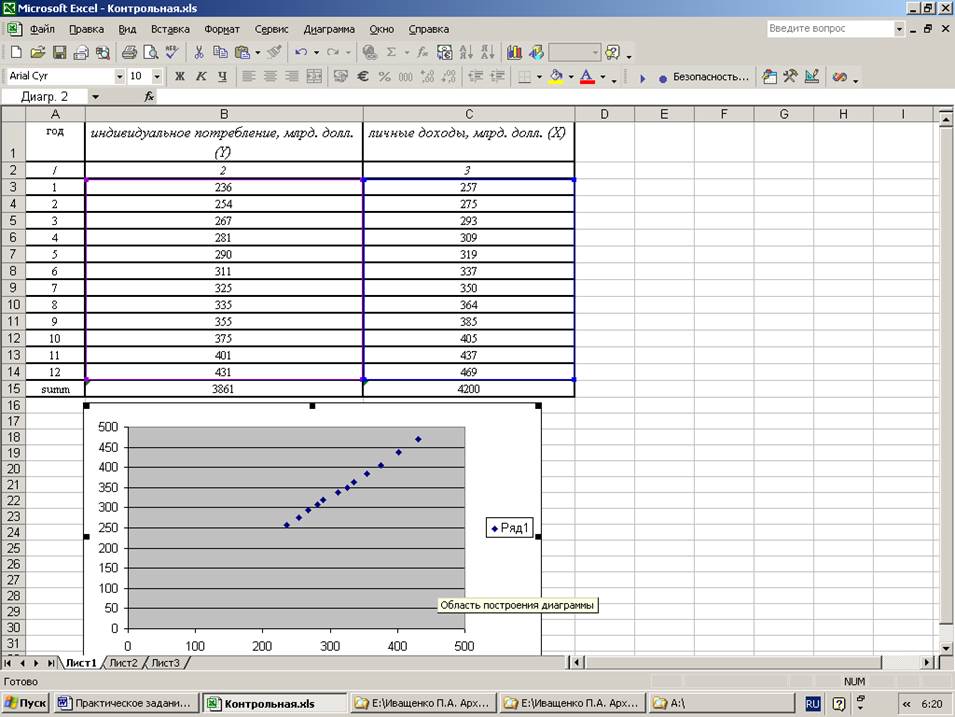
По имеющимся данным:
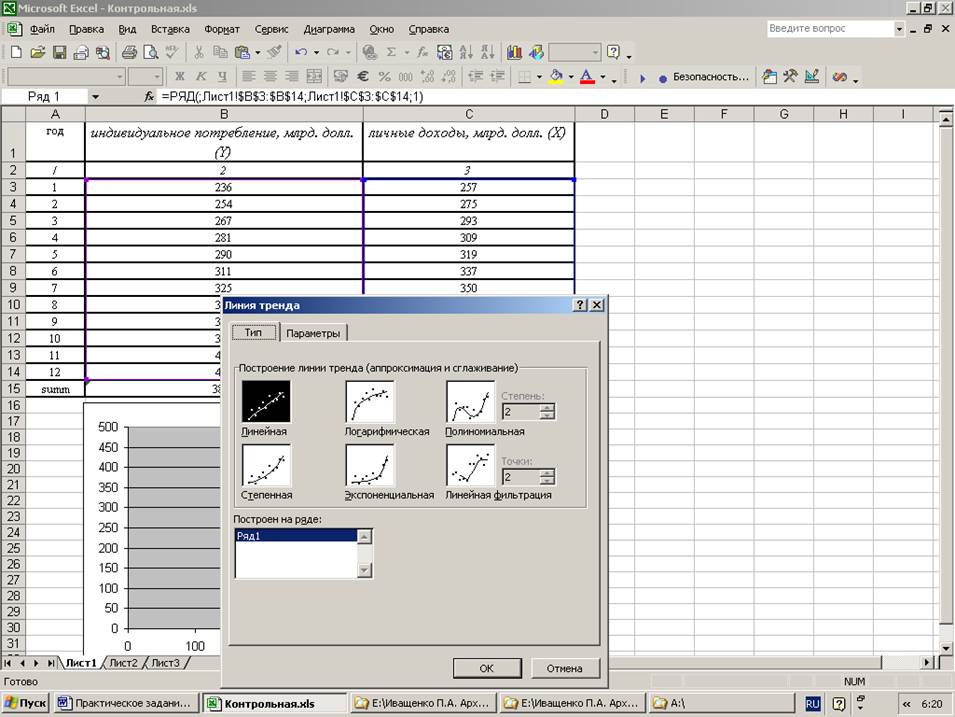
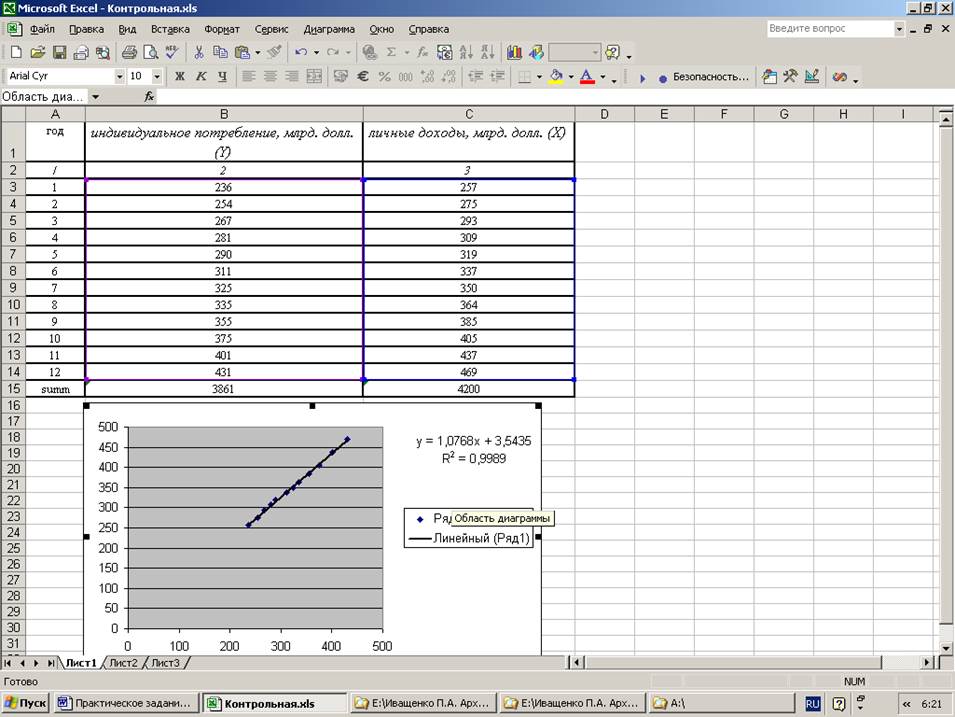
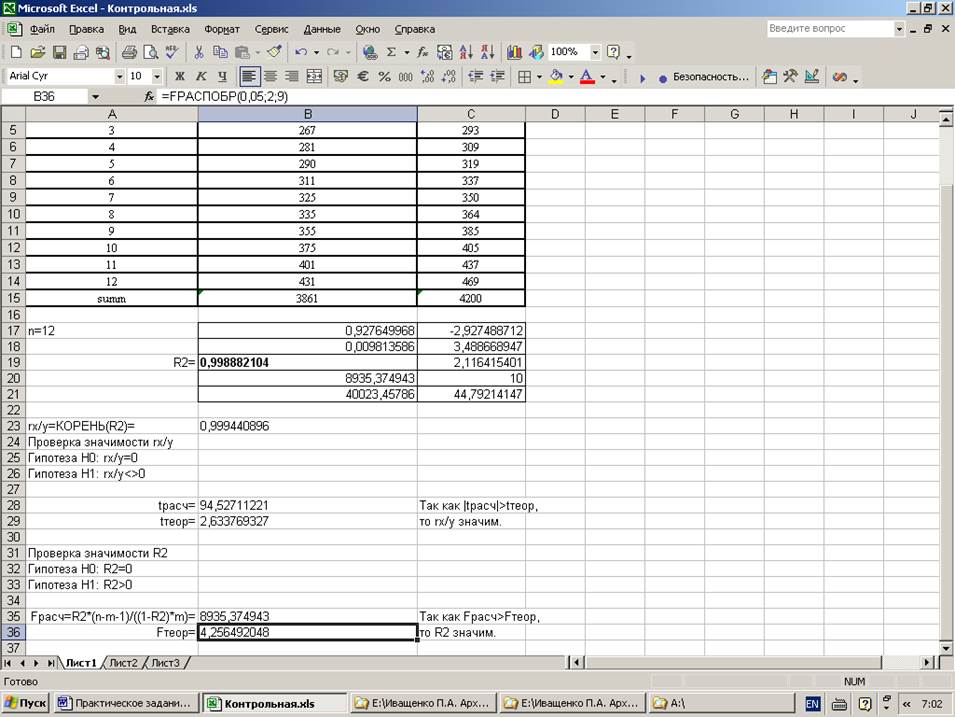
1. построить уравнение регрессии;
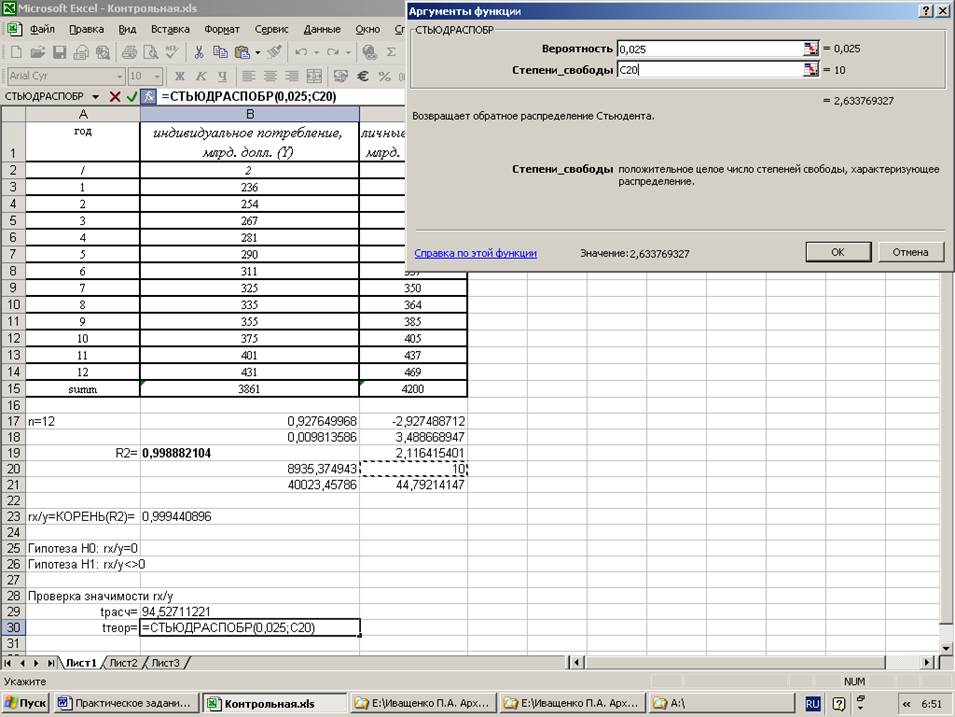
2. рассчитать коэффициент корреляции, коэффициент детерминации, проверить их значимость с помощью t-статистики;
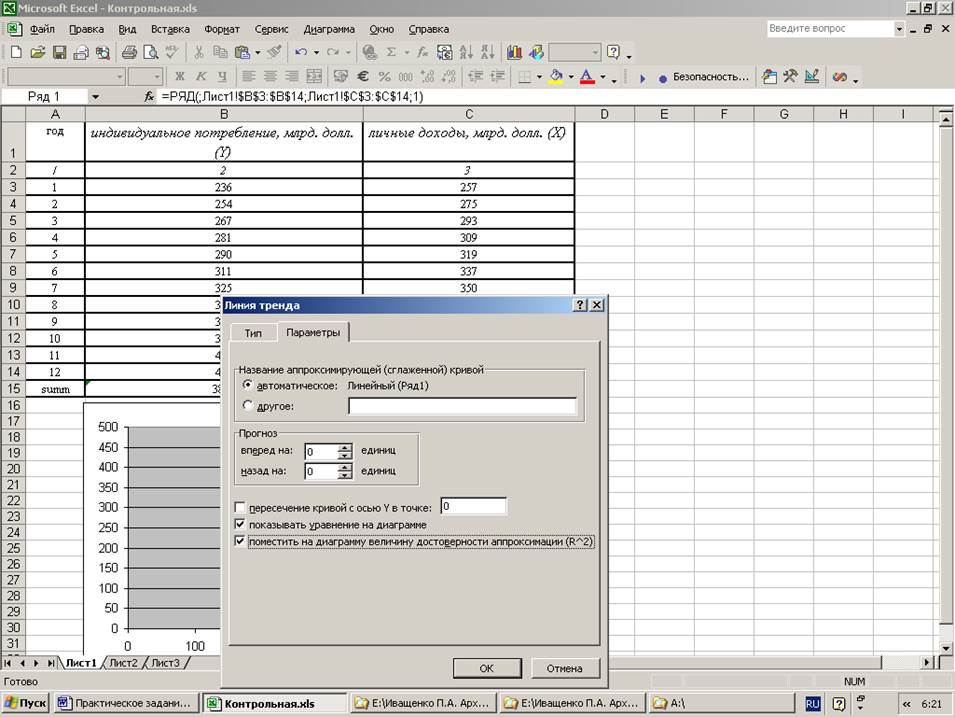
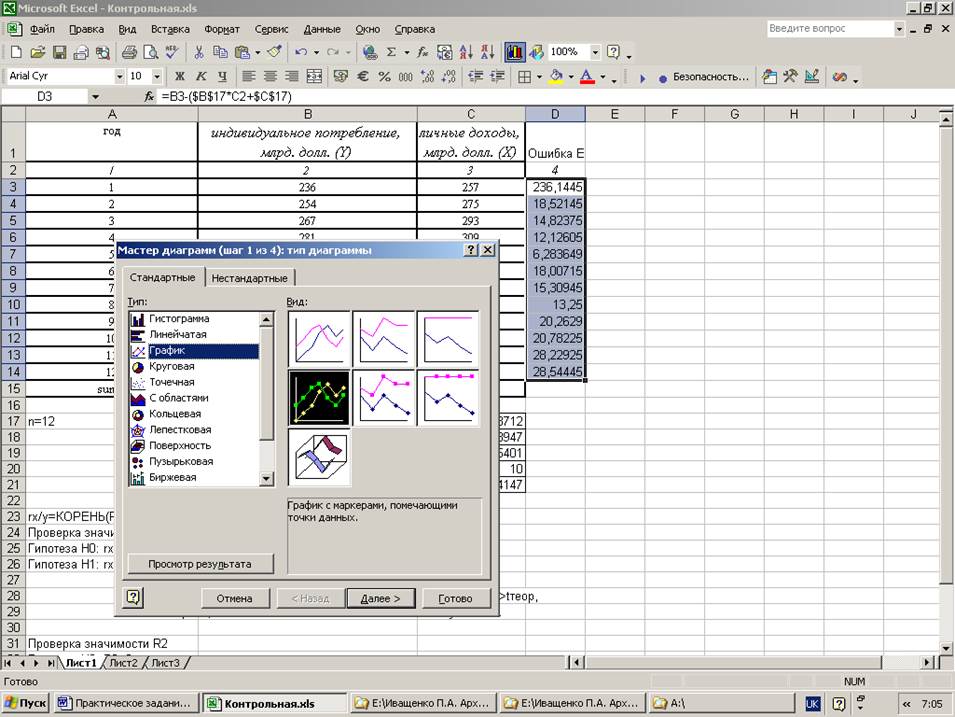
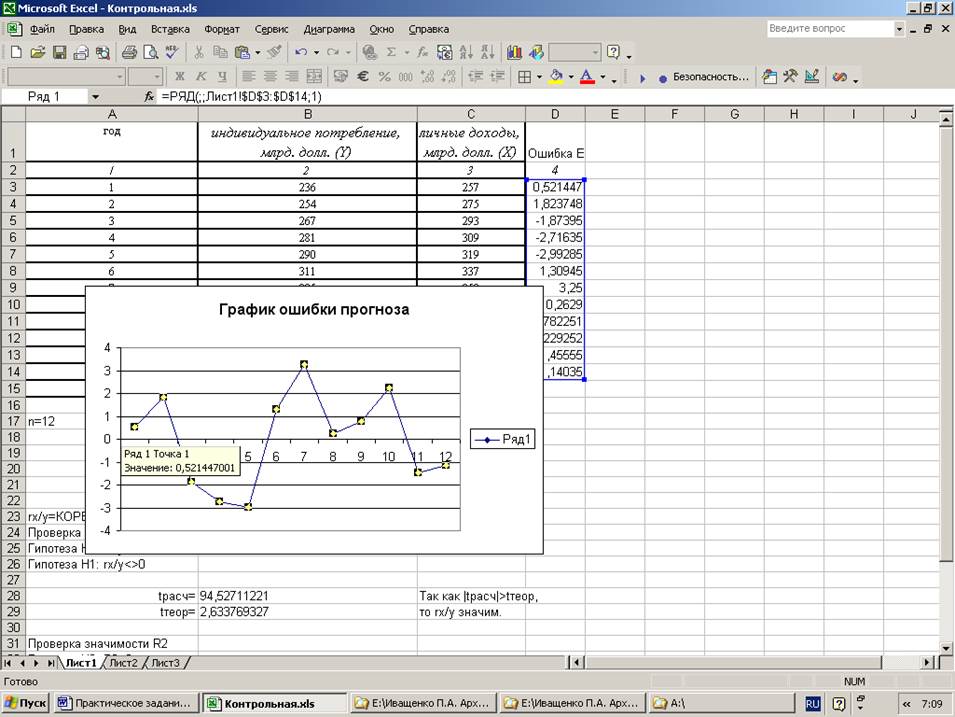
3. построить график ошибки прогноза.
Решение
Практическая работа № 2
Имеются следующие данные по 10 однотипным торговым предприятиям (Y -товарооборот, тыс. грн.; X - торговая площадь, м2):
|
№ п/п |
Y |
X |
|
1 |
560,5 |
268,4 |
|
2 |
630,5 |
317,9 |
|
3 |
754,9 |
369,5 |
|
4 |
839,1 |
423,5 |
|
5 |
967,5 |
478,3 |
|
6 |
1075,3 |
531,6 |
|
7 |
1121,3 |
583,2 |
|
8 |
1278,9 |
630,5 |
|
9 |
1370,6 |
676,2 |
|
10 |
1421,3 |
726,9 |
|
итого |
10019,9 |
5006,0 |
С помощью коэффициента корреляции оценить степень зависимости между товарооборотом и торговой площадью предприятия.
С помощью t-критерия с вероятностью 0,95 проверить существенность корреляционной связи.
Найти оценки параметров а и b и построить уравнение регрессии, дать экономическую интерпретацию полученных коэффициентов.
Рассчитать прогнозное значение товарооборота, если известно, что торговая площадь составит 750 м2. Построить график товарооборота с учетом прогнозного значения.
Решение
rx/y = 0,997402
Практическая работа № 4
Исследуется зависимость между стоимостью грузовой автомобильной перевозки Y (тыс. грн.), весом груза X1 (тонн) и расстоянием Х2 (тыс. км) по двадцати транспортным компаниям. Исходные данные приведены в таблице 4.1.
Таблица 4.1.
|
№ п/п |
Y |
X1 |
X2 |
|
1 |
51,0 |
35,0 |
2,00 |
|
2 |
16,0 |
16,0 |
1,10 |
|
3 |
74,0 |
18,0 |
2,55 |
|
4 |
7,5 |
2,0 |
1,70 |
|
5 |
33,0 |
14,0 |
2,40 |
|
6 |
26,0 |
33,0 |
1,55 |
|
7 |
11,5 |
20,0 |
0,60 |
|
8 |
52,0 |
25,0 |
2,30 |
|
9 |
15,8 |
13,0 |
1,40 |
|
10 |
8,0 |
2,0 |
2,10 |
|
11 |
26,0 |
21,0 |
1,30 |
|
12 |
6,0 |
11,0 |
0,35 |
|
13 |
5,8 |
3,0 |
1,65 |
|
14 |
13,8 |
3,5 |
2,90 |
|
15 |
6,2 |
2,8 |
0,75 |
|
16 |
7,9 |
17,0 |
0,60 |
|
17 |
5,4 |
3,4 |
0,90 |
|
18 |
56,0 |
24,0 |
2,50 |
|
19 |
25,5 |
9,0 |
2,20 |
|
20 |
7,1 |
4,5 |
0,95 |
|
итого |
454,5 |
277,2 |
31,8 |
По приведенным данным необходимо:
1) Построить уравнение регрессии;
2)
Рассчитать парные и частные
коэффициенты корреляции; проверить их
статистическую значимость;
3)
Построить уравнение регрессии в
стандартизированном виде, дать экономическую
интерпретацию полученного уравнения;
4) Построить график остатков;
5)
По уравнению регрессии рассчитать стоимость
грузоперевозки, если вес груза
составит 27 тонн, а расстояние 1,48 тыс. км
|
Q |
L |
К |
Ln Q (Y) |
Ln L (X1 |
Ln К (Х2 |
Y^2 |
Х1^2 |
Х2^2 |
|
657,29 |
162,31 |
279,99 |
||||||
|
935,93 |
214,43 |
542,5 |
||||||
|
1110,65 |
186,44 |
721,51 |
||||||
|
1200,89 |
245,83 |
1167,7 |
||||||
|
1052,68 |
211,4 |
811,77 |
||||||
|
3406,02 |
690,61 |
4558 |
||||||
|
2427,46 |
452,79 |
3069,9 |
||||||
|
4257,46 |
714,2 |
5585 |
||||||
|
1625,19 |
320,54 |
1618,8 |
||||||
|
1272,05 |
253,17 |
1562,1 |
||||||
|
1004,45 |
236,44 |
662,04 |
||||||
|
598,87 |
140,73 |
875,37 |
||||||
|
853,1 |
145,04 |
1697 |
||||||
|
1165,63 |
240,27 |
1078,8 |
||||||
|
1917,55 |
536,73 |
2109,3 |
||||||
|
9849,17 |
1564,8 |
13990 |
||||||
|
1088,27 |
214,62 |
884,24 |
||||||
|
8095,63 |
1083,1 |
9119,7 |
||||||
|
3175,39 |
521,74 |
5687 |
||||||
|
1653,38 |
304,85 |
1701,1 |
||||||
|
5159,31 |
835,69 |
5206,4 |
||||||
|
3378,4 |
284 |
3288,7 |
||||||
|
592,85 |
150,77 |
357,32 |
||||||
|
1601,98 |
259,91 |
2031,9 |
||||||
|
2065,85 |
497,6 |
2493 |
||||||
|
2293,87 |
275,2 |
1711,7 |
||||||
|
745,67 |
137 |
768,59 |
200,98 155,62 201,04
Исследуется зависимость между выпуском Q (млн.$) и затратами труда L (чел.) и капитала К (млн.$) в металлургической промышленности по 27 американским предприятиям.
Модель зависимости между выпуском и затратами труда и капитала, как правило, специфицируется
в виде производственной функции, чаще всего Кобба-Дугласа Q=A*L^b1*K^b2*e.
Поскольку модель является нелинейной, необходимо преобразовать ее к виду линейной по параметрам.
Для этого возьмем логарифм от обеих частей в уравнении:
lnQ=lnA+b1lnL+b2lnK+lne
Переобозначим для удобства: Y=lnQ, b0=lnA, X1=lnL, X2=lnK, u=Lne, тогда имеем линейную модель вида Y=b0+b1X1+b2X2+u
Доп. информация: А=е^1,11=3,03
необходимо:
1) найти b0,b1,b2.
2) построить уравнение регрессии в стандартизированном виде.
3) заполнить таблицу дисперсионного анализа (см. конспект)
4) проверить качество модели множественной регрессии с помощью F-критерия Фишера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.