Расчет абсолютной энтропии химических соединений в различных агрегатных состояниях. Вариант 37

Министерство образования Российской Федерации

Российский Государственный Университет

нефти и газа имени И.М. Губкина

Задание №1

Расчет абсолютной энтропиихимических соединений в различных агрегатных состояниях.

Вариант 37.

Кафедра физической и каллойдной химии.

Выполнил студент гр. ХТ-04-3

Молоканов А.А.

Проверил: Стыценко В.Д.

Москва

2006

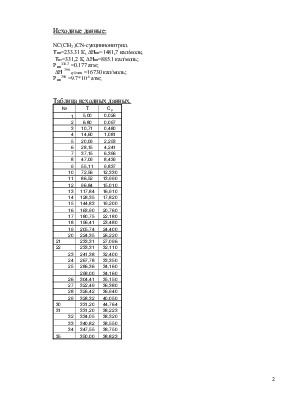
Исходные данные:

NC(CH₂ )CN-сукциннонитрил.

Т_пп=233.31 К, ∆Н_пп=1481,7 кал/моль;

 Т_пл=331,2 К, ∆Н_пп=885.1 кал/моль;

Р_нп^331.2 =0.177 атм;

 ∆Н ²⁹⁸ _сублим  =16730 кал/моль;

Р_нп²⁹⁸ =9.7*10^-6 атм;

Таблица исходных данных.                

№	T	Cp
1	5,00	0,026
2	6,80	0,097
3	10,71	0,480
4	14,60	1,081
5	20,09	2,253
6	28,15	4,241
7	37,15	6,396
8	47,09	8,439
9	55,11	9,837
10	72,56	12,330
11	86,52	13,990
12	96,84	15,010
13	117,84	16,910
14	128,35	17,820
15	144,83	19,200
16	163,90	20,760
17	180,75	22,180
18	196,41	23,480
19	205,74	24,400
20	224,35	26,220
21	233,31	27,096
22	233,31	32,110
23	241,38	32,400
24	267,78	33,350
25	286,36	34,160
	298,00	34,160
26	304,41	35,150
27	322,49	36,380
28	326,42	36,940
29	328,32	40,050
30	331,20	44,764
31	331,20	38,223
32	334,05	38,320
33	340,82	38,550
34	347,55	38,750
35	350,00	38,823

Задание:

Вычислите абсолютную энтропию сукцинонитрила в жидком состоянии при температуре 350 С .

Решение:

Для нахождения энтропии мы будим использовать следующую формулу:

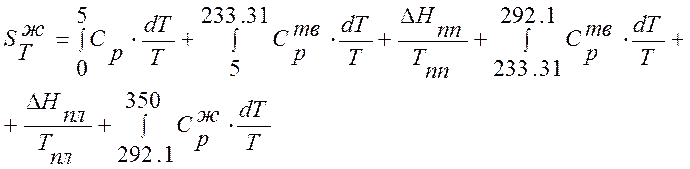
Величину первого интеграла определяют, используя уравнение зависимости теплоемкости твердых кристаллических тел вблизи абсолютного нуля  С_p=aT³

0,0026=a*5,00³

a=0,000208

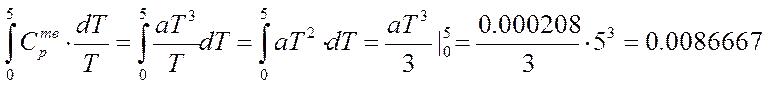
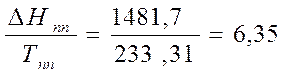 кал/моль*К  

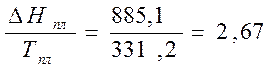 кал/моль*К 

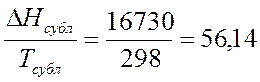 кал/моль*К 

Интегралы 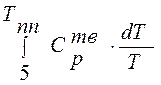;;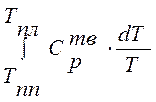  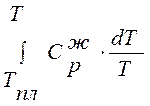,    ,    определяются графически, строя зависимость Ср/T от Т  – вычисляют по методу прямоугольной трапеции.

Определяем методом экстраполяции теплоемкости при температурах фазовых переходов и Т=350.

1. Т_пп=233,31К

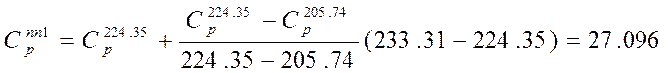кал/моль*К

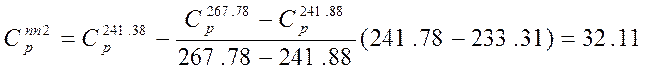кал/мольК

2. Т_пл=292,1 К

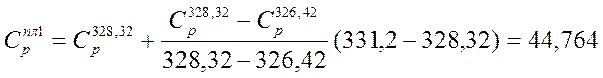 кал/моль*К

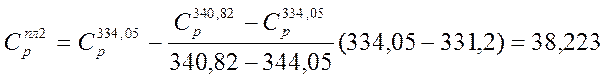 кал/моль*К

3. Т=350 К.

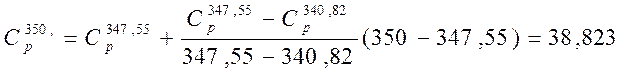 кал/моль*К

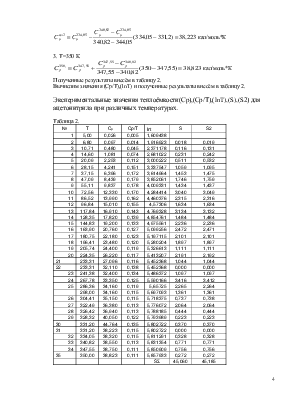
Полученные результаты внесём в таблицу 2.

Вычислим значения (Ср/Т),(lnT) и полученные результаты внесём в таблицу 2.

Экспериментальные значения теплоёмкости(Ср),(Ср/Т),(lnT),(S),(S2) для ацетонитрила при различных температурах.

Таблица 2.

№	T	Cp	Cp/T	lnt	S	S2
1	5,00	0,026	0,005	1,609438
2	6,80	0,097	0,014	1,916923	0,018	0,019
3	10,71	0,480	0,045	2,371178	0,116	0,131
4	14,60	1,081	0,074	2,681022	0,231	0,242
5	20,09	2,253	0,112	3,000222	0,511	0,532
6	28,15	4,241	0,151	3,337547	1,059	1,095
7	37,15	6,396	0,172	3,614964	1,453	1,475
8	47,09	8,439	0,179	3,852061	1,746	1,759
9	55,11	9,837	0,178	4,009331	1,434	1,437
10	72,56	12,330	0,170	4,284414	3,040	3,049
11	86,52	13,990	0,162	4,460376	2,315	2,316
12	96,84	15,010	0,155	4,57306	1,634	1,634
13	117,84	16,910	0,143	4,769328	3,134	3,132
14	128,35	17,820	0,139	4,854761	1,484	1,484
15	144,83	19,200	0,133	4,975561	2,236	2,236
16	163,90	20,760	0,127	5,099256	2,472	2,471
17	180,75	22,180	0,123	5,197115	2,101	2,101
18	196,41	23,480	0,120	5,280204	1,897	1,897
19	205,74	24,400	0,119	5,326613	1,111	1,111
20	224,35	26,220	0,117	5,413207	2,191	2,192
21	233,31	27,096	0,116	5,452368	1,044	1,044
22	233,31	32,110	0,138	5,452368	0,000	0,000
23	241,38	32,400	0,134	5,486372	1,097	1,097
24	267,78	33,350	0,125	5,590166	3,416	3,412
25	286,36	34,160	0,119	5,65725	2,265	2,264
	298,00	34,160	0,115	5,697093	1,361	1,361
26	304,41	35,150	0,115	5,718375	0,737	0,738
27	322,49	36,380	0,113	5,776072	2,064	2,064
28	326,42	36,940	0,113	5,788185	0,444	0,444
29	328,32	40,050	0,122	5,793989	0,223	0,223
30	331,20	44,764	0,135	5,802722	0,370	0,370
31	331,20	38,223	0,115	5,802722	0,000	0,000
32	334,05	38,320	0,115	5,811291	0,328	0,328
33	340,82	38,550	0,113	5,831354	0,771	0,771
34	347,55	38,750	0,111	5,850909	0,756	0,756
35	350,00	38,823	0,111	5,857933	0,272	0,272
				SΣ	45,060	45,185

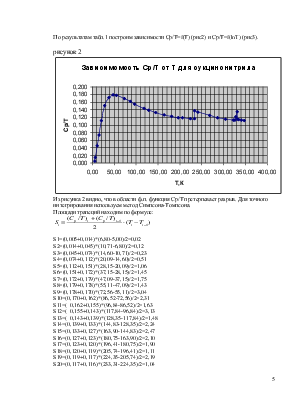
По результатам табл.1 построим зависимости Ср/Т=f(Т) (рис2) и Ср/Т=f(lnT) (рис3).

рисунок 2

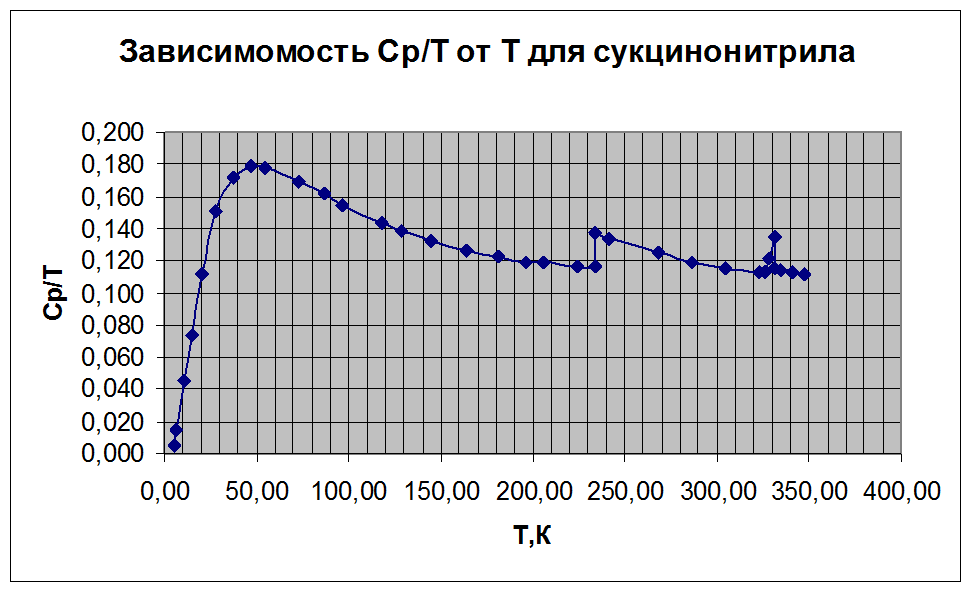
Из рисунка 2 видно, что в области ф.п. функция Ср/Т претерпевает разрыв. Для точного интегрирования используем метод Симпсона-Томпсона.

Площади трапеций находим по формуле:

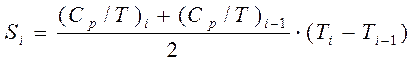
S1=(0,005+0,014)*(6,80-5,00)/2=0,02

S2=(0,014+0,045)*(10,71-6,80)/2=0,12

S3=(0,045+0,074)*(14,60-10,71)/2=0,23

S4=(0,074+0,112)*(20,09-14,60)/2=0,51

S5=(0,112+0,151)*(28,15-20,09)/2=1,06

S6=(0,151+0,172)*(37,15-28,15)/2=1,45

S7=(0,172+0,179)*(47,09-37,15)/2=1,75

S8=(0,179+0,178)*(55,11-47,09)/2=1,43

S9=(0,178+0,170)*(72,56-55,11)/2=3,04

S10=(0,170+0,162)*(86,52-72,56)/2=2,31

S11=(  0,162+0,155)*(96,84-86,52)/2=1,63

S12=(  0,155+0,143)*(117,84-96,84)/2=3,13

S13=(  0,143+0,139)*(128,35-117,84)/2=1,48

S14=(0,139+0,133)*(144,83-128,35)/2=2,24

S15=(0,133+0,127)*(163,90-144,83)/2=2,47

S16=(0,127+0,123)*(180,75-163,90)/2=2,10

S17=(0,123+0,120)*(196,41-180,75)/2=1,90

S18=(0,120+0,119)*(205,74-196,41)/2=1,11

S19=(0,119+0,117)*(224,35-205,74)/2=2,19

S20=(0,117+0,116)*(233,31-224,35)/2=1,04

S21=(0,116+0,138)*(233,31-233,31)/2=0,00

S22=(0,138+0,134)*(241,38-233,31)/2=1,10

S23=(0,134+0,125)*(267,78-241,38)/2=3,42

S24=(0,125+0,119)*(286,36-267,78)/2=2,27

S25=(0,119+0,115)*(304,41-286,36)/2=2,12

S26=(0,115+0,113)*(322,49-304,41)/2=2,06

S27=(0,113+0,113)*(326,42-322,49)/2=0,44

S28=(0,113+0,122)*(328,32-326,42)/2=0,22

S29=(0,122+0,135)*(331,20-328,32)/2=0,37

S30=(0,135+0,115)*(331,20-331,20)/2=0,00

S31=(0,115+0,115)*(334,05-331,20)/2=0,33

S32=(0,115+0,113)*(340,82-334,05)/2=0,77

S33=(0,113+0,111)*(347,55-340,82)/2=0,76

S34=(0,111+0,111)*(350,00-347,55)/2=0,27

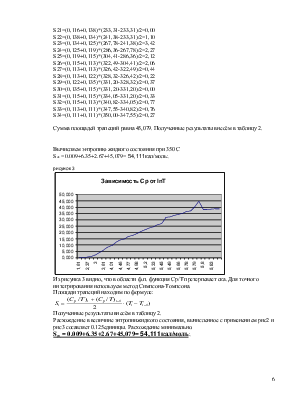
Сумма площадей трапеций равна 45,079. Полученные результаты внесём в таблицу 2.

Вычисляем энтропию жидкого состояния при 350 С

S_ж = 0.009+6.35+2.67+45,079= 54,111кал/моль;

рисунок 3

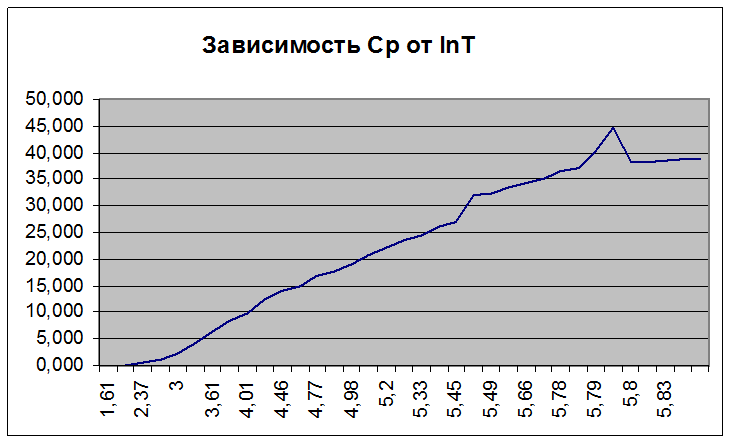
Из рисунка 3 видно, что в области ф.п. функция Ср/Т претерпевает ска. Для точного интегрирования используем метод Симпсона-Томпсона.

Площади трапеций находим по формуле:

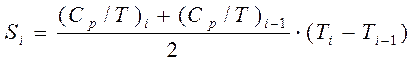
Полученные результаты внесём в таблицу 2.

Расхождение в величине энтропиижидкого состояния, вычисленное с применением рис2 и рис3 сосавляет 0.125единицы. Расхождение минимально.

S_ж = 0.009+6.35+2.67+45,079= 54,111кал/моль;