Проектирование железобетонного моста, страница 4

          р_n2=77,14 кН/м ,

          р_n3=88,17 кН/м ,

          р_n4=106,29 кН/м.

Нормативная  временная нагрузка умножается при расчёте на прочность на коэффициент надёжности по нагрузке g_fn , который принимает значения в зависимости от длины загружения линии влияния l:

          g_fn1=1,22 ,

          g_fn2=1,22 ,

          g_fn3=1,22 ,

          g_fn4=1,26.

Динамический коэффициент к нагрузкам от подвижного состава определяется по формуле

          1+m=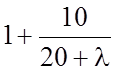=1+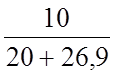=1,23.

Полные усилия в сечениях разрезной балки при расчёте на прочность определятся по следующим формулам:

М₁===12584,88 кНм;

М₂===16039,50 кНм;

Q₀===2604,09 кН;

Q₂===544,89 кН.

Усилия при расчёте на трещиностойкость определяются  от действия на конструкцию нормативных нагрузок. Коэффициенты надёжности по нагрузке в вышеприведённых формулах принимаются g_f1=g_f2=g_fn=1,0; динамический коэффициент  1+m=1,0:

М₁===9304,93 кНм;

М₂===11905,03 кНм;

Q₀===1918,64 кН;

Q₂===357,4 кН.

2.2.2. Расчёт балки из предварительно напряжённого железобетона.

Расчёт на прочность по изгибающему моменту.

Расчёту подлежат балочные пролётные строения железнодорожных мостов из предварительно напряжённого железобетона ( типовой проект серии 3.501-81).

Действительную форму поперечного сечения приводим к расчётной форме (рис.3 ). Вычисляем приведённую (среднюю) толщину плиты при фактической ширине плиты b_f=2,09 м:

          h_f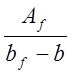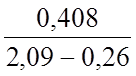^’===0,22 м.

Максимальная ширина плиты сжатой зоны тавровых и коробчатых сечений, учитываемая в расчёте, ограничена длиной свесов плиты, которая не должна быть больше 6h_f=1,32 м ; расчётная ширина плиты b_f^’ таврового сечения не должна превышать значения b_f^’  b+12h_f^’=2,90 м, а длина свесов плиты между соседними балками не должна быть больше

0,5(B-b)=0,5(1,80-0,26)=0,77 м, где

-B=1,80 м- расстояние между осями главных балок.

Действительная форма плиты переменной толщины и вутов заменяется в расчётном сечении прямоугольной формой  с толщиной h_f^’ и шириной b_f^’.

Центр тяжести арматуры ориентировочно назначается на расстоянии a_s=0,16 м от нижней грани пояса балки.

Расчёт на прочность по изгибающему моменту производим, начиная с наиболее нагруженного сечения. Определим в первом приближении высоту сжатой зоны бетона x₁ при действии расчётного момента М₂=16040 кН/м:

          x₁=h₀-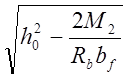=2,09-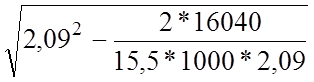=0,2521 м. Так как x₁=0,2521 м >h_f^’=0,22 м , то из этого следует, что в сжатую зону , кроме плиты, входит часть ребра главной балки, и сечение рассчитывается как тавровое. Расчётный изгибающий момент М₂ можно представить как сумму двух моментов: М₂^’ – воспринимаемый свесами  плиты, М₂^’’- воспринимаемый сжатой зоной ребра,

          М₂=М₂^’+M₂^’’.

Предельный момент, воспринимаемый свесами плиты A_f^’ и соответствующей частью рабочей арматуры, равен

          М₂^’=R_b(b_f^’-b)h_f^’(h₀-0,5h_f^’)=15,5*1000*(2,09-0,26)*0,22*(2,09-0,5*0,22)=12356 кНм.

По оставшейся части момента M₂^’’=М₂-М₂^’=16040-12356=3684 кНм находим высоту сжатой зоны в ребре:

x₁=h₀-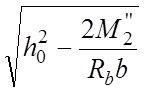=2,09-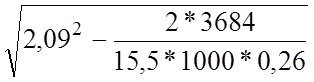= 0,4963 м.

Плечо пары внутренних сил таврового сечения

          z=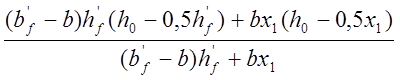==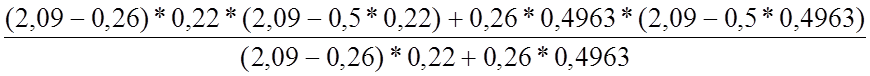1,946 м.

Определяем необходимую площадь рабочёй предварительно напряжённой арматуры:

          A_s=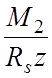==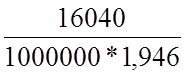8,242*10^-3 м²=82,42 см².

Армирование будем производить пучками высокопрочной проволоки класса В-11, пучками 42Æ5 c расчётным сопротивлением R_p=1000 МПа. Площадь поперечного сечения одной проволоки равна 0,196 см², площадь поперечного сечения пучка A_p1=8,23 см².Определяем необходимое количество пучков проволоки:

n_пуч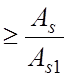==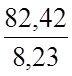10,01 шт, где

-n_пуч- целое число пучков;

-A_s1-площадь сечения одного стержня.

Принимаем количество пучков n_пуч=11.

Размещение пучков напрягаемой арматуры показано на рис.  

После уточнения площади A_p c учётом принятого количества пучков проволоки находим значение x₂:

          x₂=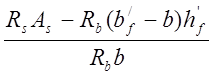==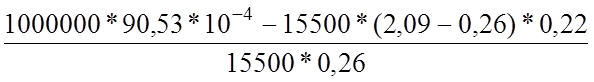0,6979 м.

Окончательное значение z вычисляем по вышеприведённой формуле с подстановкой x₂ вместо x₁:

z=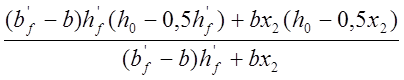==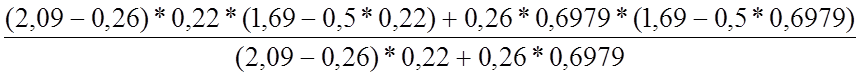1,5058 м.

Условие прочности сечения по изгибающему моменту записывается в виде

          М_пр=R_pA_sz³М₂

               М_пр=1000000*90,53*10^-4*1,5058=13632 кН³ М₂=16040 кН.

Проверка выполняется, расчёт сечения на прочность по изгибающему моменту закончен.   

 Расчёт на трещиностойкость в стадии изготовления и эксплуатации.

А. Проверка по образованию нормальных трещин  в стадии эксплуатации.

Расчёт производится по наибольшему изгибающему моменту  М^’’=11905,03 кНм от нормативных нагрузок. Предполагается, что на стадии образования трещин бетон и арматура сохраняют упругие свойства. Благодаря предварительному напряжению, конструкция работает полным сечением.

Расчётная форма сечения с основными размерами показана на рис.  

Принимаем способ натяжения арматуры – натяжение на упоры. При натяжении арматуры на упоры её сцёпление с бетоном обеспечивается до передачи на конструкцию предварительного натяжения. На всех стадиях изготовления и эксплуатации бетон и арматура в сечениях работают совместно. Определим геометрические характеристики приведённого сечения:

          А_b= А_b1+ А_b2+ А_b3=0,4598+0,4108+0,37=1,2406 м² - площадь бетонного сечения;

          S_b=A_b1(h-0,5h)+0,5 А_b2(h-h+h)+0,5 А_b3h=0,4598*(2,25-0,5*0,22)+0,5*0,4108*(2,25-0,22+0,45)+0,5*0,37*0,45=1,5766 м² – статический момент бетонного сечения относительно нижней грани балки;

          A_red= А_b+n₁A_p=1,2406+5,4*0,008232=1,285053 м² – приведённая (с учётом арматуры) площадь поперечного сечения.

          S_red=S_b+n₁A_pa_p=1,5766+5,4*0,008232*0,16=1,583712 м² – статический момент приведённого сечения относительно нижней грани.

          y_c,red=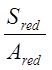 ==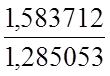1,23 м – расстояние до центра тяжести приведённого сечения от нижнеё грани.

          y=h-y=2,25-1,23=1,02 м  – расстояние до центра тяжести приведённого сечения от верхней грани.

                     I_red=+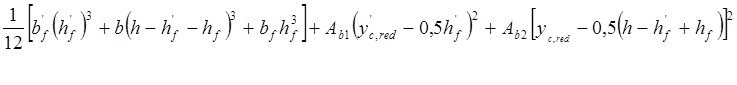

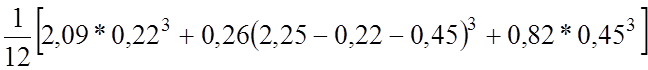   =++0,4108=0,90094 м⁴ – момент инерции приведённого сечения относительно нейтральной оси.

          W_red­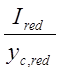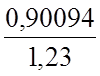===0,73105 м³ – момент сопротивления приведенного сечения относительно нижней грани сечения.

          Ожидаемые растягивающие напряжения у нижней грани

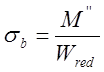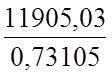          ==16284 кН/м²

Предельные растягивающие напряжения в бетоне