Таким образом, мы получили, что y1E = 2,4, а y2E = 0.
Отсюда:
с1Е = 120*2,4 + 0,4*0 = 288,
а самый большой доход исследуемой фирмы может составить:
ZmaxЕ = b1y1E + b2y2E = 3000*2,4 + 120*0 = 7200.
Уменьшение цены 1-го товара вызовет сдвиг отрезка АВ влево-вниз как на рис.3,б. В результате граница ОДР изменяется так, что т. В перемещается в т. L, при этом т. D остается без изменений (соответственно, оптимальный план и доходы остаются на прежнем уровне), а нижний предел 1-го типа товара – бесконечность.
С экономической точки зрения: исходная цена продажи 1-го товара слишком мала, чтобы компенсировать издержки на его закупку (это означает, что понижение цены просто нецелесообразно).
Проведем анализ изменения цен на все остальные виды товаров.
Пусть с2 увеличивается. Тогда прямая, соответствующая ограничению (2), а с ней и отрезок ВС будут сдвигаться вправо-вверх, от т. С к т. D. До этого момента роста доходов не будет, т.к. 2-й тип товара убыточен, и только когда цена его станет равной:
с2 D = 60y1D + 1,2y2D=60*0,9 + 1,2*25 = 84,
он начнет приносить прибыль до тех пор, пока т. D не совпадет с т. Е, что было рассмотрено выше.
В случае с2 – уменьшается, прямая ВС движется влево-вниз, при этом тт.В и С сойдутся в т. Н, но наши доходы останутся прежними, т.к. 2-й тип товара так же убыточен, как и первый, поэтому нижний предел в этом случае – бесконечность.
Пусть с3 – увеличивается. Тогда прямая СD движется вправо-вверх, а т. D к т. Е. Это сразу же скажется на доходах фирмы, которые будут расти вплоть до т. Е, где:
С3Е = 50y1Е + 1,8y2Е = 50*2,4 + 1,8*0 = 120.
(координаты точки Е и ZЕ найдены выше)
Если же с3 – уменьшается, прямая СD движется влево-вниз, а тт.С и D сойдутся в т. М, координаты которой найдем, решив систему:
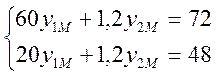
![]()
![]()
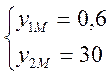
Тогда с3М = 50*0,6 + 1,8*30 = 84 и наши доходы упадут до ZМ = 5400
Пусть с4 -
увеличивается. Тогда прямая, соответствующая ограничению (4) двойственной
задачи, а с ней и отрезок DЕ будут сдвигаться вправо-вверх. При этом т. D
будет двигаться к т.С, потом к т. В, далее к т. А и так до бесконечности.
Доходы же фирмы будут постоянно расти, т.к. максимальная линия уровня будет все
дальше уходить от начала координат. Экономически это понятно, потому, что
товары 4-го типа были нам выгодны с самого начала. Найдем координаты т. С,
которая лежит на пересечении ограничений (2) и (3) двойственной задачи: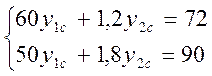
![]()
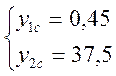
откуда найдем чему равен с4С :
с4с = 20*0,45 + 1,2*37,5 = 54, а
ZC = b1y1C + b2y2C = 3000*0,45 + 120*37,5 =5850
Если с4 – уменьшается, прямая DЕ движется влево-вниз, пока т. D не совпадет с т. М, координаты которой - (1,8;0) – видны на рис.1.Тогда:
с4М = 20y1М + 1,2y2М = 20*1,8 + 1,2*0 =36
ZМ = 3000y1М +120 y2М = 5400
Изменим значение цены на 5-ый вид товара. Если с5 - увеличивается, то прямая ОА движется влево, но доходы начнут расти только тогда, когда, двигаясь по границе ОДР, достигнет т. D. Это связано с тем, что 5-ый тип товара самый убыточный при исходных ценах. Когда же она станет равной:
с5D = 70y1D = 70*0,9 = 63,
доходы от его продажи начнут покрывать затраты на покупку, он будет приносить прибыль, до тех пор, пока хватит ресурсов, т.е. пока т. D не совпадет с т. Е, двигаясь по границе ОДР.
В случае же, когда с5 – уменьшается, это, как и для товаров 1-го и 2-го типов, никак не отразится на наших доходах, поскольку исходная цена слишком мала, чтобы обеспечить рентабельное производство (закупку и продажу).
Полученные результаты, сделанные на основе графического решения задачи, полностью подтверждаются алгебраическими вычислениями, выполненными в ПЭР:
┌──────────────────────────────────────────────────────────────────────────────┐
│ АНАЛИЗ УСТОЙЧИВОСТИ КОЭФФ. ЦЕЛЕВОЙ Ф-ЦИИ Стр. : 1 │
╞═════╤══════════╤══════════╤══════════╦═════╤══════════╤══════════╤═══════════╡
│C(j) │Min. C(j) │ Исходный │Max. C(j) ║C(j) │Min. C(j) │ Исходный │Max. C(j) │
╞═════╪══════════╪══════════╪══════════╬═════╪══════════╪══════════╪═══════════╡
│C(1) │- бесконеч│ 48.0000│ 118.0000║C(4) │ 36.0000│ 48.0000│ 54.0000 │
│C(2) │- бесконеч│ 72.0000│ 84.0000║C(5) │- бесконеч│ 14.0000│ 63.0000 │
│C(3) │ 84.0000│ 90.0000│ 120.0000║ │ │ │ │
└─────┴──────────┴──────────┴──────────╨─────┴──────────┴──────────┴───────────┘
На этом экономический анализ задачи линейного программирования можно считать законченным.
Вывод: научились понимать смысл, различать, осознанно использовать такие понятия как математическая модель ЗЛП, симметричная и каноническая формы записи ЗЛП, геометрическая интерпретация ЗЛП, двойственные задачи, двойственные оценки, устойчивость решения ЗЛП, устойчивость оценок. Получили навыки, научились строить математические модели ЗЛП, переходить от одной формы записи ЗЛП к другой, решать ЗЛП графически, строить модели двойственных задач, находить решение ЗЛП на основе решения задачи, двойственной к ней, интерпретировать полученные результаты в терминах решаемой задачи, проводить анализ устойчивости решения ЗЛП на основе геометрической интерпретации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.