где Z* - оптимальное значение, полученное из итоговой таблицы, а ΔZ – изменение целевой функции, найденное по формуле (***). Знак определяется направлением изменения: “+” - при увеличении запасов (Δb1 или Δb2) и “-“ - в противном случае.
Интервалы устойчивости можно найти чисто геометрически, пользуясь графическим решением задачи. Для того чтобы понять, что будет происходить на этом рисунке при изменении запасов ресурсов и как это повлияет на положение точки оптимума D, необходимо представить уравнение линии уровня в следующей форме:
Z0 = y1b1 + y2b2 ![]() y1
=
y1
= 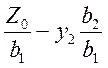 ,
(1)
,
(1)
где отношение ![]() показывает тангенс угла наклона
прямой,
показывает тангенс угла наклона
прямой,
соответствующей (1) к оси OY1. Рассмотрим теперь следующие случаи:
1) пусть b2 = const, b1 - ↑ (увеличивается), тогда тангенс уменьшается и угол наклона к оси OY1 также становится меньше;
2) пусть b2 = const, b1 - ↓ (уменьшается), тогда тангенс и угол, ему соответствующий, увеличиваются.
Линия уровня, проходящая
через точку D, «привязана» к ее координатам (![]() ,
,![]() ) так,
что при изменении b1 она
будет поворачиваться вокруг точки D как оси, причем при b1 - ↑ по часовой стрелке, а при b1 - ↓ - соответственно против. Все это схематично
показано на рис.2. Здесь цифрами указаны номера ограничений в двойственной
задаче, которые формируют соответствующую сторону многоугольника ОДР.
) так,
что при изменении b1 она
будет поворачиваться вокруг точки D как оси, причем при b1 - ↑ по часовой стрелке, а при b1 - ↓ - соответственно против. Все это схематично
показано на рис.2. Здесь цифрами указаны номера ограничений в двойственной
задаче, которые формируют соответствующую сторону многоугольника ОДР.
Таким образом, значение b1, при котором линия уровня совпадает с прямой 3 будет b1max , так как дальнейший рост b1 вызовет такой наклон линии уровня к оси OY1, что оптимальной станет уже точка C и
координаты (![]() ,
,![]() ) изменятся.
) изменятся.
Из аналитической геометрии известно, что, если две прямые параллельны (или совпадают), коэффициенты при соответствующих переменных в обоих уравнениях пропорциональны. Тогда при совпадении линии уровня
b1max y1 + 120y2 = Zmax
и прямой 3:
50y1 + 1,8y2 = 90,
имеет пропорцию:
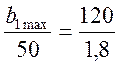 ,
,
откуда b1max = 3333,33, что полностью совпадает с решением, полученным нами ранее. Рассуждая точно так же в случае, когда b1 уменьшается, найдем, что условием совпадения линии уровня и прямой 4 является выполнение соотношения:
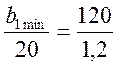 .
.
Тогда b1min = 2000, что также соответствует алгебраическому решению.
Пусть теперь изменяется b2, а b1=const. Очевидно, что эти изменения могут быть точно так же проиллюстрированы геометрически, как и для b1. Только в этом случае будет меняться наклон линии уровня к оси OY2. Тогда, при увеличении b2, линия уровня будет поворачиваться вокруг точки D против часовой стрелки, пока не совпадет с прямой 4, а это произойдет лишь при условии:
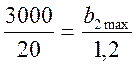
откуда b2max = 180. Аналогично, уменьшение b2 приведет к совпадению с прямой 3 при условии:
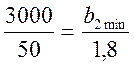
и b2min = 108. Эти результаты полностью совпадают с решением, найденным с помощью средств ПЭР.
Рассмотрим теперь вопрос о влиянии коэффициентов целевой функции на ее величину (как изменение цен на готовую продукцию влияет на доходы предприятия). Графическое решение этой задачи поможет сделать это особенно наглядно.
В модели двойственной задачи цены на товары сj находятся в правых частях ограничений двойственной задачи. Уравнение в общем виде:
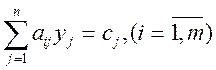 , (2)
, (2)
Уравнение (2) определяет соответствующую сторону многоугольника ОДР на рис. 1, 2.
Таким образом, изменения величины правой части в (2) приведут к сдвигу соответствующей стороны параллельно самой себе либо вправо-вверх, если сj растет, либо влево-вниз, если сj уменьшается. На рис.3 это схематично показано.
Катя, как ты поняла, рисунки я чертила от руки ( в сиреневой методичке все есть!)
При увеличении с1, отрезок АВ, который определяется первым ограничением двойственной задачи, будет двигаться вправо (рис.3,а). При этом в т.В будет сближаться с т.С, пока не сольется с ней и т.д., пока «новая граница» ОДР не подойдет к т.Dё До этого момента рост цены 1-го товара никак не сказывался на оптимальном плане закупок (и, соответственно, на величине Zmax ) т.к. это не влияло на координаты т.D. Дальнейший же рост этой цены приведет к тому, что т. D начнет двигаться по отрезку DЕ, пока не сольется с т.Е. Величина целевой функции в т. Е будет больше, чем в т. D, т.к. линия максимального уровня сместится при этом вправо, т.е. в сторону увеличения. Но дальше, на сколько бы мы ни поднимали цену, это не даст дополнительной прибыли, т.к. мы имеем ограниченные ресурсы.
Экономически эта ситуация объясняется тем, что в «исходном положении» продажа 1-го товара по цене с1 нерентабельна. И только тогда, когда эта цена вырастет настолько, что начнет покрывать все расходы, связанные с его закупкой (в т. D), 1-й товар начнет приносить прибыль.
Таким образом, ясно, что тт. D и Е являются «поворотными моментами» в деятельности данной коммерческой фирмы при увеличении с1. «Критическую» цену в т. D можно найти, подставив координаты в т. D (0,9;25) в уравнение:
с1кр = 120y1D + 0,4y2D = 120*0,9+0.4*25=118.
Цену 1-го
товара в т. Е можно также найти через координаты т. Е, которая находится на
пересечении ограничения (4) двойственной задачи и оси 0Y1. Решим
систему 2-х уравнений: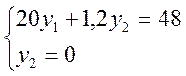
![]()
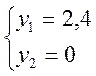
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.