Построение математической модели задач линейного программирования. Вариант № 9

МО и ПО РФ Новосибирский Государственный Технический Университет Кафедра экономической информатики Расчетно-графическая работа по курсу «Теория оптимального управления в экономических системах» Вариант 9 Факультет: Бизнеса Группа: Студент: Преподаватель: Новосибирск 2003

Цели задания

1. Понимать смысл, различать, осознанно использовать следующие понятия: математическая модель ЗЛП; симметричная и каноническая формы записи ЗЛП; геометрическая интерпретация ЗЛП; двойственные задачи; двойственные оценки; устойчивость решения ЗЛП; устойчи­вость оценок.

2. Получить навыки, уметь: строить математические модели ЗЛП; переходить от одной формы записи ЗЛП к другой; решать ЗЛП графи­чески; строить модели двойственных задач; находить решение ЗЛП на основе решения задачи, двойственной к ней; интерпретировать полу­ченные результаты в терминах решаемой задачи; проводить анализ ус­тойчивости решения ЗЛП на основе геометрической интерпретации.

Условие задачи

     Коммерческая фирма предполагает осуществить оптовую закупку продовольствия, располагая для этого суммой Sмлн. руб. Номенкла­тура продовольствия включает пять наименований: ai, А2, а3, А4 и А5. Покупная цена каждого продукта равна соответственно S₁, s₂, s₃, s₄ и s₅ тыс.руб./кг. В распоряжении фирмы имеются холодильные камеры общей площадью V м² Площадь, необходимая для хранения одно­го кг продукта каждого вида, равна соответственно v₁, v₂, v₃, v₄ м²; при этом продукт a5 хранению не подлежит и должен быть реализован немедленно. При своевременной реализации продуктов каждого вида прибыль составит соответственно p1,р2, Р3, Р4 и p5 тыс.руб./кг.

Определить объемы закупки продовольствия, при которых фирма может рассчитывать на максимальную прибыль.

Исходные данные

N	S	V
9	3	120	120	60	50	20	70	0,40	1,20	1,80	1,20	48	72	90	48	14

Задание

     Записать математическую модель задачи. Решить задачу графичес­ки, для чего построить модель задачи, двойственной к заданной, и дать ее геометрическую интерпретацию. Используя результат графи­ческого решения двойственной задачи, найти решение исходной. Дать экономическую интерпретацию двойственным оценкам. Произвести ана­лиз устойчивости полученного решения и оценок на основе геометри­ческой интерпретации двойственной задачи.

     Решить задачу на ПЭВМ с помощью Пакета Экономических Расчетов (ПЭР) и сравнить результаты с полученными ручным способом.

Решение: построим сначала математическую модель прямой задачи. Переменными здесь являются реализованные объемы продуктов каждого вида: х₁-объем продукта 1-го вида, х₂,х₃,х₄,х₅ – объемы продуктов 2-го,3-го,4-го и 5-го видов соответственно.

    Целевая функция задачи – общая прибыль – будет  складываться из сумм, полученных от реализации объемов каждого вида продуктов, поэтому:

Z() = 48x₁+72x₂+90x₃+48x₄+14x₅max.

    Достижение этой цели будет ограничиваться запасами имеющихся ресурсов:

- деньгами, выделенными для закупки необходимых объемов:

                                120x₁+60x₂+50x₃+20x₄+70x₅3000;                                    (*)

- площадями холодильников для хранения необходимых объемов:

                                  0,4x₁+1,2x₂+1,8x₃+1,2x₄120.                                               (**)

х₅ не входит в последнее равенство, т.к. по условию задачи продукт А₅ хранению не подлежит.

     Переменные задачи должны удовлетворять соотношениям:

х_j0, (j=)

   Модель прямой задачи имеет только два ограничения, поэтому модель двойственной задачи будет содержать только две переменные:

              Ограничения:1)120y₁ + 0,4y₂  48,

                           2)60y₁ + 1,2y₂  72,

                            3)50y₁ + 1,8y₂  90,

                           4)20y₁ + 1,2y₂  48,

                           5)70y₁ + 0y₂  14,

                                 y₁, y₂ 0.

     Двойственную задачу решим графически, на плоскости у₁0у₂ (рис.1) Цифрами обозначены линии, определяющие полуплоскость соответствующего неравенства.

                         Здесь должен быть рисунок 1 (в сиреневой методичке аналогичный), просто я решила не чертить в WORDE, а начертила на миллимитровке.

     Как видно из графика (рис.1.), мы получили 4 угловых точки (A,B,C,D). Подставляя координаты каждой точки в уравнение целевой функции двойственной задачи, определим, где  находится оптимальный план задачи.

       А(0,2;60):  3000*0,2+ 120*60 = 7800;

В(0,24;48):  3000*0,24 + 120*48 = 6480;

С(0,45;37,5):  3000*0,45 + 120*37,5 = 5850;

D(0,9;25):  3000*0,9 +120*25 = 5700.

     Так как в точке D значение целевой функции минимальное, значит, оптимальный план задачи находится в этой точке, координатами  которой  будут: Y*, при этом

     С помощью второй теоремы двойственности найдем решение прямой задачи:

    

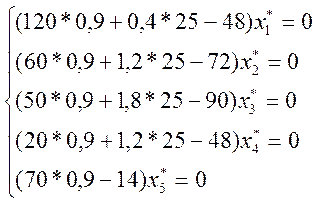
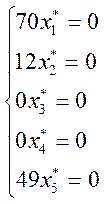
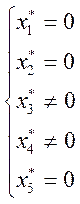
Таким образом, в плане * прямой задачи только координаты   и  отличны от нуля. Согласно 2-ой теореме двойственности и  должны удовлетворять следующим соотношениям:

(50*+20*-3000)=0

(1,8*+1,2-120) =0

Поскольку >0 и >0, то:

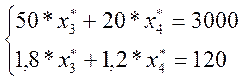
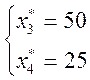
Соответственно, решение исходной задачи *=(0,0,50,25,0) и

     Решим теперь обе задачи алгебраически с помощью ПЭР. Вводя исходные данные, получаем следующую таблицу:

                         ВХОДНЫЕ ДАННЫЕ,  описывающие задачу  РГР9   Стр.  1

Max  +48.0000X1  +72.0000X2  +90.0000X3  +48.0000X4  +14.0000X5

При огран.

( 1) +120.000X1  +60.0000X2  +50.0000X3  +20.0000X4  +70.0000X5  є +3000.00

( 2) +.400000X1  +1.20000X2  +1.80000X3  +1.20000X4  ________X5  є +120.000

    Далее решаем задачу симплекс-методом и получаем следующие таблицы:

НАЧАЛЬН.ТАБЛИЦА

  ┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬──────┐

  │     │     │X1   │X2   │X3   │X4   │X5   │S1   │S2   │     │ B(i) │

  │     │     ├─────┼─────┼─────┼─────┼─────┼─────┼─────┤     │──────│

  │Базис│C(j) │48.00│72.00│90.00│48.00│14.00│    0│    0│B(i) │A(i,j)│

  ╞═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪══════╡

  │S1   │    0│120.0│60.00│50.00│20.00│70.00│1.000│    0│ 3000│    0 │

  │     │     │     │     │     │     │     │     │     │     │      │

  │S2   │    0│0.400│1.200│1.800│1.200│    0│    0│1.000│120.0│    0 │

  ╞═════╧═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪══════╡

  │ C(j)-Z(j) │48.00│72.00│90.00│48.00│14.00│    0│    0│    0│      │

  │   * Big M │    0│    0│    0│    0│    0│    0│    0│    0│      │

  └───────────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴──────┘

КОНЕЧНАЯ ТАБЛИЦА (Всего итерац.=  2 )

   ┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬──────┐

   │     │     │X1   │X2   │X3   │X4   │X5   │S1   │S2   │     │ B(i) │

   │     │     ├─────┼─────┼─────┼─────┼─────┼─────┼─────┤     │──────│

   │Базис│C(j) │48.00│72.00│90.00│48.00│14.00│    0│    0│B(i) │A(i,j)│

   ╞═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪══════╡

   │X3   │90.00│5.667│2.000│1.000│    0│3.500│0.050│-.833│50.00│    0 │

   │     │     │     │     │     │     │     │     │     │     │      │

   │X4   │48.00│-8.17│-2.00│0.000│1.000│-5.25│-.075│2.083│25.00│    0 │

   ╞═════╧═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪═════╪══════╡

   │ C(j)-Z(j) │-70.0│-12.0│    0│    0│-49.0│-.900│-25.0│ 5700│      │

   │   * Big M │    0│    0│    0│    0│    0│    0│    0│    0│      │

   └───────────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────

   ┌─────────────────────────────────────────────────────────────────┐