Построение математической модели задач линейного программирования. Вариант № 9, страница 2

   │                  ИТОГОВЫЙ РЕЗУЛЬТАТ ДЛЯ РГР9    Стр. : 1        │

   ╞═════════╤══════════╤═══════════╦═════════╤══════════╤═══════════╡

   │Переменн.│          │Двойственн.║Переменн.│          │Двойственн.│

   │No. Имена│ РЕШЕНИЕ  │   оцен    ║No. Имена│ РЕШЕНИЕ  │   оцен    │

   ╞═════════╪══════════╪═══════════╬═════════╪══════════╪═══════════╡

   │1   X1   │    0.0000│   70.0000 ║5   X5   │    0.0000│   49.0000 │

   │2   X2   │    0.0000│   12.0000 ║6   S1   │    0.0000│    0.9000 │

   │3   X3   │   50.0000│    0.0000 ║7   S2   │    0.0000│   25.0000 │

   │4   X4   │   25.0000│    0.0000 ║         │          │           │

   ╞═════════╧══════════╧═══════════╩═════════╧══════════╧═══════════╡

   │            MAX   величина цел.ф-и = 5700  Итерац.= 2            │

   └─────────────────────────────────────────────────────────────────┘

     Как видно из таблиц, графическое и алгебраическое (с помощью ПЭР) решения полностью совпадают.

     Проведем экономический анализ полученного решения. Для этого выпишем все переменные (как основные, так и дополнительные) прямой задачи:

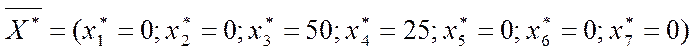
и, пользуясь таблицей соответствия и конечной симплекс-таблицей решенной задачи, также все переменные двойственной задачи:

 = (=0,9; =25; =70; =12; =0; =0; =49).

     Величины  и  показывают, что товары 3-го типа необходимо закупить в количестве 50 шт., а товаров 4-го типа – 25 шт. Товары же 1-го, 2-го и 5-го типов нецелесообразно закупать вообще. Двойственные оценки ,  и  это подтверждают.

Действительно, двойственные переменные являются мерой убыточности производства соответствующего типа продукции, следовательно, величина

 = 70 говорит о том, что стоимость ресурсов, расходуемых на производство (закупку) 1 ед. товара 1-го типа в оптимальных ценах (т.е. фактически наши затраты), превосходит цену этого товара (т.е. наши доходы) на 70 единиц в стоимостном выражении. Это следует из первого ограничения двойственной задачи:

 = a₁₁+a₂₁–c₁ = 120*0,9  +  0,4*25  –  48  =  70.

Точно так же значения  и  показывают нам степень нерентабельности производства (закупки) товаров 4-го и 7-го типов. Второе и пятое ограничения двойственной задачи доказывают это:

 = a₁₂ + a₂₂ – c₂ = 60*0,9  +  1,2*25  –  72  =  12.

=a₁₅ + a₂₅  – с₅ = 70*0,9 – 14 = 49.

Из последних выражений следует (сравнив правые части), что товар 1-го типа является самым “невыгодным”, т.к. его закупка обходится дороже всего.

Теперь обратимся к дополнительным переменным прямой задачи. Их значения показывают остатки соответствующего вида ресурса после выполнения оптимального плана. Таким образом, величина  говорит, что 1-й ресурс – деньги – будет израсходован полностью. Действительно, из первого ограничения прямой задачи (*) следует:

 = 120+60+50+20+70-3000 = 50*50 + 20*25 -3000 =0;

         То же самое можно сказать про остатки 2-го ресурса – площади холодильников – их не будет, так как из второго ограничения прямой задачи (**) очевидно, что:

 = 0,4+1,2+1,8+1,2-120 = 1,8*50 + 1,2*25 – 120 = 0

  Двойственные оценки  и , которые показывают степень использования соответствующего ресурса, подтверждают это, так как их значения больше нуля. Тогда изменения обоих видов ресурсов (как увеличение, так и уменьшение) должны приводить к такому же изменению общего дохода, т.е. целевой функции, как это следует из 3-й теоремы двойственности. Для нашей задачи она запишется так:

                          ΔZ≈ yΔb₁  + Δb₂ = 0,9*Δb₁  + 25* Δb₂                     (***)

Таким образом, изменение 1-го ресурса на единицу ведет к такому же изменению (увеличению/уменьшению) дохода на 0,9 ед., а 2-го ресурса – на 40 ед. в стоимостном выражении.

Но, здесь необходимо заметить, что последняя формула имеет смысл тогда, когда Δb₁ и Δb₂ изменяются в пределах интервалов устойчивости. Для их определения воспользуемся ПЭР:

 ┌──────────────────────────────────────────────────────────────────────────────┐

 │                        АНАЛИЗ УСТОЙЧИВОСТИ ПР.ЧАСТИ       Стр. : 1           │

 ╞═════╤══════════╤══════════╤══════════╦═════╤══════════╤══════════╤═══════════╡

 │B(i) │Min. B(i) │ Исходный │Max. B(i) ║B(i) │Min. B(i) │ Исходный │Max. B(i)  │

 ╞═════╪══════════╪══════════╪══════════╬═════╪══════════╪══════════╪═══════════╡

 │B(1) │ 2000.0000│ 3000.0000│ 3333.3335║B(2) │  108.0000│  120.0000│  180.0000 │

 └─────┴──────────┴──────────┴──────────╨─────┴──────────┴──────────┴───────────┘

     Исходные значения ресурсов нашей задачи b₁=3000, а b₂=120. Тогда:

=

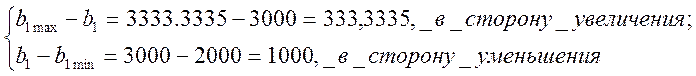
и

=

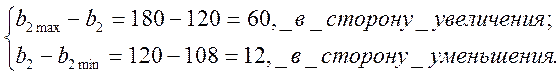
      Убедимся в правильности определения интервалов устойчивости оценок без использования средств ПЭР:

Ø По сумме на закупку продовольствия:

 

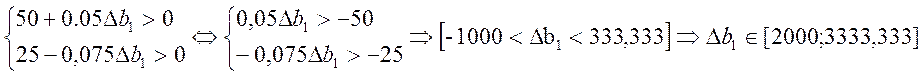
Ø По площади, необходимой для хранения продуктов:

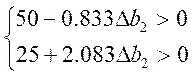
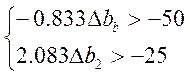
     Таким образом, интервалы устойчивости оценок по отношению к ограничениям по видам ресурсов как без использования средств ПЭР, так и при помощи средств ПЭР совпадает. Тем самым мы имеем, что оптимальный план будет устойчивым лишь в том случае, когда значения наших ресурсов ( и ) не будут превышать найденных интервалов устойчивости.

      Таким образом, если запасы обоих ресурсов изменяются в указанных выше пределах координаты оптимального плана двойственной задачи, Y*= (,) не меняются, и новое значение целевой функции Z_новое найдем по формуле:

Z_новое =Z*±ΔZ,