Последовательность выполнения расчетов выправки железнодорожной кривой методом Поликарпова

62. Последовательность выполнения расчетов выправки железнодорожной кривой методом Поликарпова.

Среди большого количества методов и приемов расчета рихтовох кривых в данных методических указаниях предпочтение отдано изложен­ному ниже методу инж. Поликарпова, т.к. он, во-первых, является наибо­лее теоретически обоснованным, во-вторых, положен в основу многих других методов расчета.

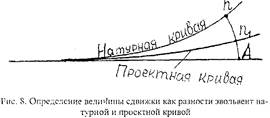
Метод Поликарпова является графоаналитическим, совмещающим аналитическую и графическую части расчета. Он основан на том, что сдвижка каждой точки кривой из некоторого первоначального, натурного, положения в проектное происходит по траектории эвольвенты, или раз­вертки. Поэтому величина сдвижки из сбитого (натурного) положения данной точки кривой в геометрически правильное (проектное) принимает­ся с достаточной точностью как разность эвольвент (рис.8):

где   Ен = An - эвольвента натурной кривой,

        Еп = A_n1 - эвольвента проектной кривой

Поскольку исходным материалом для расчета выправки являются только замеренные стрелы прогиба натурной кривой и стрелы проектной кривой, намечаемые при расчете выправки, величины эвольвент натурной

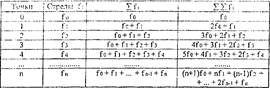
В общем виде длина эвольвенты любой точки кривой определяется как

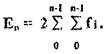
Чтобы найти величины сдвига в заданной точке п , достаточно оп­ределить разность эвольвент натурной и проектной кривых:

где Fi — стрелы прогиба соответствующих точек проектной кривой.

Таким образом, первое положение расчета выправки кривых:

сдвиг в любой точке кривой из натурного в некоторое другое положение, называемое проектным, равен удвоенной сумме сумм разностей натурных и проектных стрел от начета кривой до данной точки (не включая се).

Второе положение: при перемещении одной точки деления кривой на некоторую величину £ стрелы в двух смежных с нею точках изменяют­ся на величину /2 . взятую с обратным знаком.

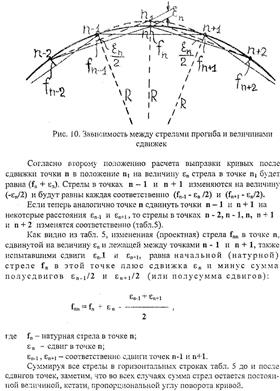
Второе положение целиком вытекает из геометрического построения (рис. 10) и является приближенным, так как изменения стрел в центральной и смежных с нею точках расположены на радиусах одной и той же кривой, которые не могут быть взаимно параллельны, как это предполагается в расчете. Однако погрешность приближения в данном случае настолько ма­ла, что практически ею можно пренебречь.