Несущая способность балласта в зоне рельсового стыка (глава дипломной работы), страница 5

где - среднее квадратическое отклонение динамической нагрузки колеса на

            рельс, Н.

      Уравнение для определения средней динамической нагрузки колеса на рельс имеет следующий вид:

,

где  - статическая нагрузка колеса на рельс, Н;

         - дополнительная сила инерции от колебания кузова на рессорах, Н.

      Определим :

,

где - вертикальная составляющая нагрузки, возникающая за счёт колеба-

              ния кузова на рессорах, Н:

,

              где  - максимальный прогиб рессор при движении, м;

                       - жёсткость   комплекта   рессор,   отнесённая   к   одному

                               колесу, кН/м.

      Максимальный прогиб рессор для четырёхосного вагона определяется по следующей формуле:

,

где  - скорость движения, м/с.

      Среднее квадратическое отклонение динамической нагрузки колеса на рельс  определим по формуле:

,

где - среднее квадратическое отклонение от силы инерции, возникающей

             при колебании кузова на рессорах:

.

     - среднее квадратическое отклонение от силы инерции, возникающей

             при прохождении колесом неровности пути:

,

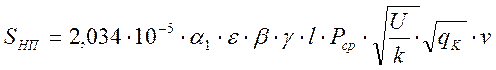             где - коэффициент, учитывающий изменение величины колеблю-

                          щейся массы пути на железобетонных шпалах по сравнению

                          с путём на деревянных шпалах;

                     - коэффициент, учитывающий влияние жёсткости пути на ук-

                          лон динамической неровности;

                    - коэффициент, учитывающий влияние типа рельса на образо-

                          вание динамической неровности на пути;

                     - коэффициент, учитывающий влияние рода балласта на обра-

                          зование динамической неровности на пути;

                     - расстояние между осями шпал;

                   - неподрессоренная масса, отнесённая к одному колесу.

     - среднее квадратическое отклонение от силы инерции, возникающей

               при качении колеса, имеющего изолированную неровность:

,

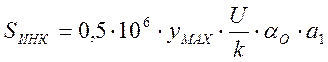               где - максимальный  дополнительный   прогиб  рельса  при  про-

                                хождении  колесом   косинусоидальной  неровности,  отне-

                                сённый  к единице глубины  неровности  (безразмерная ве-

                                личина);

                          - расчётная глубина изолированной неровности на колесе:

,

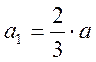                                где  - предельно допустимая глубина ползуна на колёсах.

     - среднее квадратическое отклонение от силы инерции, возникающей

               при качении колеса, имеющего непрерывную неровность:

,

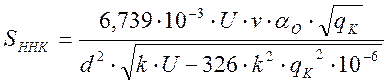               где - диаметр колеса, м.

      Представим основные расчётные характеристики верхнего строения пути и подвижного состава в таблице 6.3.

                                                                                             Таблица 6.3.

Характеристика	Ед. изм.	Величина
1	2	3
Характеристики подвижного состава (четырёхосный вагон).
Статическая нагрузка колеса на рельс.	Н	115000 125000 135000 145000 150000
Расстояние между осями в тележке.	м	1,85
Неподрессоренная масса, отнесённая к одному колесу.	Н	9950
Жёсткость комплекта рессор, отнесён- ная к одному колесу.	Н/м	2000000
Диаметр колеса по кругу катания.	м	0,95

                                                                    Продолжение таблицы 6.3.

1	2	3
Скорость движения.	м/с	25
Расчётная глубина изолированная не- ровность на колесе.	м	0,00067
Характеристики ВСП (прямая):
конструктивные
Тип рельса.	-	Р65
Приведённый износ.	м	0,006
Материал шпал.	-	железобетон
Эпюра шпал.	шт./км	1840
Материал балластного слоя.	-	щебень
Толщина балласта под подошвой шпа- лы.	м	0,4
расчётные
Модуль упругости подрельсового ос- нования.	МПа	150
Коэффициент соотносительной жёст- кости подрельсового основания и рельса.	м-1	1,536
Коэффициент учитывающий измене- ние колеблющейся массы пути на железобетонных шпалах по сравне- нию с путём на деревянных шпалах.	-	0,931
Коэффициент, учитывающий влияние жёсткости пути на уклон динамичес-кой неровности.	-	0,322
Коэффициент, учитывающий влияние типа рельса на образование динами- ческой неровности на пути.	-	0,87
Коэффициент, учитывающий влияние рода балласта на образование динами- ческой неровности на пути	-	1,0
Расстояние между осями шпал.	м	0,55
Площадь полушпалы с учётом изгиба.	м2	0,2975

      Все расчёты по определению максимальная динамическая нагрузка коле- са на рельс  будем вести в табличной форме (таблица 6.4).

Таблица 6.4.

, кН	, кН	, кН	,  кН	, кН	, кН	, кН	, кН	, кН	, кН
115	45,92	34,44	149,44	3,67	10,75	19,38	1,88	12,29	174,42
125	45,92	34,44	159,44	3,67	11,46	19,38	1,88	12,93	185,62
135	45,92	34,44	169,44	3,67	12,18	19,38	1,88	13,57	196,84
145	45,92	34,44	179,44	3,67	12,90	19,38	1,88	14,22	208,07
150	45,92	34,44	184,44	3,67	13,26	19,38	1,88	14,54	213,70

      Расчёты по определению напряжений в балласте сведём в таблицу 6.5.

Таблица 6.5.

, кН		, кН	, кН	, МПа
149,44	-0,0385	174,42	174,42	0,25
159,44	-0,0385	185,62	185,62	0,26
169,44	-0,0385	196,84	196,84	0,28
179,44	-0,0385	208,07	208,07	0,29
184,44	-0,0385	213,70	213,70	0,30