Работа балластных материалов, воспринимающих колебания от проходя- щих поездов, достаточно точно описывается уравнениями движения и урав- нениями предельного напряжённого состояния. Совместное решение этих уравнений в условиях плоской задачи при прочностных характеристиках, зависящих от вибродинамического воздействия, позволит получить предель- ные значения напряжений, которые может воспринимать балласт при усло- вии полного использования прочности материалов, слагающих балластную призму. Система уравнений выглядит следующим образом:
![]()
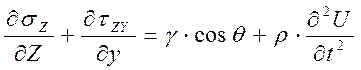
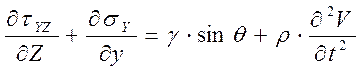
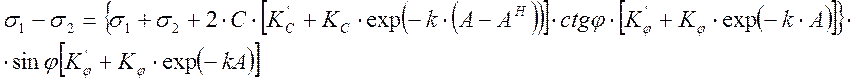
где ![]() и
и![]() – вертикальная и горизонтальная
составляющие нормальных на-
– вертикальная и горизонтальная
составляющие нормальных на-
пряжений;
![]() и
и ![]() – составляющие касательных напряжений;
– составляющие касательных напряжений;
![]() – угол наклона оси Y к горизонту;
– угол наклона оси Y к горизонту;
![]() – масса грунта (
– масса грунта (![]() );
);
![]() – объёмная масса грунта;
– объёмная масса грунта;
![]() – ускорение свободного падения;
– ускорение свободного падения;
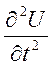 –
действующее ускорение в вертикальной плоскости;
–
действующее ускорение в вертикальной плоскости;
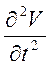 – действующее ускорение в
горизонтальной плоскости;
– действующее ускорение в
горизонтальной плоскости;
![]() и
и
![]() – главные напряжения;
– главные напряжения;
![]() –
коэффициент виброразрушения балласта;
–
коэффициент виброразрушения балласта;
![]() –
амплитуда колебаний балласта в контакте со шпалой, мкм;
–
амплитуда колебаний балласта в контакте со шпалой, мкм;
![]() и
и
![]() – показатели относительного снижения
удельного сцепления и угла
– показатели относительного снижения
удельного сцепления и угла
внутреннего трения под воздействием вибродинамической на-
грузки;
![]() и
и
![]() – показатели отношения минимальных
динамических к статическим
– показатели отношения минимальных
динамических к статическим
характеристикам (соответственно сцепления и угла внутреннего
трения).
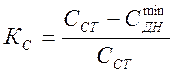 ,
,
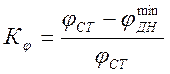 ,
, 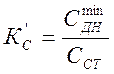 ,
,
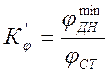 ,
,
где ![]() и
и
![]() – прочностные характеристики при
статической нагрузке;
– прочностные характеристики при
статической нагрузке;
![]() и
и
![]() – минимальные значения удельного сцепления
и угла вну-
– минимальные значения удельного сцепления
и угла вну-
треннего трения, определённые при действии максимальной
вибродинамической нагрузки.
![]()
![]()
Дальнейшие исследование и преобразование основной системы уравне- ний предельного равновесия позволяют получить уравнения характеристик и дифференциальные соотношения вдоль них для случая горизонтального опирания шпалы на балластную призму:
![]()
![]()
Эти два уравнения представляют собой уравнения линий скольжения пер- вого и второго семейства.
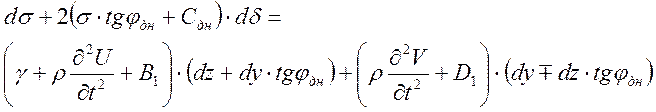
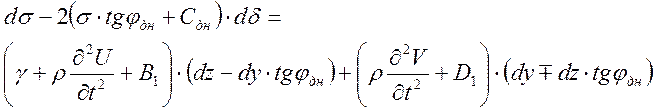
Эти уравнения представляют собой уравнения напряжений и углов.
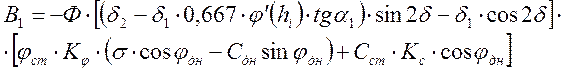
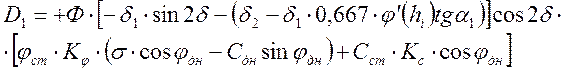
где ![]() -
высота откоса в некоторой точке
-
высота откоса в некоторой точке ![]() ;
;
![]() -
угол наклона наибольшего главного напряжения к оси Y.
-
угол наклона наибольшего главного напряжения к оси Y.
![]()
где ![]() -
угол наклона расчётного откоса к горизонту;
-
угол наклона расчётного откоса к горизонту;
![]() и
и
![]() - коэффициент затухания колебаний в
вертикальной и горизонталь-
- коэффициент затухания колебаний в
вертикальной и горизонталь-
ной плоскостях соответственно.
В рассмотренных уравнениях
неизвестными являются только выражения 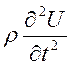 и
и 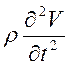 , которые определяются по следующим
формулам:
, которые определяются по следующим
формулам:
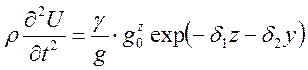
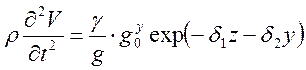
Таким образом, для определения величин предельных напряжений есть все необходимые основные уравнения.
Анализ потенциальных возможностей разрушения балласта показывает, что оно принципиально возможно в двух направлениях: разрушения со смещением материала в направлении откоса балластной призмы (рис. 6.4) и разрушение с выдавливанием балласта в междушпальное пространство (рис. 6.5).
Расчетная схема разрушения со смещением материала в направлении откоса балластной (схема “а”) будет представлена полуплоскостью, ограни-
ченной откосом:
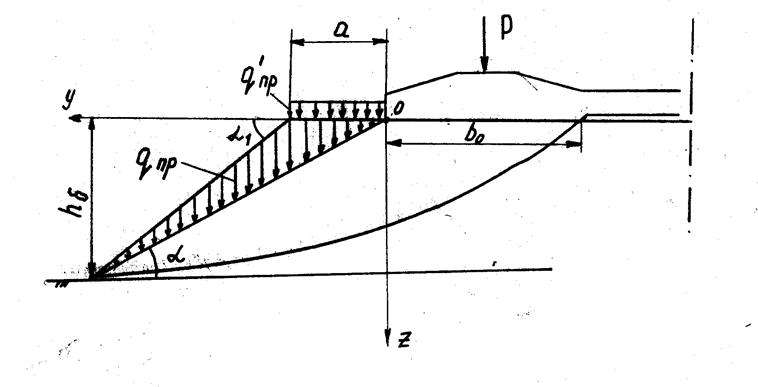
Рис.6.4. Схема разрушения со смещением материала в направлении откоса балластной призмы.
Расчетная схема разрушения с выдавливанием балласта в междушпаль- ное пространство (схема “б”) будет представлена полуплоскостью в сечении по продольной плоскости рельса:
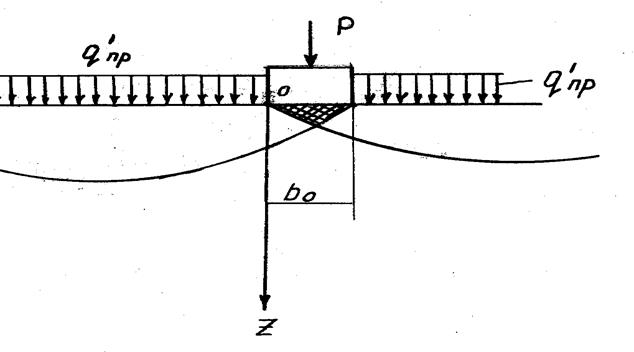
Рис.6.5. Схема разрушения с выдавливанием балласта в междушпальное пространство.
В рассматриваемых схемах имеем:
b0 - размер грузовой площадки для схемы «а» - 0,96м, для схемы «б» - 0,30м;
![]() - вес балласта,
лежащего выше подошвы шпалы принимается 15см, что составит 0,24 т/м2;
- вес балласта,
лежащего выше подошвы шпалы принимается 15см, что составит 0,24 т/м2;
![]() - угол
заложения балластной призмы, при 1:1,5 он равен
- угол
заложения балластной призмы, при 1:1,5 он равен ![]() ;
;
![]() - угол заложения
расчетного откоса;
- угол заложения
расчетного откоса;
а - ширина плеча балластной призмы, м;
hб – толщина балласта, м.
Перед определением несущей способности балластной призмы
определим напряжения в балласте от воздействия подвижного состава. Они
определяют- ся по следующей формуле, ![]() :
:
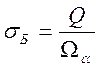 ,
,
где ![]() - нагрузка на шпалу,
- нагрузка на шпалу, ![]() ;
;
![]() - площадь полушпалы с
поправкой на изгиб,
- площадь полушпалы с
поправкой на изгиб, ![]() .
.
Нагрузка на шпалу определяется по следующей формуле:
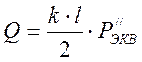 ,
,
где ![]() - коэффициент соотносительной
жёсткости подрельсового основания и
- коэффициент соотносительной
жёсткости подрельсового основания и
рельса, ![]() :
:
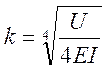 ,
,
где ![]() - модуль упругости
подрельсового основания, МПа;
- модуль упругости
подрельсового основания, МПа;
![]() - модуль упругости
рельсовой стали (
- модуль упругости
рельсовой стали (![]() ), МПа;
), МПа;
![]() - момент инерции
поперечного сечения рельса относительно его
- момент инерции
поперечного сечения рельса относительно его
его центральной горизонтальной оси, проходящей через центр
тяжести сечения, м4.
![]() - расстояние между осями
шпал, м;
- расстояние между осями
шпал, м;
![]() - эквивалентная сила для определения
- эквивалентная сила для определения
![]() , которая оказывает на рельс
, которая оказывает на рельс
такое же воздействие, как и заданная система статических грузов с
учётом динамических составляющих, возникающих при движении.
Эквивалентная сила ![]() определяется по
следующей формуле:
определяется по
следующей формуле:
![]() ,
,
где ![]() - максимальная динамическая
нагрузка колеса на рельс,
- максимальная динамическая
нагрузка колеса на рельс, ![]() ;
;
![]() - средняя динамическая
нагрузка колеса на рельс,
- средняя динамическая
нагрузка колеса на рельс, ![]() ;
;
![]() - сумма воздействий соседних с
расчётным колёсом тележки, ко-
- сумма воздействий соседних с
расчётным колёсом тележки, ко-
торые реализуют средние динамические воздействия, умножен-
ные на значение функции ![]() .
.
![]() - расстояние от
расчётного колеса до
- расстояние от
расчётного колеса до ![]() колеса, м.
колеса, м.
Эквивалентная сила ![]() зависит от вида
подвижного состава, от коли- чества осей в тележке, от расстояния между осями в
тележке.
зависит от вида
подвижного состава, от коли- чества осей в тележке, от расстояния между осями в
тележке.
Для определения эквивалентной силы построим линию влияния.
![]()
![]()
![]()

 l= 1,85м.
l= 1,85м.
![]()
![]()
![]()
![]()
 3π/4k
3π/4k
Рис.6.10. Схема для определения наиболее неблагоприятного
положения нагрузки
Пользуясь схемой рис.6.10 запишем формулу для определения эквива- лентной силы:
![]()
Максимальная динамическая
нагрузка колеса на рельс ![]() определяется по следующей формуле:
определяется по следующей формуле:
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.