Методические указания к лабораторным работам "Градуирование электростатического вольтметра с помощью электрометра Томсона", "Изучение топографии электростатического поля", "Законы разветвлённых цепей постоянного тока", страница 6

2.  Яворский Б.М., Детлаф А.А. Курс физики. – М.: Изд-во «Академия», 2003. – 720 с.

3.  Трофимова Т.И. Курс физики. – М.: Высшая школа, 2004. – 544 с.

4.  Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006. – 30 с.

5.  Физическая энциклопедия (ФЭ). – М.; Научное издательство «Большая Российская энциклопедия». – 1992.

Работа 16

ОПРЕДЕЛЕНИЕ ОМИЧЕСКОГО СОПРОТИВЛЕНИЯ

ПРИ ПОМОЩИ МОСТА УИТСТОНА

Цель работы. Экспериментальное определение сопротивления проводников и проверка закона Ома с помощью моста постоянного тока.

Приборы и принадлежности: потенциометр (или реохорд), магазин сопротивлений, гальванометр, источник э.д.с., неизвестные сопротивления, ключи, провода.

Введение

Физическая сущность сопротивления раскрывается в классической электронной теории металлов Друде. Для объяснения проводимости металлов Друде разработал простой механизм, исходя из представления о том, что металлы являют собой пространственно упорядоченную совокупность атомов (кристаллическую решетку). Электроны внешних оболочек атомов настолько слабо связаны с ядром собственного атома, что образуют совокупность не связанных с отдельными атомами электронов в металле, так называемый «электронный газ». Описание поведения этого электронного газа при изменении внешних условий в первом приближении можно проводить с помощью классической кинетической теории газов. Такие электроны совершают хаотическое тепловое движение и сталкиваются с положительными ионами кристаллической решетки и друг с другом. Ионы же совершают хаотические тепловые колебания около положения своего равновесия.

При наложении внешнего электрического поля напряжённостью  все свободные электроны приобретают определенную скорость упорядоченного движения, направленного против поля. В результате действия двух противоположных факторов (хаотического теплового движения и упорядоченного движения под действием электрического поля – дрейфа) устанавливается стационарный процесс, который характеризуется определенной средней скоростью упорядоченного перемещения свободных электронов. Вдоль поля течет постоянный электрический ток, плотность которого jопределяется законом Ома:

,

где s – удельная электропроводность.

Удельная электропроводность определяется природой материала проводника и внешними условиями, в которых он находится. С этими же факторами связано и число столкновений электронов с ионами решетки, которое тем больше, чем больше длина проводника l и меньше его сечение S. Количественно это обстоятельство отразилось в формуле для сопротивления проводника

R = r,

где r – удельное сопротивление проводника, связанное с удельной электропроводностью соотношением

r = .

Метод измерения и описание аппаратуры

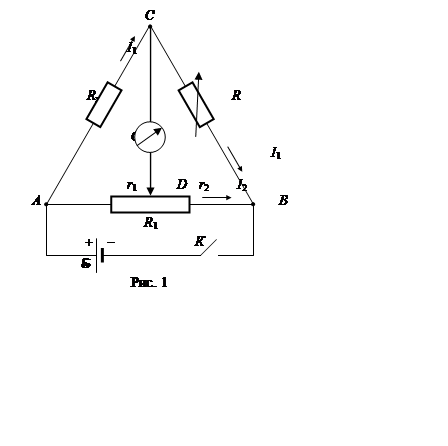
Мостовая схема постоянного тока, часто называемая мостом Уитстона (рис. 1), содержит источник электродвижущей силы E, чувствительный гальванометр G и сопротивления R, R_x, r₁ + r₂ = R₁.

При произвольном соотношении сопротивлений, составляющих всю мостовую схему, через гальванометр при замыкании ключа K должен идти ток.

Однако существует одно определенное соотношение между сопротивлениями, составляющими схему, при котором ток, идущий через гальванометр, обращается в нуль. При этом во всех других звеньях схемы ток не равен нулю.

Для того, чтобы в гальванометре отсутствовал ток, потенциалы в точках С и D должны быть одинаковы:

φ_C = φ_D.

Но это, как видно из схемы, будет иметь место лишь в том случае, если равны друг другу разности потенциалов между точками A и С и точками А и D: а также разности потенциалов между точками С и В и точками D и В:

φ_C – φ_B = φ_D – φ_B.

Ток I, идущий от батареи, разветвляется в точке A на ток I₁, идущий от точки A к точке С, и ток I₂, идущий от А к D. Если в диагонали СD ток отсутствует, то по закону сохранения заряда ток в проводнике АС равен току в проводнике СВ, а ток в проводнике АD равен току в проводнике DВ. Тогда по закону Ома для АС, АD, СВ и DВ можно записать соответственно

I₁R_x =  j_А - j_С;                               I₁R =  j_C - j_B;

I₂r₁ =  j_А - j_D;                               I₂r₂ =  j_D - j_В.

Подстановка полученных величин соответственно в соотношения (1) и (2) дает:

I₁R_x = I₂r₁;                                             (3)

I₁R = I₂r₂.                                              (4)

Разделим уравнение (3) на (4), при этом получим соотношение:

R_x = R(r₁/r₂),                                          (5)

Это соотношение может быть получено также с помощью уравнений Кирхгофа. Равенство (5) может служить для отыскания любого из четырех сопротивлений, включенных в плечи моста, если известны три других сопротивления. Поэтому сущность процесса измерения неизвестного сопротивления на мостовой схеме заключается в экспериментальном подборе величин R, r₁, r₂, при которых ток, текущий через гальванометр, обращается в нуль. Это является необходимым и достаточным условием для расчета неизвестного сопротивления по соотношению (5).

Необходимо помнить, что эта схема применима лишь для сопротивлений, значительных по сравнению с сопротивлением подводящих проводов, ибо только в этом случае можно пренебречь сопротивлением последних.

Мостовая схема реализуется следующим образом. В одно из плеч моста включается известное сопротивление R, например магазин сопротивлений, в другое плечо – неизвестное сопротивление R_х. Наконец, третье и четвертое плечи мостовой схемы составляют сопротивления r₁ и r₂. Они реализуются в виде металлического проводника (реохорда), однородного по химическому составу, с постоянным поперечным сечением. Соединение гальванометра с реохордом осуществляется с помощью подвижного контакта движка D, скользящего по реохорду. Таким образом, сопротивлениями r₁ и r₂ служат отрезки проводника, расположенные по разные стороны от движка D. Такая система скользящего контакта мостика позволяет легко изменять величины сопротивлений r₁ и r₂. Ввиду однородности реохорда отношение сопротивлений r₁ и r₂ можно заменить отношением длин соответствующих отрезков реохорда l₁ и l₂. Тогда соотношение (5) будет иметь вид