Методические указания к лабораторным работам "Градуирование электростатического вольтметра с помощью электрометра Томсона", "Изучение топографии электростатического поля", "Законы разветвлённых цепей постоянного тока", страница 10

 = s,                                             (1)

где s – удельная электропроводность вещества.

Эту формулу называют законом Ома в дифференциальной форме. Рассмотрим этот закон подробнее. Существование напряженности электрического поля указывает на изменение потенциала вдоль проводника. Следовательно, условием существования электрического тока на участке цепи является наличие разности потенциалов на концах этого участка.

Один из источников создания электрического поля внутри проводника – избыточный положительный или отрицательный заряд, накапливающийся в некоторых участках проводника. Но это поле, имеет электростатическое происхождение, одно не может поддерживать в цепи постоянный электрический ток, так как электростатические силы способствуют сближению разноименных зарядов и выравниванию потенциала проводника. Для поддержания постоянного тока в цепи, в ней на некоторых участках должны существовать силы не электростатического происхождения. Эти силы поддерживают такое распределение зарядов в проводниках, которое создает внутри них поле с напряженностью, не равной нулю. При этом на некоторых участках цепи силы не электростатического происхождения заставляют свободные носители зарядов двигаться против поля, вызванного электростатическими силами.

Силы не электростатического происхождения называют сторонними. Они могут быть обусловлены химическими про­цессами, диффузией носителей зарядов в неоднородной среде или через границу двух разнородных веществ, явлением элек­тромагнитной индукции и т. д. С учетом всех сил, действующих на заряды, формулу (1) записывают в более общем виде:

 = s( + ),                                     (2)

Иными словами, в уравнении (1)

 =  + ,

и здесь – напряженность поля сторонних сил, то есть сил не электростатического происхождения, действующих на пробный единичный положительный заряд, – напряженность поля кулоновских сил.

Сторонние силы в практике удобно характеризовать не напряженностью, а работой, которую они совершают при переносе единичного положительного заряда. Эта работа называется электродвижущей силой (э.д.с.), обозначается буквой E и может быть выражена в виде интеграла, пределы которого обозначены соответственно 1 и 2:

E=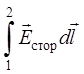,                                            (3)

где dl–элемент проводника с током.

На основании равенства (2) запишем интеграл для участка 1 – 2:

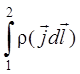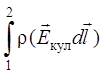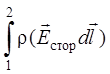 =  + ,                        (4)

где r =  – удельное сопротивление проводника.

Предположим, что ток течет по прямолинейному однородному проводнику и на участке 1 – 2 постоянен. Вынесем r за знак интегралов в правой части уравнения и разделим на r обе части уравнения. В правой части полученного равенства первое слагаемое есть разность потенциалов на концах участка 1 – 2:

j₁ - j₂ = r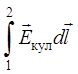,                                      (5)

а второе – э.д.с. на этом участке:

E_2-1 =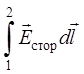,                                           (6)

Подставим уравнения (5) и (6) в уравнение (4) и учтем, что вектор  совпадает по направлению с . С учётом того, что поперечное сечение проводника  перпендикулярно этим векторам, уравнение (4) примет вид:

r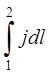 = j₁ - j₂ + E_2-1,                                  (7)

где

j = ,                                             (8)

а I– сила постоянного тока. В результате получим:

I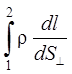 = j₁ - j₂ + E_2-1,                                  (9)

С учётом того, что 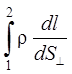 – электрическое сопротивление участка 1 – 2, формула (9) принимает вид:

IR_1-2 = j₁ - j₂ + E_2-1.                                   (10)

Полученное уравнение носит название закона Ома для участка цепи, содержащего э.д.с.

Иногда его записывают в виде:

I = 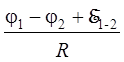                                        (11)

и называют обобщенным законом Ома.

При записи этого уравнения применяется правило знаков, согласно которому, если направление токов совпадает с направлением обхода участка цепи 1 – 2, то ток в уравнении (11) считается положительным. Если в направлении обхода участка от точки 1 к точке 2 потенциал источника E_2-1 повышается, то э.д.с. берется с плюсом, в противном случае с минусом.

Описание эксперимента

В лабораторной работе используется электрическая цепь, состоящая из трех ветвей, в каждую из которых включен источник тока, сопротивление, микроамперметр, двухпозиционный двухполюсный переключатель (рис. 2).

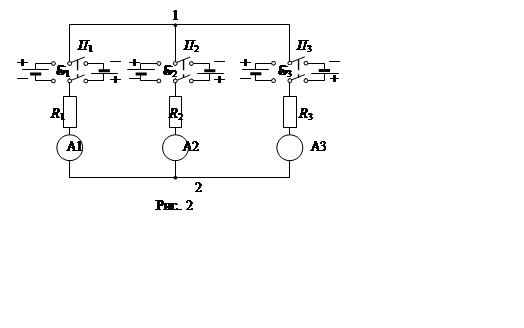Источники тока включаются в цепь с помощью переключателей П₁, П₂, П₃, которые позволяют менять направление сторонних сил и, соответственно, знак э.д.с. в ветви. Знак э.д.с. определяется правилом, приведённым во введении к данной лабораторной работе.

Пусть выбранным направлением считается направление от узла 1 к узлу 2, тогда, если в этом направлении потенциал источника э.д.с. возрастает, то E > 0. В противном случае, наоборот,E < 0.

Для каждой из трех ветвей запишем обобщенный закон Ома. Так, например, для ветви 1:   I₁ = 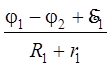, где R₁ – сопротивление, r₁ – общее сопротивление источника э.д.с. E₁ и амперметра A₁. В написанном равенстве и во всех последующих будем считать E₁, E₂, E₃ алгебраическими значениями э.д.с.

Из уравнения (11) получаем:

j₁ - j₂ = I₁(R₁ + r₁) - E₁.                               (12)

Так как все ветви в схеме параллельны друг другу, то разность потенциалов на всех ветвях равна j₁ - j₂.  Величины токов в них равны, соответственно,

I₂ = 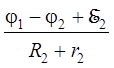,     I₃ = 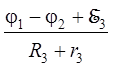,                    (13)

где r₂ и r₃ – значения внутреннего сопротивления источников тока и амперметров в ветвях 2 и 3. Из выражения (10) получим:

E₂ = I₂(R₂ + r₂) - (j₁ - j₂),     E₃ = I₃(R₃ + r₃) - (j₁ - j₂).      (14)

Пусть E₁ и все значения сопротивлений известны, тогда, измерив значения силы тока в ветвях, по уравнению (12) можно рассчитать разность потенциалов j₁ - j₂, а затем по формулам (14) – значения E₂ и E₃.

Порядок выполнения работы

1. Проверить и отрегулировать при необходимости нулевое положение стрелок микроамперметров, после чего шнур питания схемы включить в сеть.