Так как электрические силы являются центральными, работа силы, действующей на точечный заряд q0 в электрическом поле при его перемещении, не зависит от формы траектории, а зависит лишь от начального и конечного положения заряда. Такие поля называются потенциальными и работа по перемещению заряда q0 из точки 1 в точку 2 может быть представлена как разность значений потенциальных энергий WП, которыми обладал заряд q0 в точках 1 и 2:
A12 = WП1 − WП2 (2)
Потенциальная энергия пропорциональна величине заряда q0, перемещаемого в данном поле, а отношение потенциальной энергии к величине заряда не зависит от величины q0 и поэтому характеризует само электрическое поле.
Потенциалом j данной точки электростатического поля называется скалярная величина, равная отношению потенциальной энергии WП, которой обладает положительный пробный точечный электрический заряд q0, помещенный в данную точку поля, к величине этого заряда:
j =
. (3)
Разность потенциалов между точками 1 и 2 электрического поля определяется из выражения (2):
j1 - j2 =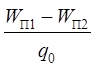 
= 
,
(4)
т. е. разность потенциалов равна отношению работы по перемещению заряда q0 из точки 1 в точку 2 к величине этого заряда.
Как и потенциальная энергия, потенциал электрического поля зависит от выбора точки, в которой потенциал считается равным нулю. Такой точкой условились считать точку, удаленную от заряда на бесконечность. Тогда j2 = 0, и
j1 = 
.
(5)
Следовательно, потенциал данной точки поля равен отношению работы, совершенной силами электрического поля по переносу пробного точечного заряда q0 из данной точки поля в бесконечность (или в точку поля, для которой потенциал условно принято считать равным нулю), к величине переносимого заряда.
Потенциал – скалярная величина, положительная или отрицательная, в зависимости от знака работы (пробный заряд q0 условились всегда брать положительным). Из выражения (5) следует, что потенциалы всех точек вокруг положительного заряда положительны, вокруг отрицательного – отрицательны.
Потенциал является энергетической характеристикой электрического поля.
Единицей потенциала в СИ является 1 В = 1 Дж/Кл.
Для графического изображения электростатического поля кроме силовых линий используют эквипотенциальные поверхности.
Эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Уравнение эквипотенциальной поверхности имеет вид
j(x, y, z) = const.
Эквипотенциальные поверхности условились проводить таким образом, чтобы разность потенциалов для двух соседних поверхностей была всюду одна и та же. На плоском рисунке изображают эквипотенциали – линии пересечения эквипотенциальных поверхностей с плоскостью чертежа.
Напряженность
электрического поля 
и потенциал j связаны между собой. Действительно, в потенциальном
поле консервативных сил взаимосвязь силы 
и
потенциальной энергии WП имеет вид:
= - gradWП.
(6)
Разделив обе части равенства (6) на q0, получаем:
= - gradj,
(7)
где gradj − вектор, который называется «градиент
потенциала j». Знак минус
указывает на то, что вектор направлен в
сторону убывания потенциала. Градиент функции j(х, у, z) в декартовой системе координат имеет
вид:
gradj =
+ 
+ 
,
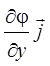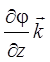где 
, 
, 
−
единичные векторы, т. е. орты соответствующих координатных осей; 
, 
, 
− частные производные потенциала.
Для
произвольного направления работа сил электростатического поля на малом
перемещении 
пробного заряда q
dA = q = qEdlcos(^) = qEℓdl, (8)
где Eℓ − проекция вектора на направление перемещения . С другой стороны
dA = −dWП = −qdj. (9)
Из соотношений (8) и (9) следует, что
Eℓ = -
,
(10)
т.е. проекция вектора напряженности электростатического поля на произвольное направление равна быстроте убывания потенциала в этом направлении.
При перемещении
по эквипотенциальной поверхности на отрезок dl потенциал не изменяется (dj = 0). Следовательно, согласно (10), касательная к поверхности
составляющая вектора равна нулю.
Отсюда вытекает, что силовые линии вектора напряженности электростатического
поля в каждой точке ортогональны к эквипотенциальным поверхностям.
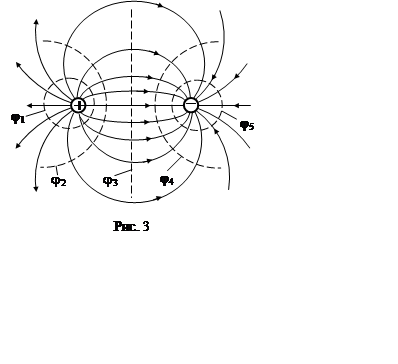
Из условия ортогональности силовых линий и эквипотенциальных поверхностей следует, что для графического описания поля достаточно каким-либо образом определить положение только эквипотенциальных поверхностей и затем, пользуясь этим условием, построить силовые линии. В качестве примера на рис. 3 представлены эквипотенциали (пунктирные) и силовые линии (сплошные) для поля двух точечных зарядов. При одновременном использовании эквипотенциалей и силовых линий картина поля становится более наглядной.
Можно математически решить задачу о
распределении в пространстве вектора напряженности и
потенциала φ, найдя аналитические зависимости и
j как функции координат x, y, z. Однако математический расчет
электрического поля, создаваемого несколькими заряженными телами сложной
конфигурации, иногда трудно осуществить. В таких случаях, моделируя реальные
условия, находят распределение электрического поля опытным путем. При этом
следует помнить, что графическое изображение в таких случаях часто является
плоским, так как проводятся только те силовые линии, которые лежат в плоскости
чертежа.
Из выше изложенного следует, что если известно распределение эквипотенциальных поверхностей в данном поле, то можно получить его изображение с помощью силовых линий и наоборот. Следовательно, можно получить наглядную картину распределения электрического поля, т.е. топографию электрического поля. В данной работе требуется опытным путем выявить расположение эквипотенциалей для заданного вида электродов и затем построить эти линии вместе с силовыми линиями поля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.