Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека: Методические указания к лабораторной работе, страница 3

Записав выражение (13) для каждого элемента массы тела:

- - - - - - -

- - - - - - -

и просуммировав левые и правые части этих равенств с учётом того, что векторы  имеют одинаковые направления и их сумм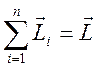а , а 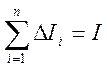 есть момент инерции тела относительно оси вращения, получим:

                            (14)

Однако, между полученным соотношением и соотношением (13) имеется и существенное различие: соотношение (14) справедливо только для однородного тела (т. е. тела с равномерным распределением массы по объёму), вращающегося вокруг своей оси симметрии.

В самом общем случае тел произвольной формы и с произвольным распределением массы по объёму направление векторов  и  не совпадают.

Зависимость (13) сохраняется только для проекций векторов  и  на координатные оси.

 

      ,

где  и  есть главные моменты инерции тела.

При действии на тело внешней силы  согласно основному закону динамики поступательного движения  = d/dtимпульс тела , а следовательно и момент импульса  изменяются. Умножив левую и правую части это выражения на радиус вектор  точки приложения силы, получим:

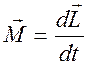                       (15)

(где  момент внешней силы, действующей на тело,  - скорость изменения момента импульса).

Как видно из (15) изменение момента импульса тела  равно импульсу момента приложенной к нему силы . Это более общая формулировка основного закона динамики вращательного движения. Такая формулировка основного закона динамики вращательного движения позволяет применять его и в тех случаях, когда при вращательном движении тела происходит изменение момента инерции тела за счёт перераспределения массы тела относительно оси вращения (например, при работе сепараторов, центрифуг, когда более тяжёлые фракции веществ, загруженных в эти аппараты, под действием центробежных сил смещаются на периферию).

При вращательном движении системы тел, между которыми действуют силы внутреннего взаимодействия  в соответствии с основным законом динамики (15) имеем:

 (*).

Изменение момента импульса системы равно сумме импульсов моментов всех действующих в ней сил.

Для изолированной (замкнутой) системы или системы, на которую действуют внешние силы с уравновешенными моментами . Внутренние силы взаимодействия  в соответствии с третьим законом Ньютона всегда уравновешенны и для них .

Таким образом изменения момента импульса замкнутой системы не происходит (d=0), т.е. момент импульса замкнутой системы есть величина постоянная ().

В процессе движения замкнутой системы моменты импульсов отдельных тел  могут изменяться, но так, что их векторная сумма остаётся неизменной.

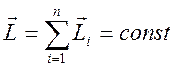                (16)

В этом состоит закон сохранения момента импульса, который вместе с законами сохранения импульса и сохранения механической энергии составляют основное содержание физических основ механики.

Постановка задачи.

Для измерения осевого момента инерции, в работе  используется крестообразный маховик Обербека.

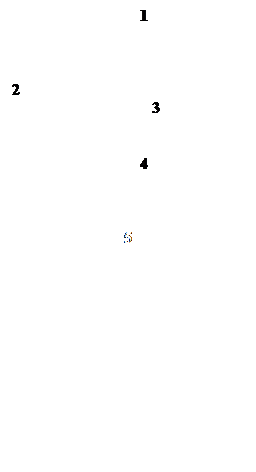Маховик Обербека (рис. 3) представляет собой свободно вращающуюся относительно неподвижной горизонтальной оси крестовину, выполненную в виде четырёх взаимно перпендикулярных металлических стержней. Ось крестовины закреплена на вертикальной стойке, установленной на массивном основании. На стержни одеты цилиндрические муфты (2) известной массы, которые закрепляются на заданном расстоянии r от оси вращения с помощью стопорных винтов.

 Перемещая муфты вдоль стержней на     то    или    иное    расстояние    r,

можно             изменять             осевой

момент инерции системы. Используя зависимость (5), считая что масса однородного цилиндра сосредоточена в его геометрическом центре, где размещён стопорный винт, выразим осевой момент инерции муфт по формуле

                                                                   (17).

На оси маховика жёстко укреплены два соосных шкива различных диаметров d₁ и d₂, на которые в один ряд наматывается нить (нить считаем нерастяжимой и невесомой). Один конец нити прикрепляется к шкиву, к другому концу нити, переброшенной через вспомогательный блок 1, подвешивается груз массой m (4).

Изменением массы груза m, путём наложения перегрузков с массой m₁, можно изменять силу натяжения нити Т, под действием которой маховик совершает равномерно-ускоренное вращательное движение с угловым ускорением , которое согласно основному закону динамики вращательного движения (6) прямо пропорционально моменту силы натяжения нити . Поскольку сила натяжения направлена вертикально, её плечо в соответствии с (3) равно  или .

Одновременно под действием силы тяжести груз m совершает равноускоренное поступательное движение вниз. При этом считаем, что момент сил трения относительно оси вращения маховика мал по сравнению с моментом силы натяжения нити.

На вертикальной стойке прибора укреплены два кронштейна: нижний (5) – неподвижный, верхний (3) – подвижный. Верхний кронштейн можно перемещать вдоль стойки и фиксировать  в любом положении, задавая тем самым длину пути h вертикального перемещения груза m.

Для измерения длины пути на стойке нанесена миллиметровая шкала.

Прибор снабжён счётчиком времени – миллисекундомером, не ведущим отсчёт времени при нажатых кнопках  «сеть» или «сброс».

Измерения времени движения груза m осуществляется с использованием двух фотоэлектрических датчиков, вмонтированных в верхний и нижний кронштейны и подключенных к секундомеру. Расстояние между световыми лучами обоих датчиков равно длине пути вертикального перемещения груза h. Датчики включаются в работу при нажатии клавиши «сеть».

Нажатие клавиши «пуск» включает секундомер и одновременно выключает электромагнит, удерживающий крестовину, после чего начинается вращение крестовины и движение груза m вниз.