Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека: Методические указания к лабораторной работе, страница 2

Через центр инерции тела всегда можно провести три взаимно перпендикулярные оси. Они называются главными осями инерции. У тела с осевой симметрией (цилиндр) одной из главных осей инерции является ось симметрии, в качестве двух других осей могут быть две любые взаимно перпендикулярные оси, лежащие в плоскости, перпендикулярной к оси симметрии, и проходящие через центр инерции тела. У однородного тела с центральной симметрией (шар) главными осями инерции являются три любые взаимно перпендикулярные оси, проходящие через центр инерции.

Моменты инерции относительно главных осей называются главными моментами инерции тела. В общем случае эти моменты инерции различны: . Для тела с осевой симметрией , для тела с центральной симметрией .

Как отмечалось выше, по своему содержанию основной закон динамики вращательного движения (6) аналогичен второму закону Ньютона при поступательном движении, а момент инерции тела при вращательном движении I аналогичен массе тела m при поступательном движении. Однако есть и существенное отличие, состоящее в том, что если масса тела сказывается всегда одинаково, вне зависимости от направления, т.е. является скаляром, то момент инерции тела, зависящий от распределения массы по объёму тела зависит от направления оси вращения, даже если она проходит через центр инерции. Таким образом, для твёрдого тела не удаётся ввести единственного определения момента инерции, но оказывается, что любой момент инерции твёрдого тела может быть представлен в виде совокупности девяти величин, называемых компонентами тензора инерции тела относительно точки, положение которой задано радиус-вектором . Таким образом, если для характеристики массы тела достаточно одной величины (m – скаляр), а для полного определения взаимосвязи трёх векторных величин () достаточно знать три проекции этих векторов на координатные оси, то для полного определения  момента инерции необходимо уже девять величин. Говорят, совокупность девяти величин, имеющих физический смысл моментов инерции тела относительно некоторых осей, проходящих в теле через центр инерции, определяют тензор инерции. Но в силу симметричности тензора инерции достаточно знать только шесть компонентов. Однако для всех твёрдых тел существует три взаимно перпендикулярные оси, для которых только три компонента тензора инерции оказываются отличными от нуля. Эти оси тензора инерции являются также главными осями инерции самого тела.

Как отмечалось выше, для тел правильной формы направление осей тела можно определить, пользуюсь соображениями симметрии. Так, для однородного прямоугольного параллелепипеда главные оси параллельны его рёбрам. Для цилиндра одной из главных осей является его ось симметрии. Две любые оси, перпендикулярные оси симметрии и друг другу так же являются  главными осями. Для шара три любые взаимноперпендикулярные оси являются главными.

Если для тела известны главные оси, то можно связать с ними прямоугольную систему координат и поместить её начало в центр инерции. Для каждой оси можно (экспериментально или расчётным путём) найти главные моменты инерции -  соответсвенно. В этом случае момент инерции тела  относительно произвольной оси, не совпадающей ни с одной координатной осью, выражается через главные моменты инерции:

                           (10)

(где  - направляющие косинусы осей вращения).

Формула (10) допускает наглядную геометрическую интерпретацию. Через начало координат О следует провести прямые (оси вращения) во всевозможных направлениях и на них отложить отрезки длиной 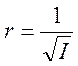. Геометрическим местом концов таких отрезков будет поверхность второго порядка – эллипсоид, называемый эллипсоидом инерции тела относительно точки О, являющейся его центром. Если точка О совпадает с центром инерции тела, то соответствующий эллипсоид называется центральным.

Для динамики вращательного движения твёрдого тела существенна симметрия не самого тела, а симметрия соответствующего ему эллипсоида инерции. Все тела с одинаковыми эллипсоидами инерции динамически эквивалентны. Чтобы эллипсоид обладал симметрией вращения, не обязательно, чтобы само тело обладало той же симметрией. Так, например, если взять однородный параллелепипед с квадратными основаниями и поместить точку на геометрической оси параллелепипеда, то в этом случае эллипсоид инерции будет эллипсоидом вращения, ось симметрии которого совпадает с геометрической осью параллелепипеда. В динамическом отношении движение такого параллелепипеда, описывается такими же уравнениями, что и движение однородного цилиндра. Если параллелепипед вырождается в куб, а начало координат помещено в его центре, то эллипсоид инерции вырождается в сферу. В динамическом отношении однородный куб ведёт себя так же, как однородный шар.

Основной закон динамики вращательного движения можно записать в более общей форме, учитывающей возможное перераспределение массы тела относительно оси вращения или относительно центра инерции в процессе его движения. Для этого вводится понятие момента импульса .

Моментом импульса i-го элемента тела называется векторное произведение:

              (11).

Соответственно моментом импульса материальной точки с массой m движущейся со скоростью по окружности радиуса  является векторное произведение:

                   (12).

Вектор , в соответствии с правилами умножения векторов  и , лежащих в плоскостях вращения, перпендикулярен этой плоскости, и направлен в ту же сторону что и вектор угловой скорости . В этом легко можно убедиться подстановкой в (12) линейной скорости , выраженной через угловую скорость вращения  =  ^.

Согласно (5) произведение  есть момент инерции материальной точки . Следовательно

                  (13).

Размерность момента импульса [L] = .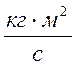

Таким же соотношением устанавливается связь между моментом импульса и угловой скоростью тела конечных размеров.