Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека: Методические указания к лабораторной работе

УДК  531

М - 38   

Марченко В.И. Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека. Методические указания к лабораторной работе.  – М.: МИИТ, 2006,– 20 с.

       Изложены физические основы динамики вращательного движения. Описана методика экспериментального измерения осевых моментов инерции твердых тел на маховике Обербека. Соответствует программе дисциплины «Физика» (раздел «Физические основы механики»). Предназначено для студентов 1 курса энергетических, механических и строительных специальностей.

  Ó Московский государственный                                                                 университет путей сообщения

                                                             ( МИИТ), 2006

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Физика-I»

В. И. Марченко

                                    Утверждено

                                              редакционно-издательским

                                      советом университета

ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ И ИЗМЕРЕНИЕ ОСЕВЫХ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ НА МАХОВИКЕ ОБЕРБЕКА.

Методические указания к лабораторной работе по дисциплине «Физика» №104 для студентов 1 курса энергетических, механических и строительных специальностей.

Москва – 2006

Работа №104. Изучение динамики вращательного движения и измерение осевых моментов инерции твердых тел на маховике Обербека.

Цель работы. Усвоить основной закон динамики вращательного движения. Косвенно измерить момент инерции цилиндрических тел. Установить зависимость осевых моментов инерции вращающихся на маховике грузов от расстояния до оси вращения.

Приборы и принадлежности.Маховик Обербека, автоматический счётчик времени, четыре цилиндрических тела с одинаковой массой, масштабная линейка.

Введение.

Вращательным движением тела назывется такое движение, при котором все точки тела движутся по окружностям, плоскости которых параллельны друг другу, а центры лежат на одной прямой, называемой осью вращения. Для любого элемента массы тела Dm_i, расположенного на расстоянии r_i от оси вращения, существует полная аналогия между законами динамики поступательного и вращательного движений. Умножая левую и правую части основного закона динамики поступательного движения точки a_i = /Dm_i на радиус-вектор точки и, считая что в этой точке сосредоточена часть массы тела , получим: 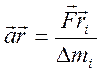 , где a_i – линейное ускорение поступательного движения точки, – сила, приложенная в точке. Заменив в левой части полученнного равенства a_i на угловое ускорение  (связанные соотношением = br_i): 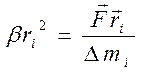, придем к формуле связи между угловым ускорением (одинаковым для любой точки тела) и приложенной силой F_i.

  (*)

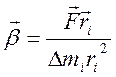В этой формуле векторное произведение  называется моментом силы , действующей на i-ый элемент массы тела, положение которого задано радиусом вектором . В общем виде, когда сила F приложена к телу в точке на растоянии r от оси вращения:

                                               (1)

Как видно из равенства (1), момент силы – это векторное произведение действующей на тело силы на радиус-вектор точки ее приложения.

Векторы  и  лежат в плоскости окружности, по которой движется точка и в соответствии с правилом умножения векторов, лежащих в одной плоскости, вектор-произведение  лежит в перпендикулярной плоскости. Он направлен вдоль оси вращения в ту же сторону, что и вектор угловой скорости . Модуль вектора момента силы вычисляется по формуле:

                                            (2)

(где  - угол между направлением вектора  и направлением действия силы ) (Рис. 1).

Перпендикуляр , опущенный из центра вращения О, на направление действия силы , называется плечом силы. Как видно из рис. 1:

                                           (3)

Заменяя в (2)  на , получим:

                 (4).

Согласно (4) модуль момента силы равняется произведению силы на плечо. Размерность момента силы:

[M] = кг ^. м²/с².

Произведение ² в знаменателе  правой части формулы (*) называется моментом инерции i-го элемента массы тела

                                        ⁽⁵⁾

Момент инерции  характеризует инертные свойства точки тела, в которой сосредоточена малая часть его массы Dm_i, а момент инерции всего тела равен сумме моментов инерции всех точек:

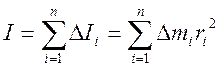            (5’)

Равномерность [I]= кг ^. м².

После подстановки в равенство (*) значений момента силы, действующей на i-ый элемент массы  (1) и момента инерции этого элемента (5) получим: 

                    

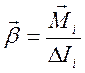
Такое же соотношение сохранится и для всего тела, поскольку угловое ускорение всех его точек одинаково, а отношение 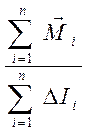 равно отношению момента силы приложенной к телу М к моменту инерции тела относительно оси его вращения I.

Таким образом, мы получили зависимость между угловым ускорением , моментом силы, приложенной к телу М и моментом инерции тела относительно оси вращения I.

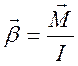                                                                          (6)

Это соотношение является основным законом динамики вращательного движения твёрдого тела, вокруг неподвижной оси, который формулируется так: угловое ускорение тела пропорционально моменту приложенной к телу силы и обратно пропорционально моменту инерции тела относительно заданной оси вращения. 

Он аналогичен второму закону Ньютона при поступательном движении тела с постоянной массой m.

Момент инерции тела относительно оси (осевой момент инерции) в равенстве (6) является аналогом массы, но он зависит не только от величины массы тела, но и от распределения  массы относительно этой оси. Как масса является мерой инертности тела при поступательном движении, так и момент инерции есть мера инертности тела при вращательном движении. Каждое тело, независимо от того, вращается оно или покоится, обладает определённым моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или покоится.

При непрерывном распределении массы тела по его объему вычисление момента инерции сводится к интегрированию бесконечно малых элементов массы dm = r dV, умноженных на квадрат расстояния от оси вращения.

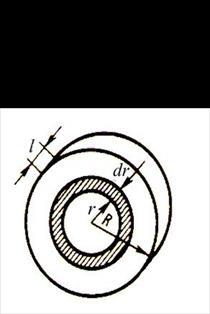
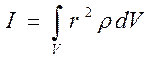              (7)

(где - плотность вещества в элементе объёма тела dV, находящегося на расстоянии r от оси вращения).

Рис.2

Пределы интегрирования в (7) устанавливаются в зависимости от геометрической формы тела. Например, при вращении цилиндра радиусом R относительно оси, проходящей через его центр (рис. 2), элемент объёма dV  выбирается   в    виде    тонкого   цилиндри-

                          ческого слоя радиусом r и толщиной dr.

,

(где l  – длина цилиндра).

Подстановка dV в (7) и интегрирование по переменной r, в пределах от 0 до R даёт:

.

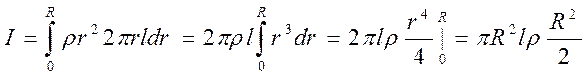Нетрудно увидеть, что - это объём цилиндра V, а =m – его масса. Таким образом, момент инерции цилиндра относительно оси, проходящей через центры его оснований вычисляется по формуле

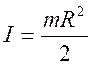            (8).

По формуле (8) вычисляют осевые моменты инерции дисков, блоков, маховых колёс, вращающихся вокруг неподвижной оси, проходящей через центры инерции этих тел, перпендикулярно плоскостям окружностей, по которым движутся точки тела. Центром инерции тела называется точка тела, положение которой относительно начала координат задаётся радиус-вектором  ,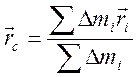

(где m_i – масса i-го элемента тела, а  - радиус-вектор элемента).

Таким же образом можно показать, что момент инерции тонкостенного кольца, обруча или трубы с радиусом R и массой m вычисляются по одинаковой формуле:

          (9).