1. Энергетический и кинематический расчет привода.
1.1. Исходные данные.
![]() – окружное усилие на барабане;
– окружное усилие на барабане;
V = 0,85 м/с – скорость движения ленты;
Dб = 225 мм – диаметр барабана.
1.2. Выбор электродвигателя.
1.2.1. Определение потребляемой мощности привода.
Потребляемую мощность привода (мощность на выходе) для ленточного конвейера определяют по формуле
![]()
1.2.2. Определение потребляемой мощности электродвигателя.
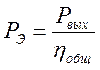 ,
,
где ![]() – общий КПД привода, определяемы как
произведение КПД: 2 муфт
– общий КПД привода, определяемы как
произведение КПД: 2 муфт ![]() , зубчатой
конической передачи
, зубчатой
конической передачи ![]() , зубчатой цилиндрической передачи
, зубчатой цилиндрической передачи
![]() и 3 пар подшипников качения
и 3 пар подшипников качения ![]() .
.
![]() ,
,
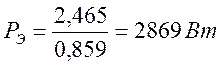
это значение
округляем до ближайшего большего стандартного, т.е. ![]()
1.2.3. Определение предполагаемой частоты вращения вала электродвигателя.
Определяем произведением
оптимального значения передаточных чисел конической ![]() и
цилиндрической
и
цилиндрической ![]() зубчатых передач привода и
заданной частоте вращения приводного вала конвейера
зубчатых передач привода и
заданной частоте вращения приводного вала конвейера ![]()
![]()
Частоте вращения приводного вала ленточного конвейера определяется по формуле
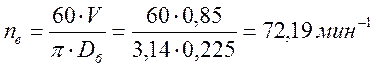
![]()
По требуемым
мощности ![]() и частоте вращения
и частоте вращения ![]() я выбрал электродвигатель АИР112МА6
я выбрал электродвигатель АИР112МА6
Номинальная
частота вращения вала ![]()
1.3. Определение общего передаточного отношения привода и разбивка его по ступеням.
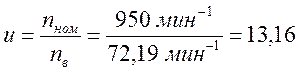 , где u
– общее передаточное число.
, где u
– общее передаточное число.
Рекомендуемые значения передаточных чисел для тихоходной ступени
![]()
Рекомендуемые значения передаточных чисел для быстроходной ступени
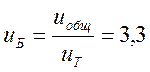
Полученные
передаточные числа отдельных ступеней редуктора привожу к стандартным значениям
по СТ СЭВ 227-75: ![]() ,
, ![]() .
.
1.4. Определение кинематических и силовых характеристик на валах привода.
1.4.1 Определение частоты вращения валов.
Частота вращения I и II валов равны номинальной частоте вращения электродвигателя, так как между ними нет передач, т.е.
![]()
Частота вращения III вала равна отношению частоты вращения II к передаточному числу быстроходной передачи
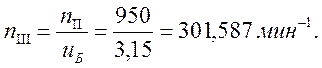
Частота вращения IV вала равна отношению частоты вращения III к передаточному числу тихоходной передачи
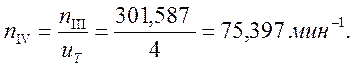
Частота вращения вала барабана равна частоте вращения IV вала.
1.4.2. Определяем угловые скорости валов.
Угловые скорости определяться по формуле
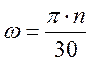 .
.
Угловая скорость I и II валов
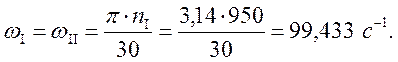
Угловая скорость III вала
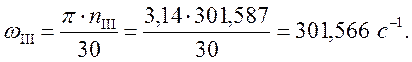
Угловая скорость IV вала и вала барабана
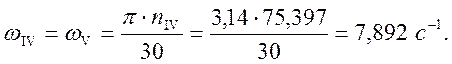
1.4.3. Определяем крутящие моменты на валах.
Для определения крутящего момента на I валу будем использовать формулу
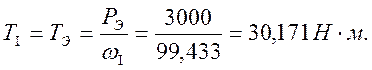
Крутящие моменты на остальных валах определяются произведением крутящего момента на предыдущем валу, передаточного числа между ними и КПД передач, муфт и подшипников на валах.
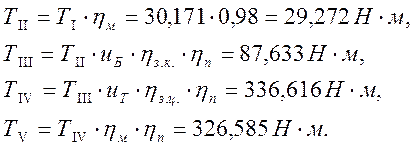
1.4.4. Определяем мощность на валах.
Для определения мощности на валах будем использовать формулу
![]()
Соответственно для каждого вала мощность равна:
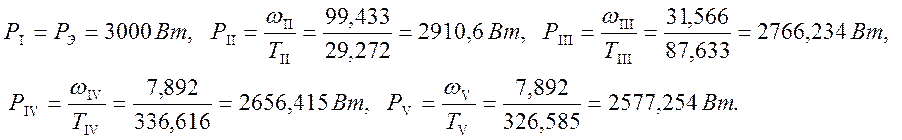
Все значения занесём в таблицу1.1.
Таблица 2.1. Кинематические данные редуктора
3. Расчет зубчатой передачи
3.1.Выбираем сталь 40Х для колеса и шестерни.
Термическая обработка – улучшение. НВ=235÷262, НВср=0,5(235 ÷262)=248,5 – это для колеса. Для шестерни – улучшение и закалка ТВЧ. HRC - 45÷50. HRCср=0,5(45÷50)=47,5 ([1], с.9).
3.2. Допускаемые напряжения.
Определяю
допускаемые контактные напряжения и напряжения изгиба отдельно для колеса [s]Н2
и [s]F2 и шестерни [s]Н1 и [s]F1 по формулам ![]() В
этой формуле
В
этой формуле 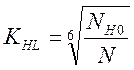 - коэффициент долговечности
при расчёте по контактным напряже-ниям;
- коэффициент долговечности
при расчёте по контактным напряже-ниям; 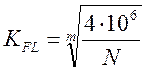 -
коэффициент долговечности при расчёте по изгибу.
-
коэффициент долговечности при расчёте по изгибу.
Находим
действительное число циклов перемены напряжений для колеса ![]() , где
, где ![]() -
время работы передачи.
-
время работы передачи. ![]() , к=0,5 –
для конвейера.
, к=0,5 –
для конвейера.
![]() .
.![]() циклов.
циклов.
Для шестерни ![]() циклов.
циклов.
NH0 – число циклов перемены напряжений, соответствующее пределу выносливости ([3], табл. 3.3., с.51)
NH02 =16,5 млн циклов;
Определяем коэффициенты долговечности
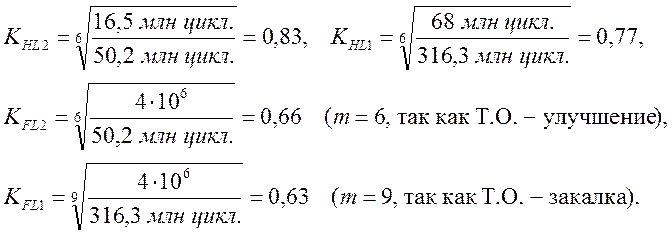
Допускаемые напряжения, соответствующие числу циклов перемены напряжений, ([1], табл. 2.2., с.12).
для колеса ![]()
для шестерни ![]() (пологая, что
модуль m<3);
(пологая, что
модуль m<3);
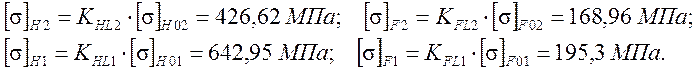
Так как имеем
зубчатую передачу (прямозубую, цилиндрическую), то вместо ![]() в рас-четную формулу подставляем
наименьшее из
в рас-четную формулу подставляем
наименьшее из ![]() и
и ![]() ,
то есть
,
то есть ![]() .
.
3.3. Межосевое расстояние
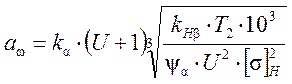 , где
, где ![]() -
вспомогательный коэффициент; для прямозубых колёс
-
вспомогательный коэффициент; для прямозубых колёс ![]() =49,5;
=49,5;
![]() - коэффициент неравномерности нагрузки
по длине зуба, принимают в зависимости от коэффициента
- коэффициент неравномерности нагрузки
по длине зуба, принимают в зависимости от коэффициента ![]() ,
где
,
где ![]() при симметричном расположении колёс
относи-тельно опор ([1], с.13).
при симметричном расположении колёс
относи-тельно опор ([1], с.13).
![]()
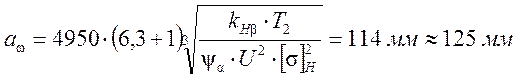 (из стандартного ряда).
(из стандартного ряда).
3.4. Предварительные размеры колеса.
Делительный
диаметр равен 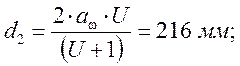
ширина венца ![]()
3.5. Модуль передачи 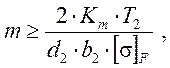 где
где![]() =6,8
для прямозубых колес;
=6,8
для прямозубых колес;![]() =168,96 МПа меньшее
из
=168,96 МПа меньшее
из ![]() и
и ![]() .
.
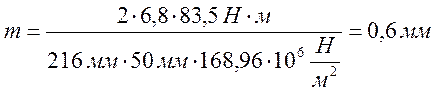 ,
, ![]() .
Пусть m=2.
.
Пусть m=2.
3.6. Угол наклона и суммарное число зубьев.
![]() Суммарное число зубьев
Суммарное число зубьев 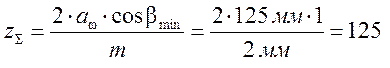 .
.
3.7. Число зубьев шестерни и колеса.
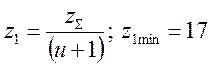 для прямозубых колес ([1], с.14).
для прямозубых колес ([1], с.14). 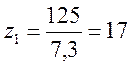 . Число зубьев внеш-него зацепления
. Число зубьев внеш-него зацепления ![]()
3.8. Фактическое передаточное число.
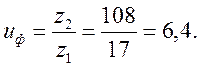
Определим отклонение фактического числа от заданного
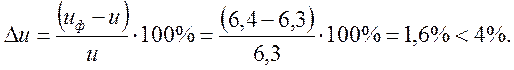
3.9. Диаметры колес.
Делительные
диаметры: шестерни 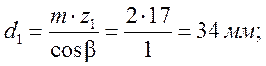
колеса ![]()
Диаметры окружностей вершин и
впадин (da и
df соответственно):
шестерни ![]() колеса
колеса
![]()
3.10. Пригодность заготовок колес.
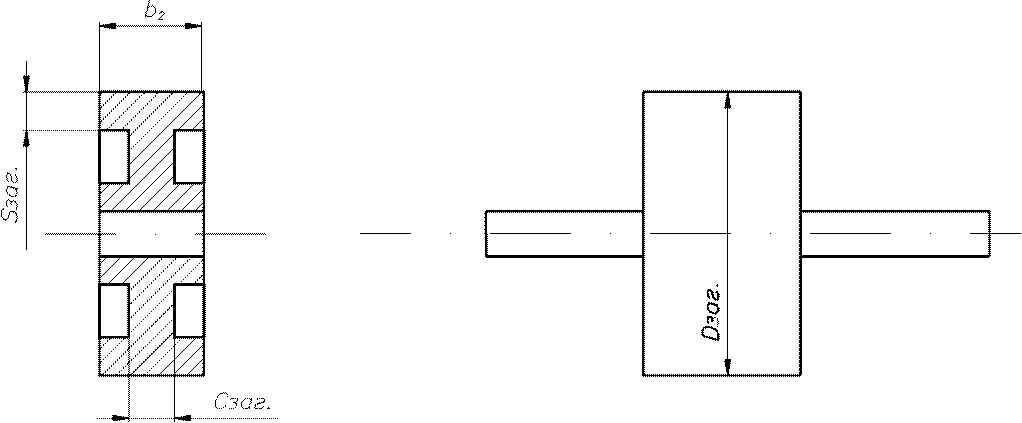 |
рис.2.
Чтобы получить при Т.О. принятые для расчета механические характеристики материала колес, размеры заготовки колес не должны превышать предельно допустимых величин.
Условие
пригодности заготовок колес ![]()
Для
цилиндрической шестерни ![]()
Для колеса с
выточками ![]()
Принимаем
меньшее из этих значений ![]() ([1], табл. 2.1.,
с.10).
([1], табл. 2.1.,
с.10).
44<125 мм – условие выполняется; 16<125 мм – условие выполняется.
3.11. Силы в зацеплении.
Окружная сила
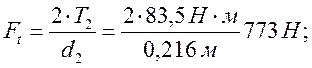
радиальная 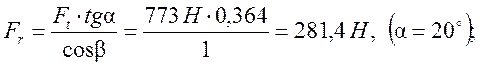
осевая ![]()
3.12. Проверка зубьев по напряжениям изгиба.
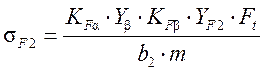 - расчетное напряжение изгиба для
колеса;
- расчетное напряжение изгиба для
колеса;
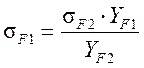 - расчетное напряжение изгиба в
зубьях шестерни.
- расчетное напряжение изгиба в
зубьях шестерни.
![]()
![]() - для прямозубых колес;
- для прямозубых колес;
Из табл. 2.4.
([1], с.19) найдем степень точности в зависимости от окружной скорости
вра-щения колеса ![]() Для данной скорости степень
точности передачи равна 8.
Для данной скорости степень
точности передачи равна 8.
Коэффициент ![]() вычисляем так:
вычисляем так: 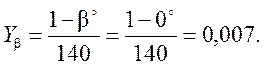
Коэффициент ![]() принимаем по табл. 3.7.([2], с.43):
принимаем по табл. 3.7.([2], с.43): ![]()
![]() , для прямозубых колес при твердости
зубьев ≤350 НВ, принимаем 1,4.
, для прямозубых колес при твердости
зубьев ≤350 НВ, принимаем 1,4.
![]() принимаем по
принимаем по 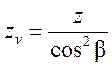 .
Учитывая, что число зубьев колеса
.
Учитывая, что число зубьев колеса ![]() , то
, то ![]() . Тогда из табл. 2.6. ([1], с.16)
. Тогда из табл. 2.6. ([1], с.16) ![]() .
.
![]() – коэффициент формы зуба;
– коэффициент формы зуба;
![]() – коэффициент динамичности
(учитывает динамическое действие нагрузки);
– коэффициент динамичности
(учитывает динамическое действие нагрузки);
![]() – коэффициент концентрации нагрузки
(учитывает неравномерность распределения нагрузки по длине зуба);
– коэффициент концентрации нагрузки
(учитывает неравномерность распределения нагрузки по длине зуба);
![]() – коэффициент наклона зубьев;
– коэффициент наклона зубьев;
![]() – коэффициент распределения нагрузки
между зубьями.
– коэффициент распределения нагрузки
между зубьями.
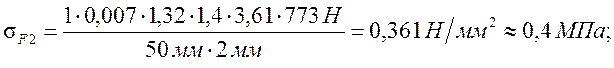
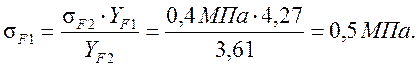
Эти напряжения на изгиб меньше допускаемых. Следовательно, прочность на изгиб колес обеспечена.
3.13. Проверка зубьев колес по контактным напряжениям.
Расчетные
напряжения 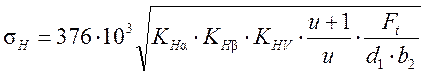 , оно должно быть
, оно должно быть
![]() ,
где
,
где ![]() – коэффициент распределения нагрузки
между зубьями (для прямозу-бых колес
– коэффициент распределения нагрузки
между зубьями (для прямозу-бых колес ![]() =1,0);
=1,0);
![]() – коэффициент концентрации нагрузки.
– коэффициент концентрации нагрузки.
![]() =1,11;
=1,11;
![]() – коэффициент динамичности нагрузки.
– коэффициент динамичности нагрузки.
![]()
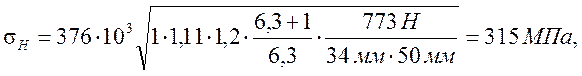 что меньше
что меньше ![]() МПа.
МПа.
4. Расчет открытых передач.
4.1. В моем случае открытой передачей является ременная передача, причем ремень клиновой.
По номограмме ([3], с.83) провожу выбор сечения ремня. Исходя из того, что мощность двигателя Рдв=2,2 кВт и n1= 1425 мин-1 , выбираю ремень клиновой нормального сечения А.
4.2. Определение минимального допускаемого диаметра ведущего шкива.
Из табл. ([3],
с.84) следует, что ![]() . В целях повышения срока
службы ремня бе-ру диаметр шкива на два порядка (размера) выше из стандартного
ряда
. В целях повышения срока
службы ремня бе-ру диаметр шкива на два порядка (размера) выше из стандартного
ряда ![]() .
.
4.3. Определение диаметра ведомого шкива.
![]() – коэффициент скольжения.
– коэффициент скольжения. ![]() .
.
![]() Из стандартного ряда:
Из стандартного ряда: ![]()
4.4. Ориентировочное межосевое
расстояние: ![]() , где h – высота сечения ремня.
, где h – высота сечения ремня.
![]() .
.
4.5. Фактическое передаточное число
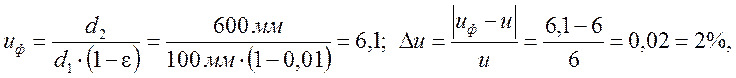
2%<3% – условие выполняется.
4.6. Расчетная длина ремня.
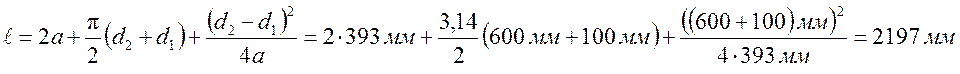
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.