Другие предметы \ Автоматизация производственных процессов

Изучение различий и преимуществ различных систем автоматического управления, страница 5

Z(s) = W1(s) U(s)

Y(s) = W2(s) U(s)

Z(s) » U1(s)

откуда, после исключения промежуточных (относительно Y(s) и U1(s)),величин Z(s) и U(s) получим

WkЭ = W2(s) / W1(s)

где   W2(s)   – передаточная функция объекта по каналу управления т.е. по основному каналу.

        W1(s)   – передаточная функция объекта для расчёта стабилизирующего регулятора, т.е. по вспомогательному каналу.

т.е.

Таким образом видно, что в первом приближении настройки основного регулятора Rк не зависят от вспомогательного регулятора и определяется только WkЭ.


Используя схему рис.5.1, методом Циглера – Никольса проводят расчёт параметров основного ПИД – регулятора.

Рис.5.1.   Структурная схема эквивалентной одноконтурной САР для основного регулятора.

Для настройки основного ПИД – регулятора используются следующие формулы:

Ккр = 7.15

Ткр = 703-268 = 435

П – регулятор:

К = Ккр / 2 = 3,575

ПИ – регулятор:

К = Ккр / 2,2 = 3,25

Тi = 0,83 Ткр = 361,05

К / Тi = 0,009

ПИД – регулятор:

К = 7,15 / 1,65 = 4,33

Тi = 0,5 Ткр = 217,5

Тd = 0,125 Ткр = 54,375

К / Тi = 4,33 / 217,5 = 0,01991

К Тd = 235,44


Рис.5.2.   Переходная характеристика одноконтурной САР с основным регулятором.

Второй этап расчёта:

Он состоит в расчёте настроек вспомогательного регулятора Rст для эквивалентного объекта с передаточной функцией (13), в которую подставляют определённую на предыдущем шаге Rк.

WстЭ(s) = W1(s) + W2(s)Rk(s)

Рис.5.3.   Структурная схема эквивалентной одноконтурной системы регулирования для вспомогательного регулятора


Рис.5.4.   Структурная схема эквивалентной одноконтурной системы с основным ПИД – регулятором и вспомогательным П – регулятором.

В схеме каскадной САР в качестве вспомогательного регулятора используется П – регулятор, рассчитанный по методу Циглера – Никольса:

Ккр = 0,034

П – регулятор:

К = Ккр / 2 = 0,017

Рис.5.5.   Переходная характеристика эквивалентной одноконтурной САР с вспомогательным регулятором.

5.3. Оптимизация каскадной САР.

Оптимизацию проводим используя схему рис.х.  в которую включаем блок "Optim". Варьируемые параметры это коэффициент регулирования и интегральная составляющая основного ПИД – регулятора и коэффициент регулирования вспомогательного П – регулятора. Используя критерии, заданные в блоке "Optim" необходимо добиться улучшения значений показателей качества, например, времени регулирования, перерегулирования или времени достижения первого максимума динамической ошибки и др.

По окончанию процесса оптимизации, используя каждый раз новый критерий оптимизации, в блоках устанавливаются найденные параметры, причём, в исследованной каскадной схеме параметры изменяются на очень малую величину, что совершенно не отражается на переходной характеристике. То есть данная каскадная САР не нуждается в использовании оптимизации.

5.4. Расчёт показателей качества каскадной САР.


Показатели качества рассчитываются по переходной характеристике рис.5.6

Рис.5.6.   Переходная характеристика каскадной САР.

4.  Время регулирования  tр = 1047 с

5.  Время достижения первого максимума tмакс = 419 с.

6.  Время нарастания tн = 257 с

7.  Логарифмический декремент затухания:

8.  Перерегулирование:

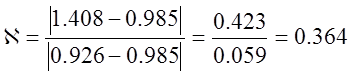
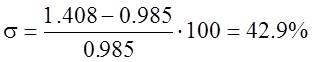
Число колебаний n = 1

Заключение

Курсовое проектирование было нацелено на изучение и более детальное осмысление различий и преимуществ различных систем автоматического управления.

Вначале рассматривались самые простые одноконтурные системы, но как часто бывает простота не означает качество. Существенным фактором при расчётах являлось предположение о низкочастотном характере действующих на объект возмущений, но если это условие не выполняется то регулятор перестаёт работать в оптимальном режиме. Наличие чистого запаздывания и больших постоянных времени также отрицательно влияют на систему, причём, даже при оптимальных настройках регуляторов одноконтурные САР характеризуются большими динамическими ошибками, низкой частотой регулирования, длительными переходными процессами.

Поэтому в систему были введены дополнительные контура регулирования, то есть рассматривались многоконтурные системы. Комбинированные САР компенсировали значительные возмущающие воздействия, что позволила существенно снизить динамическую ошибку регулирования.

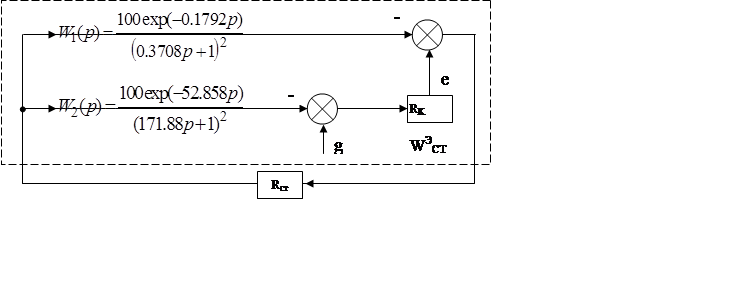
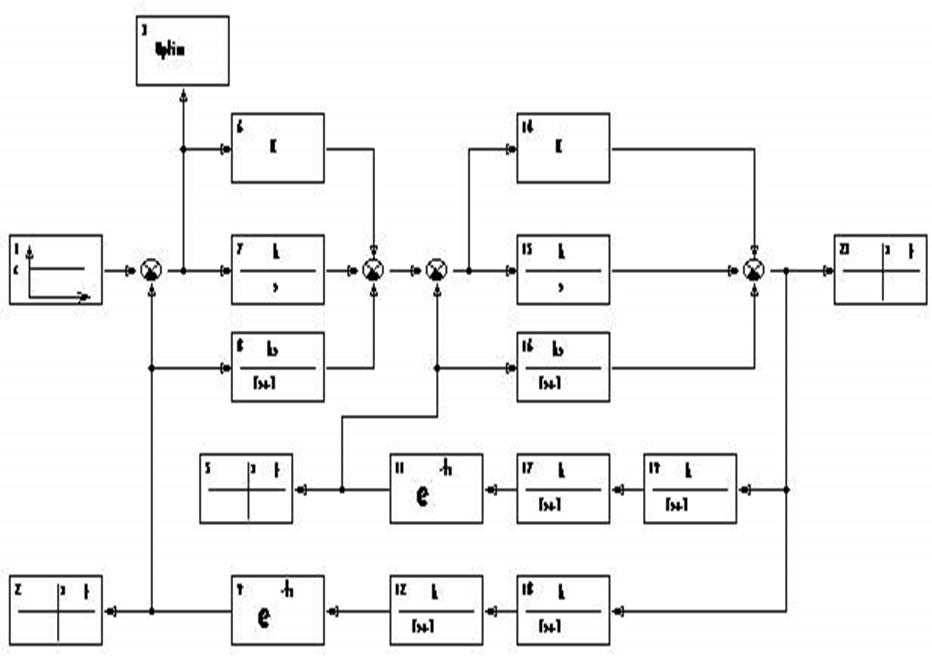
Дальнейшим рассмотрением схем с компенсацией возмущения по упреждающей цепи являются системы каскадного регулирования. Дополнительный регулятор осуществляет регулирование некоторой промежуточной регулируемой величины в местном контуре регулирования, в работу которого вмешивается нежелательное возмущение. Влияние возмущения на основную регулируемую величину будет тем меньше, чем выше быстродействие вспомогательного контура по отношению к основному, то есть повышается качество переходного процесса.

В заключение отметим, что из трёх рассматриваемых схем наиболее лучшей является схема каскадного регулирования.

Литература

1.  Балабанов А.А. Локальные системы автоматики. – Кишинёв: УТМ, 1995. – 127 с.

2.  Балабанов А.А. Проектирование, моделирование и расчёт систем локальной автоматики. – Кишинёв: ТУМ, 1995. – 35 с.

3.  Курсовое и дипломное проектирование по автоматизации производственных процессов / Под ред. И. К. Петрова.-М.: Высш.школа,1986.-352 с.

4.   Воронов А.А. Теория автоматического регулирования. – М.: Высшая школа, 1977. – 453 с.

Скачать файл