Министерство путей сообщения
Российской Федерации
Дальневосточный государственный
университет путей сообщения
Забайкальский институт
железнодорожного транспорта
Кафедра “ЭТиФ”
П.Ю. Лукьянов
А.Г. Машкин
Г.Н. Бурнашов
А.А. Лукьянова
Н.В. Коноплева
ЛАБОРАТОРНЫЕ РАБОТЫ ПО ДИСЦИПЛИНЕ "МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НА ЭВМ"
ЧАСТЬ I
Методические указания
Чита
2000
ЛАБОРАТОРНАЯ РАБОТА № 1. МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ТЕЛ В ВЯЗКИХ ЖИДКОСТЯХ.
1.1. Цель работы
Получение практических навыков разработки математических моделей механических систем и моделирования на ЭВМ процессов в механических системах.
1.2. Теоретическая часть
В работе рассматривается движение тела в вязкой жидкости с учетом следующих сил:
· силы тяжести;
· архимедовой силы;
· силы жидкостного трения при ламинарном или турбулентном обтекании тела.
В базовой математической модели рассматривается только вертикальное движение тела (шара). Шар, имеющий массу M, движется в вязкой жидкости (плотность жидкости p). Начальная вертикальная скорость шара равна V0 и соответствует моменту времени t=0.
Базовая математическая модель системы
На шар, движущийся вертикально в жидкости, действуют три силы - сила тяжести Fg, архимедова сила Fa и сила трения Ft. Сумма всех действующих на тело сил равна произведению массы тела M на его ускорение a, т.е.
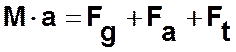
Далее будем считать, что координатная ось направлена вертикально вниз. Сила тяжести при таком направлении координатной оси будет положительной, архимедова сила - отрицательной, а знак силы трения будет противоположным знаку скорости. Сила тяжести Fg равна Mg, где g-ускорение свободного падения, архимедова сила Fa равна -gpW, где W-объем тела. В случае ламинарного обтекания тела зависимость между скоростью тела и силой трения представляет собой прямую пропорциональность, т.е. Ft=-b*V, где b-коэффициент пропорциональности. Знак при b определяется тем, что сила трения направлена противоположно скорости V. В другом крайнем случае, при турбулентном обтекании, зависимость между Ft и V квадратичная, или, с учетом направления силы трения,
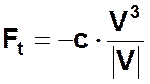
Коэффициенты пропорциональности b и c зависят от размеров и формы тела, плотности и вязкости жидкости и являются внешними для данной модели. Т.к. ускорение является производной от V(t) по времени, т.е. a=dV(t)/dt, после подстановки выражений для действующих сил в уравнение движения тела получаем следующие обыкновенные дифференциальные уравнения:
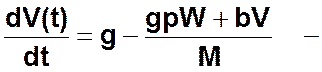
для случая ламинарного обтекания, и
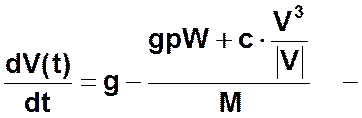
для случая турбулентного обтекания тела жидкостью.
Эти дифференциальные уравнения могут быть численно проинтегрированы на ЭВМ с использованием одного из следующих численных методов: простого метода Эйлера 1-го порядка, модифицированного метода Эйлера 2-го порядка или метода Рунге-Кутты 4-го порядка.
Задачей Коши для полученных дифференциальных уравнений является начальное условие вида V(t0)=V0. Последнее условие позволяет получить частное решение дифференциального уравнения, т.е. однозначно определить все параметры, описывающие поведение системы, как функции от времени.
1.3. Порядок выполнения работы
1. Разработать математическую модель системы в соответствии с индивидуальными заданиями и программу для моделирования процессов в системе с выводом на экран монитора в графической форме следующих зависимостей:
а) V(t);
б) V'(V).
2. Изучить процессы в системе и качественно определить зависимости параметров, характеризующих процессы в системе (времена процессов в системе, максимальные и средние скорости и ускорения) от значений M, p, W, b, c и V0 в следующих случаях:
а) V0=0 ;
б) V0<>0.
(В качестве базовых значений параметров M, p, W, b,c и V0 принять M=1кг, p=1000кг/куб.м, W=0.001куб.м, b=1, c=1 и V0=1м/с.)
3. Для каждого случая, рассмотренного в п.2, зарисовать зависимости V(t) и V'(V) и объяснить наблюдаемые эффекты.
4. Смоделировать влияние вертикальных движений жидкости для зависимостей Vl(t) согласно индивидуальным заданиям и качественно объяснить изменение вида V(t) и фазовых траекторий.
ЛАБОРАТОРНАЯ РАБОТА № 2. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ПОСЛЕДОВАТЕЛЬНОМ RL- КОНТУРЕ.
1.1. Цель работы
Получение практических навыков моделирования на ЭВМ процессов в электрических системах на примере последовательного RL- контура.
1.2. Теоретическая часть
Электрическая схема контура представлена на рис.1.
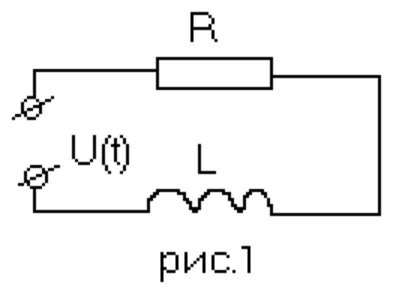
Базовая математическая модель системы
Исходя из второго закона Кирхгофа (сумма падений напряжения на элементах контура равна сумме ЭДС) имеем:
![]()
где UL(t) и UR (t) - неизвестные функции, описывающие падение напряжения на индуктивности L и активном сопротивлении R соответственно в зависимости от времени. Выразим UL(t) и UR(t) через неизвестную функцию I(t), описывающую зависимость контурного тока от времени. Т.к.
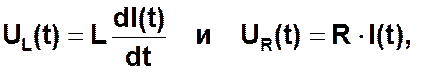
получаем:

Разделив обе части уравнения на L и перенося в правую часть уравнения слагаемые, в которые не входит производная dI(t)/dt, получим обыкновенное дифференциальное уравнение:
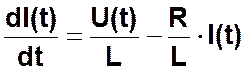
Это дифференциальное уравнение может быть численно проинтегрировано на ЭВМ с использованием одного из следующих численных методов: простого метода Эйлера 1-го порядка, модифицированного метода Эйлера 2-го порядка или метода Рунге-Кутты 4-го порядка. Оптимальный порядок численного метода определяется исходя из максимального порядка непрерывных производных по времени t от правой части дифференциального уравнения в зависимости от вида U(t).
Задачей Коши для данного дифференциального уравнения является начальное условие вида I(t0)=I0. Последнее условие позволяет получить частное решение дифференциального уравнения, т.е. однозначно определить все параметры, описывающие поведение системы, как функции от времени.
1.3. Порядок выполнения работы
1. Разработать математическую модель системы в соответствии с индивидуальными заданиями и программу для моделирования процессов в системе с выводом на экран монитора в графической форме следующих зависимостей:
а) I(t);
б) U(t);
в) UR(t);
г) UL(t);
д) I'(I);
е) A(w) (частотный спектр для I(t)).
2. Изучить процессы в системе и качественно определить зависимости параметров, характеризующих процессы в системе (амплитудные значения токов, относительные амплитуды гармоник, характерные времена и частоты, и т.д.) от значений R, L, U0, I0, w и вида U(t) в указанных ниже случаях. В качестве базовых значений параметров R, L, I0, U0, dt, Log2NP и w принять R=1Oм, L=1Гн, I0=1А, U0=1В, dt=0.01с, Log2NP=10 и w=3рад/с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.