а) U(t)=0, I0<>0;
б) U(t)<>0, I0=0;
б.1) U(t)=U0*cos(w*t);
б.2) U(t)=U0*(1+cos(w*t));
б.3) U(t) - симметричный относительно оси t меандр со скважностью 2, циклической частотой w и амплитудой U0. Для вычисления U(t) использовать оператор
if(odd(trunc(w*t/pi))) then U:=U0 else U:=-U0;
б.4) U(t) - меандр со скважностью 2, циклической частотой w, амплитудой U0 и постоянной составляющей, равной U0. Для вычисления U(t) использовать оператор
if(odd(trunc(w*t/pi))) then U:=2*U0 else U:=0;
б.5) U(t) - пилообразная функция с циклической частотой w и амплитудой U0 без постоянной составляющей. Для вычисления U(t) использовать оператор U:=2*U0*(frac(w*t/(2*pi))-0.5);
б.6) U(t) - пилообразная функция с циклической частотой w и амплитудой U0 c постоянной составляющей U0. Для вычисления U(t) использовать оператор U:=U0+2*U0*(frac(w*t/(2*pi))-0.5);
в) U(t)<>0 и I0<>0 для U(t) видов, рассмотренных в п.п. б.1-б.6.
3. Для каждого случая, рассмотренного в п.2, зарисовать зависимости I(t), I'(I) и A(w) и объяснить наблюдаемые эффекты.
ЛАБОРАТОРНАЯ РАБОТА № 3. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ПОСЛЕДОВАТЕЛЬНОМ RLC- КОНТУРЕ.
1.1. Цель работы
Получение практических навыков моделирования на ЭВМ процессов в электрических системах на примере последовательного RLC-контура.
Теоретическая часть
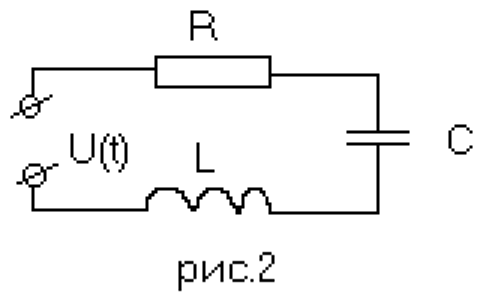
Электрическая схема контура представлена на рис.2.
Базовая математическая модель системы
Исходя из второго закона Кирхгофа (сумма падений напряжения на элементах контура равна сумме ЭДС) имеем:
![]()
где UL(t), UR(t) и UC(t) - неизвестные функции, описывающие падение напряжения на индуктивности L, активном сопротивлении R и емкости C соответственно в зависимости от времени. Выразим UL(t), UR(t) и UC(t) через неизвестную функцию I(t), описывающую зависимость контурного тока от времени. Т.к.
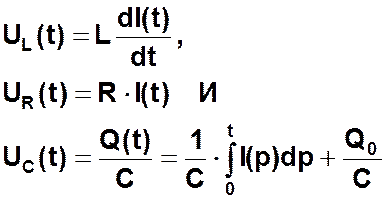
где Q-заряд, накопленный на обкладках конденсатора в момент времени t, а Q0 - начальный заряд (при t=0) на обкладках конденсатора, получаем:
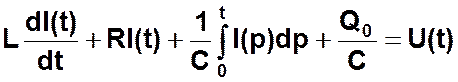 |
Продифференцировав обе части уравнения по времени и разделив обе части уравнения на L, получим линейное дифференциальное уравнение 2-го порядка:
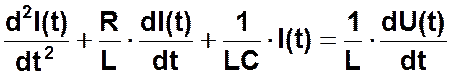
Это дифференциальное уравнение может быть сведено к системе из двух обыкновенных дифференциальных уравнений и затем численно проинтегрировано на ЭВМ с использованием одного из следующих численных методов: простого метода Эйлера 1-го порядка, модифицированного метода Эйлера 2-го порядка или метода Рунге-Кутты 4-го порядка для систем дифференциальных уравнений. Оптимальный порядок численного метода определяется исходя из максимального порядка непрерывных производных по времени t от правых частей дифференциальных уравнений системы в зависимости от вида U(t). Для сведения полученного дифференциального уравнения 2-го порядка к системе обыкновенных дифференциальных уравнений введем функцию
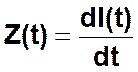
Производная от функции Z(t) по времени будет равна
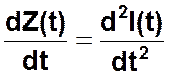
Производя замены первой и второй производных от I(t) в дифференциальном уравнении на Z(t) и ее производную, далее перенося все члены уравнения, не содержащие производных от неизвестных функций, в правую часть, получим первое уравнение системы. В качестве второго уравнения системы можно взять равенство, связывающее Z(t) и I(t). Система обыкновенных дифференциальных уравнений в виде, позволяющем проводить численное интегрирование одним из названных выше методов, выглядит так:
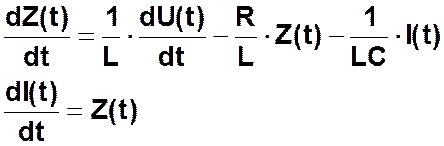
Задачей Коши для данной системы дифференциальных уравнений является пара начальных условий вида Z(t0)=Z0 и I(t0)=I0. Последние позволяют получить частное решение системы дифференциальных уравнений, т.е. однозначно определить все параметры, описывающие поведение системы, как функции от времени.
1.3. Порядок выполнения работы
1. Разработать математическую модель системы в соответствии с индивидуальными заданиями и программу для моделирования процессов в системе с выводом на экран монитора в графической форме следующих зависимостей:
а) I(t);
б) U(t);
в) UL(t);
г) UC(t);
д) I'(I);
е) A(w) (частотный спектр для I(t)).
2. Изучить процессы в системе и качественно определить зависимости параметров, характеризующих процессы в системе (амплитудные значения токов, относительные амплитуды гармоник, характерные времена и частоты и т.д.) от значений R, L, C, U0, Z0, I0, w и вида U(t) в указанных ниже случаях. В качестве базовых значений параметров R, L, C, Z0, I0, U0, dt, Log2NP и w принять R=1Oм, L=1Гн, C=1Ф, Z0=0А/c, I0=1А, U0=1В, dt=0.01с, Log2NP=11 и w=3рад/с.
а) U(t)=0, I0<>0, Z0=0;
б) U(t)=0, I0=0, Z0<>0;
в) U(t)<>0, I0=0, Z0=0;
в.1) U(t)=U0*cos(w*t);
в.2) U(t)=U0*(1+cos(w*t));
в.3) U(t)-симметричный относительно оси t меандр со скважностью 2, циклической частотой w и амплитудой U0. Для вычисления U(t) использовать оператор
if(odd(trunc(w*t/pi))) then U:=U0 else U:= - U0;
в.4) U(t) - меандр со скважностью 2, циклической частотой w, амплитудой U0 и постоянной составляющей, равной U0. Для вычисления U(t) использовать оператор
if(odd(trunc(w*t/pi))) then U:=2*U0 else U:=0;
в.5) U(t) - пилообразная функция с циклической частотой w и амплитудой U0 без постоянной составляющей. Для вычисления U(t) использовать оператор
U:=2*U0*(frac(w*t/(2*pi))-0.5);
в.6) U(t) - пилообразная функция с циклической частотой w и амплитудой U0 c постоянной составляющей U0. Для вычисления U(t) использовать оператор
U:=U0+2*U0*(frac(w*t/(2*pi))-0.5);
г) U(t)<>0, I0<>0 и Z0=0 для U(t) видов, рассмотренных в п.п. в.1-в.6.
д) Отдельно рассмотреть возникающие эффекты при следующих соотношениях параметров:
д.1) I0=0, Z0=0, R=0, U(t)=U0*cos(w*t) и w=w0, где w02=1/LC (резонанс);
д.2) I0<>0, Z0=0, R=0, U(t)=U0*cos(w*t) и w=e*w0, где e-величина, близкая к единице (e=0.8..1.2) (амплитудные биения);
д.3) I0<>0, R<<w0*L, R<<1/(w0*C), U(t)=U0*cos(w*t) и w=e*w0 (длительный переходный процесс, сопровождающийся затухающими амплитудными биениями);
д.4) I0=0, R<<w0*L, R<<1/(w0*C), U(t) – любая периодическая негармоническая функция без постоянной составляющей и n*w=e*w0, где n-небольшое натуральное число (n=2..5). Определить зависимость амплитуды тока для установившегося процесса от w или e (резонанс на гармонике).
3. Для каждого случая, рассмотренного в п.2, зарисовать зависимости I(t), UL(t), UC(t), I'(I) и A(w) и объяснить наблюдаемые эффекты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.