Другие предметы \ Математическое моделирование систем и процессов

Математическое моделирование систем и процессов. Часть 4: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 5

, (12.10)

и сделаем подстановку его в уравнение (12.9):

(12.11)

6. Проинтегрируем выражение (12.11) и сгруппируем в правой части члены полученного уравнения, не содержащие производных:

. (12.12)

7. Введем обозначение:

(12.13)

и сделаем подстановку его в уравнение (12.12):

(12.14)

8. Проинтегрируем уравнение (12.14) и из полученного соотношения выразим :

. (12.15)

9. Объединив (12.15), (12.13) и (12.10), получим систему уравнений состояния:

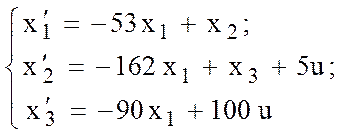(12.16)

или в векторно-матричной форме:

(12.17)

где

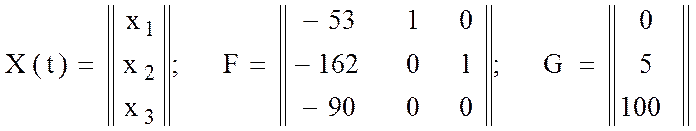12.3. Информация к выполнению задания 2

Пример выполнения задания 2

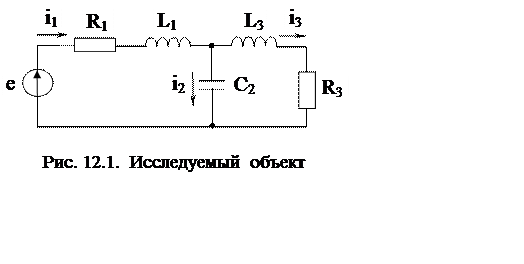Исследуемый объект − линейная электрическая цепь 3-го порядка (рис. 12.1). Сформировать математическую модель данного объекта в пространстве состояний.

1. В качестве переменных состояния принимаем:

(12.18)

Следовательно, вектор состояния:

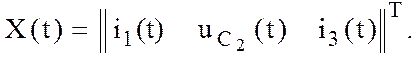(12.19)

2. На основании законов Кирхгофа формируем систему уравнений, количество которых должно быть равно порядку моделируемого объекта:

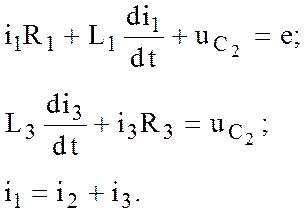(12.20)

3. Исключаем все неизвестные, не являющиеся переменными состояния.

Для этого ток i₂ выразим через :

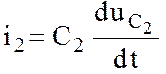(12.21)

и делаем подстановку его в систему (12.20):

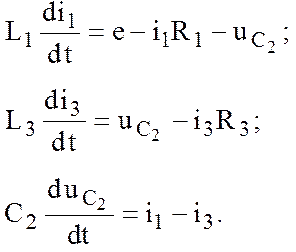(12.22)

4. Приводим систему (12.22) к нормальной форме и записываем уравнения в порядке, соответствующем расположению переменных состояния в векторе состояния (12.19):

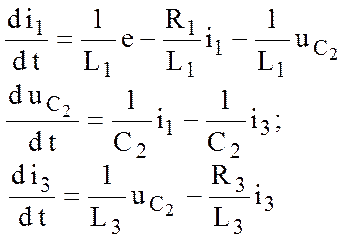(12.23)

или в векторно-матричной форме:

(12.24)

где

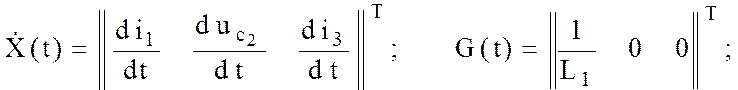
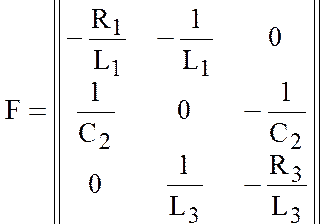; u(t) = e

при заданных начальных условиях:

. (12.25)

12.4. Информация к выполнению задания 3

Пример выполнения задания 2

Решение математической модели (12.24).

1. Задание параметров электрической цепи:

2. Решение задачи Коши с помощью встроенной функции rkfixed:

Начальный вектор состояния:

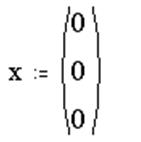
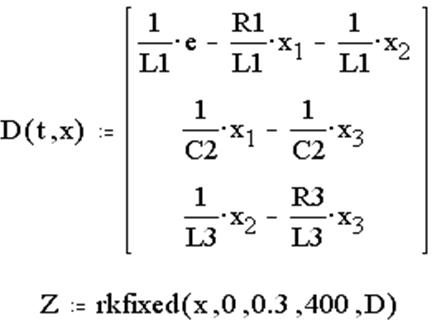
3. Вывод матрицы решения Z:

4. Графическое отображение решения модели (12.24):

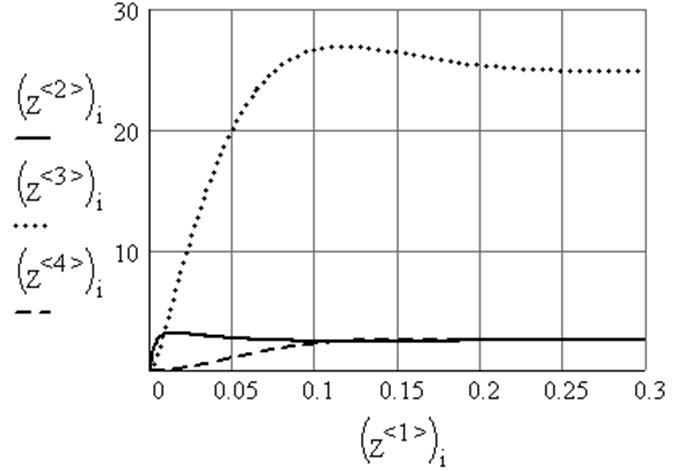
5. Построение фазовой траектории исследуемого объекта (рис. 12.1) :

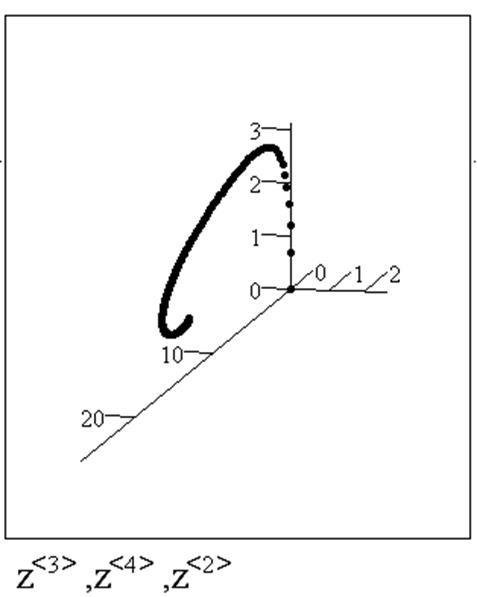
12.5. Задания

1. Для линейной непрерывной стационарной системы задана математическая модель в форме передаточной функции W(p) (табл. 12.1). Сформировать два варианта математической модели данной физической системы в пространстве состояний:

а) на основе полюсов передаточной функции;

б) на основе дифференциального уравнения, соответствующего заданной передаточной функции.

2. Для заданного объекта − электрической цепи (табл. 12.2) сформировать математическую модель в пространстве состояний.

3. Решить сформированную модель с помощью встроенной функции rkfixed. Решение представить графически для отображения динамики изменения каждой переменной состояния x_i исследуемого объекта.

4. Построить фазовую траекторию для отображения изменения состояния исследуемого объекта во времени.

5. Ответить на контрольные вопросы:

а) для физических систем какого класса передаточные функции в форме изображений Лапласа и в операторной форме совпадают?

б) почему задача определения нулей и полюсов передаточной функции имеет особо важное значение при исследовании объектов и систем ?

в) при каких условиях передаточные функции W(s) и W(p) могут достоверно описывать исследуемую физическую систему?

г) как определить порядок будущей модели в пространстве состояний, если известна передаточная функция исследуемого объекта?

Таблица 12.1

Математические модели в форме передаточных функций

Вариант	Передаточная функция W(p)	Вариант	Передаточная функция W(p)
1	2	4	3
1		8
2		9
3		10
4		11
5		12
6		13
7		14

Таблица 12.2

Исходные данные к заданию 2

Вариант

Исходные данные

Объект-оригинал

Продолжение табл. 12.2

6
7
8
9
10
11

Окончание табл. 12.2

1	2	3
12
13

Библиографический список

1. Дьяконов В. П. Энциклопедия Mathcad 2001i и Mathcad 11 / В. П. Дьяконов М.: СОЛОН-пресс, 2004. 832 с.

2. Голубева Н. В. Основы математического моделирования систем и процессов: Учебное пособие / Н. В. Голубева / Омский гос. ун-т путей сообщения, Омск, 2006. 96 с.

3. Колдаев В. М. Численные методы и программирование: Учебное пособие / В. М. Колдаев. М.: ИД «Форум»: ИНФРА-М, 2008. 336 с.

4. Вержбицкий В. М. Основы численных методов: Учебник для вузов / В. М. Вержбицкий. М.: Высшая школа, 2002. 840 с.

5.Смирнов В. И. Курс высшей математики. Том 1: / В. И. Смирнов. СПб.: БВХ-Петербург, 2008. 642 с.

6. Мирошник И. В. Теория автоматического управления. Линейные системы / И.В. Мирошник. СПб: Питер, 2005. 336 с.

Учебное издание

ГОЛУБЕВА Нина Викторовна

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

СИСТЕМ И ПРОЦЕССОВ

Часть 4

Редактор Т. С. Паршикова

* * *

Подписано в печать .06.200. Формат 6084 .

Плоская печать. Бумага офсетная. Усл. печ. л. 2,0. Уч.- изд. л. 2,2.

Тираж 600 экз. Заказ .

* *

Редакционно-издательский отдел ОмГУПСа

Типография ОмГУПСа

644046, г. Омск, пр. Маркса, 35

1 2 3 4 5

Скачать файл