Другие предметы \ Математическое моделирование систем и процессов

Математическое моделирование систем и процессов. Часть 4: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 4

1

2

3

4

3

11

4

12

5

13

6

14

7

15

8

16

Таблица 11.2

Исходные данные для численного интегрирования функции,

заданной  таблично

Вариант

Узловые значения  xi  и

 значения  подынтегральной  функции yi  в  узлах

1

2

1

x = {1;  1,5;  2;  2,5;  3;  3,5;  4;  4,5;  5;  5,5;  6;  6,5; 7}

y = {15,4;  4,7;  1;  8,9;  28,4;  18;  15,5;  1;  3;  5,3;  11;  2;  4,1}

2

x = {7;  8,1;  9,2;  10,3;  11,4;  12,5;  13,6;  14,7;  15,8;  16,9; 18}

y = { 9,8;  1,2;  6;  3,5;  1,9;  4,4;  11;  8,2;  1,3; 9; 17}

3

x = {0,1;  0,5;  0,9;  1,3;  1,7;  2,1;  2,5;  2,9;  3,3;  3,7;  4,1}

y = {0,4;  7,2;  1,7;  22;  7,9;  11,5;  4,9;  8;  1,4;  0,7;  12}

Окончание табл. 11.2

1

2

4

x = {5;  6,15;  7,3;  8,39; 10;  10,7;  12,3;  12,8;  13}

y = {13,312;  8,7;  −5,07;  −7,973;  −8,74;  2,5;  4,25;  13;  8,33}

5

x = {3;  3,5;  4;  4,5;  5,5;  6,5;  7;  7,5;  8;  8,5;  9}

y = {14,3;  6,1;  7;  33,4;  8,7;  2;  19,2;  7,1; 11;  37;  20}

6

x = {2,6;  4,8;  7;  9,2;  11,4;  13,6;  15,8;  18;  20,2}

y = {5;  0,7;  1,8;  4,6;  12, 1;  5;  14,9;  3,5;  0,3}

7

x = {5;  5,3;  5,6;  5,9;  6,2;  6,5;  6,8;  7,1;  7,4;  7,7;  8}

y = {25;  12,  8,8;  0,7;  11,5;  1,7;  17;  0,9;  1, 4;  4;  7,1}

8

x = {0,2;  0,8;  1,4;  2;  2,6;  3,4;  4;  4,6;  5,2;  5,8;  6,4}

y = {1,2;  2,9;  19;  1,8;  11,7;  32,9;  23;  5;  17,1;  4;  15,2}

9

x = {1;  1,5;  2;  2,5;  3;  3,5;  4;  4,5;  5;  5,5;  6;  6,5;  7}

y = {17;  5,1;  3;  16,7;  7,2;  2,5;  27;  1,5;  17,2;  8;  0,2;  6,1;  13}

10

x = {7,5;  7,8;  8,1;  8,4;  8,7;  9;  9,3;  9,6;  9,9;  10,2;  10,5}

y = {31,2;  17,3;  4,5;  9,9;  2;  7,5;  25;  11,2;  42;  11,8;  3,7}

x = {1,3;  1,9;  2,5;  3,1;  3,7;  4,3;  4,9;  5,5;  6,1;  6,7;  7,3}

y = {3,9;  1,7;  9,9;  13;  5,4;  10,5;  25;  13,1;  2;  8,2;  7}

11

12

x = {3;  3,5;  4;  4,5;  5,5;  6,5;  7;  7,5;  8;  8,5;  9;  9,5;  10}

y = {3,6;  1,3;  7;  4,2;  7,8;  7;  19;  6,1;  4,8;  18,1;  10;  15,5;  7}

13

x = {5,9;  7  8,1;  9,2;  10,3;  11,4;  12,5;  13,6;  14,7;  15,8;  16,9}

y = {0,6;  29;  10,4;  2,1;  15,7;  6,3;  1;  3,16;  16,9;  27;  4,8}

14

x = {0,9;  1,3;  1,7;  2,1;  2,5;  2,9;  3,3;  3,7;  4,1;  4,5;  4,9}

y = {25;  10;  5,4;  1,5;  7,8;  15,3;  3;  8,8;  1,9;  29;  21,5}

15

x = {0,8;  1,4;  2;  2,6;  3,4;  4;  4,6;  5,2;  5,8;  6,4;  7;  7,6;  8,2}

y = {6,1;  13,3;  37;  8;  1,8;  9,3;  25;  12,7;  7;  28,5;  11;  3,3;  7}

16

x = {5,9;  6,2;  6,5;  6,8;  7,1;  7,4;  7,7;  8;  8,3;  8,6;  8,9}

y = {7;  2,9;  9;  2,7;  11,7;  5,8;  11;  25,1;  10;  14;  1,8}

Лабораторная  работа  №  12

МАТЕМАТИЧЕСКИЕ  МОДЕЛИ  В  ПРОСТРАНСТВЕ  СОСТОЯНИЙ,

ИХ  ВЗАИМОСВЯЗЬ  С  МОДЕЛЯМИ  В  ФОРМЕ  ПЕРЕДАТОЧНЫХ  ФУНКЦИЙ  И  ДИФФЕРЕНЦИАЛЬНЫХ  УРАВНЕНИЙ.

12.1.Постановка  задачи

Описание объектов и процессов с помощью математического аппарата пространства состояний широко используется в теории систем, в теории автоматического управления, в радиотехнике и связи, в электротехнике и многих других областях. Моделирование в пространстве состояний обеспечивает широкие возможности при решении задач анализа, синтеза и проектирования систем различной физической природы. Метод пространства состояний обладает следующими достоинствами:

возможностью с единой позиции рассматривать стационарные и нестационарные, линейные и нелинейные системы;

возможностью учитывать ненулевые начальные условия;

наличием достаточного количества численных методов реализации таких математических  моделей;

возможностью более разностороннего изучения физической системы путем формирования нескольких  моделей  в разных пространствах состояний.

          В данной работе рассматриваются различные способы формирования  математических моделей в пространстве состояний, в том числе по передаточной функции исследуемой системы, по ее дифференциальному уравнению. Решается задача моделирования объекта − электрической цепи с помощью математического аппарата пространства состояний. Уделяется внимание особенностям решения моделей такого класса средствами системы  MathCAD.

12.2. Информация  к  выполнению  задания  1

          Встроенная функция polyroots(Ak) вычисляет корни полинома. Параметр функции Ak – вектор, составленный из коэффициентов полинома а0, а1, а2, … , аn. Результатом функции  является вектор, состоящий из n корней полинома.

          Пример выполнения задания 1. а

          Пусть для линейной непрерывной стационарной системы задана математическая  модель  в форме передаточной  функции:

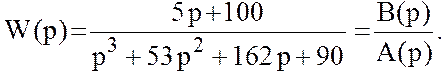                           (12.1)

Сформировать для  данной физической системы  математическую модель в пространстве  состояний  на основе полюсов передаточной функции.

          1. Формирование  вектора  коэффициентов  полинома :

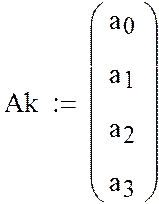
2. Определение корней характеристического уравнения , т. е. полюсов  передаточной  функции :

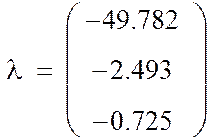
3. Запись модели  в пространстве состояний  в общем виде:

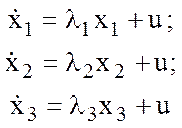                                               (12.2)

или  ввекторно-матричной форме:

                                        (12.3)

где

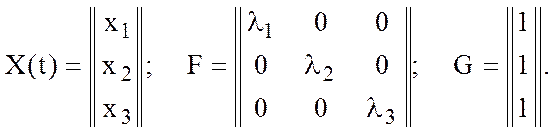
          4. Подстановка  числовых  значений  полюсов в (12.2):

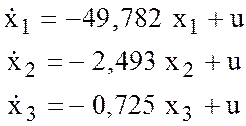,                                         (12.4)

где

.

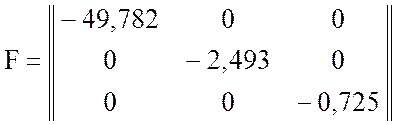          Пример выполнения задания 1. б

          Линейная непрерывная стационарная система описана передаточной функцией (12.1). Сформировать модель в пространстве состояний по дифференциальному  уравнению, соответствующему  данной передаточной функции.

          1. Перейдем от передаточной функции к  дифференциальному уравнению в операторной  форме:

A(p)y(t)=B(p)u(t)                                (12.5)

или

.               (12.6)

          2. Представим  дифференциальное уравнение (12.5) в обычной  форме:

.           (12.7)

          3. Введем обозначение y(t) = x1(t) = x1  и сделаем подстановку его в уравнение (12.7):

.                      (12.8)

          4. Сгруппируем члены уравнения (12.8), не содержащие производных, в  правой части  уравнения:

.                   (12.9)

          5. Введем обозначение:

Скачать файл