Математическое моделирование систем и процессов. Часть 4: Методические указания к выполнению лабораторных работ и самостоятельной работы

Н. В. ГОЛУБЕВА

МАТЕМАТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  СИСТЕМ  И

  ПРОЦЕССОВ

ЧАСТЬ  4

ОМСК  2009

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

_________________________

Н. В. Голубева

МАТЕМАТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  СИСТЕМ  И

  ПРОЦЕССОВ

Часть  4

Утверждено редакционно-издательским советом  университета

в качестве  методических  указаний  к выполнению лабораторных  работ  и

самостоятельной  работы  по дисциплине

 «Математическое  моделирование систем  и процессов»

Омск  2009

ОГЛАВЛЕНИЕ

Введение ……………………………………………………………….....	5
Лабораторная работа 11. Численное интегрирование ……………………	6
11.1. Постановка задачи………..……………………………………..	6
11.2.Обзор классических  методов численного интегрирования......	8
11.3. Метод Монте-Карло (метод статистических испытаний) …...	12
11.4. Информация к выполнению задания1 ………………………..	14
11.5. Информация к выполнению задания2 ………………………..	15
11.6. Информация к выполнению задания3 ………………………..	16
11.7. Информация к выполнению задания4 ………………………..	17
11.8. Задания ………………………………………………………….	20
Лабораторная работа 12. Математические  модели  в пространстве состояний, их взаимосвязь с моделями в форме передаточных функций и  дифференциальных  уравнений……………………………………….	23
12.1. Постановка  задачи ……………………………………………..	23
12.2. Информация к выполнению задания1 ……………………….	23
12.3. Информация к выполнению задания 2 ……………..................	26
12.4. Информация к выполнению задания 3 ……………..................	28
12.5. Задания …………………………………………….....................	30
Библиографический список………………………...……………….........	34

ВВЕДЕНИЕ

Инструментом исследования процессов и устройств различной физической природы, в том числе в энергетике, электротехнике, на железнодорожном транспорте, в автоматике, в системах управления и связи, является математическое моделирование. Перспективы и возможности математического  моделирования при решении научно-технических и инженерных задач существенно возрастают с внедрением новых  информационных технологий, с появлением мощных компьютерных математических систем и пакетов.

Данные методические указания, представляют четвертую часть комплекта  учебно-методических разработок по дисциплине «Математическое моделирование систем и процессов». Они включают в себя две лабораторные работы. Лабораторная работа 11 посвящена задаче численного интегрирования. Рассматриваются детерминированные и стохастические методы решения, алгоритмы оценивания их методической погрешности, особенности их реализации в системе MathCAD. В лабораторной работе 12 рассматриваются математические модели в пространстве состояний, приемы их формирования по заданным передаточным функциям или дифференциальным уравнениям, особенности их решения средствами системы MathCAD.

В процессе выполнения лабораторных работ студент должен уяснить важность правильной постановки задачи, выбора метода ее решения и способа отображения результатов моделирования и умения правильно интерпретировать их.

Методические указания предназначены для студентов 2-го курса очного и заочного обучения, а также для обучения с использованием  дистанционных образовательных технологий.

Лабораторная  работа  11

ЧИСЛЕННОЕ   ИНТЕГРИРОВАНИЕ

11.1.Постановка  задачи

Решение многих научных и инженерных задач на разных этапах приводит к необходимости вычисления значения определенного интеграла. К интегрированию функций сводятся задачи нахождения площадей и объемов, вычисления пути, пройденного точкой при неравномерном движении, определения центров тяжести и моментов инерции тел, работы, произведенной некоторыми  силами и  многие другие.

Если функция f(x) непрерывна на отрезке  и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от а  до b может быть  вычислен  по формуле Ньютона-Лейбница

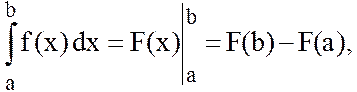                                 (11.1)

где 

          Однако на практике только для ограниченного числа подынтегральных функций  f(x) удается воспользоваться формулой (11.1) и найти аналитическое решение, то есть выразить первообразную в виде комбинации алгебраических и трансцендентных функций. 

В большинстве задач первообразную F(x) не удается выразить через элементарные функции или  же она получается чрезмерно сложной. Кроме того, функция f(x) часто задается в виде таблицы ее значений на фиксированном  конечном  множестве точек   и, следовательно, теряет смысл само понятие первообразной.  В  этих случаях  применяются  методы численного интегрирования.

В основу классических методов  численного интегрирования  положено  геометрическое  толкование определенного  интеграла как площади криволинейной  трапеции, ограниченной  кривой  y = f(x), осью абсцисс и прямыми  x = a  и  x = b (рис. 11.1).

          Задача  численного интегрирования состоит в нахождении приближенного значения определенного интеграла с помощью некоторой приближенной формулы через известные значения подынтегральной  функции f(x) (а иногда и ее производных) в заданных точках. Такие формулы называются  квадратурными (“квадратура” происходит от латинского слова  quadratura – вычисление площади  или  квадрирование).

          Квадратурная формула позволяет искомый интеграл заменить определенной линейной комбинацией (линейной функцией) значений подынтегральной  функции  в  n + 1 точках  интервала :

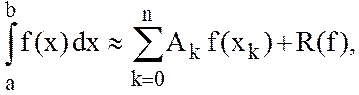                                 (11.2)

где  коэффициенты  A_k называют  весами, точки  x₀, x₁, x₂, … , x_k,, …  –  узлами  квадратурной  формулы. R(f) –методическая погрешность квадратурной  формулы  или  остаточный  член.

          Принцип построения  классических квадратурных  формул: данная подынтегральная функция  на интервале  заменяется интерполирующей  функцией  простого вида (например, интерполяционным многочленом), от которой легко находится интеграл. Для повышения точности  вычисления  интеграла  исходный отрезок  разделяют на  n частей с шагом 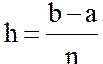. Тогда на каждом из полученных интервалов  строится свой  интерполяционный  многочлен  и искомый  интеграл 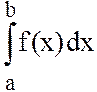 вычисляется как сумма  n частичных интегралов с помощью простейших  квадратурных  формул