Математическое моделирование систем и процессов. Часть 4: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 3

          Пусть требуется вычислить определенный интеграл 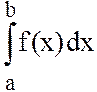.  Если известно, что данная подынтегральная функция f(x) на интервале интегрирования  не превышает некоторого значения С, то кривая  располагается внутри прямоугольника с основанием (b-a) и  высотой С (рис. 11.6).

          Моделируют процесс случайного попадания точек в обозначенный  прямоугольник. Для этого генерируют N пар случайных чисел  и  равномерно распределенных на интервалах  и  соответственно. Каждая пара   представляет собой координаты текущей точки. Таким образом получают N точек, равномерно рассеянных  внутри  прямоугольника.

          Тогда приближенное значение интеграла (оценка интеграла) может быть вычислено по формуле

                                        (11.16)

где   − количество точек, попавших  под кривую  N − общее количество точек (число испытаний, объем выборки); − площадь прямоугольника.

          Выражение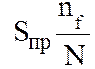 тем  точнее определяет  значение интеграла 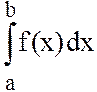, чем  больше объем  выборки  N (общее количество точек), то есть 

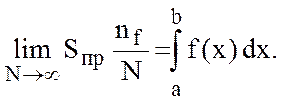                                    (11.17)

          Наиболее эффективно метод Монте-Карло применяется для оценки многомерных (кратных) интегралов. В отличие от других методов численного интегрирования  трудоемкость метода  Монте-Карло (объем  вычислений) слабо зависит от размерности решаемой задачи.

11.4. Информация  к  выполнению  задания  1

Вычисление значения определенного интеграла в заданиях 1.б, 1.в, 1.г реализовать программно с помощью встроенных средств программирования MathCad.

          В качестве примера приводится программа, реализующая в среде MathCAD вычисление определенного интеграла от функции   методом левых  прямоугольников:

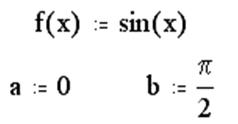
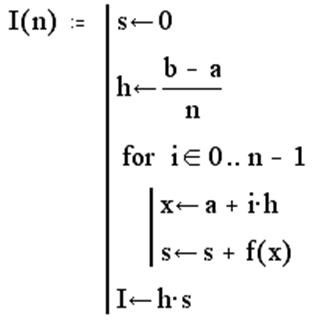
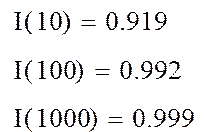
11.5. Информация  к  выполнению  задания  2

          В качестве примера рассмотрим процедуру оценивания методической погрешности  метода трапеций (см. формулу (11.13)) при числе разбиений интервала интегрирования  n = 1000.

      Пример выполнения задания 2

          1. Задание  исходных  данных:

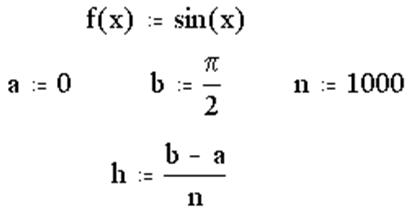
          2. Задание переменной  x  как  ранжированной  для построения графика второй производной подынтегральной функции на интервале интегрирования :

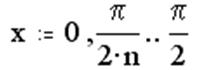
          3. Построение графика второй производной подынтегральной функции на заданном интервале интегрирования :

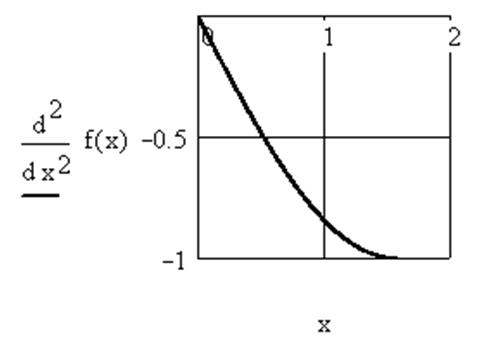
          4. Определение (визуально) по графику величины 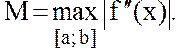 В данном случае  M = 1.

          5. Подстановка значения M в формулу (11.13) и получение оценки  методической  погрешности  метода  трапеций  R:

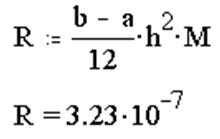
11.6. Информация  к  выполнению  задания  3

          Вычисление определенного интеграла методом Монте-Карло (методом статистических испытаний) предполагает  моделирование процесса случайного попадания точек в  прямоугольник с основанием (b-a) и  высотой С.  Для этого используется встроенная функция runif(N,m1,m2), которая генерирует последовательность из N независимых случайных чисел, имеющих равномерное распределение на интервале . 

          Переменная  nf − количество точек, попавших под кривую  из общего количества точек  N, равномерно рассеянных  внутри  прямоугольника.  

          Векторы X и Y формируются с помощью встроенной функции runif(N,m1,m2). Элементами векторов X и Y являются соответственно координаты  X_i и Y_i точек, попадающих внутрь прямоугольника с основанием (b-a) и  высотой С. Таким образом генерируемые значения координат X_i и Y_i должны удовлетворять условиям    и  .

          Пример выполнения задания 3

          1. Формирование  вектора  X:

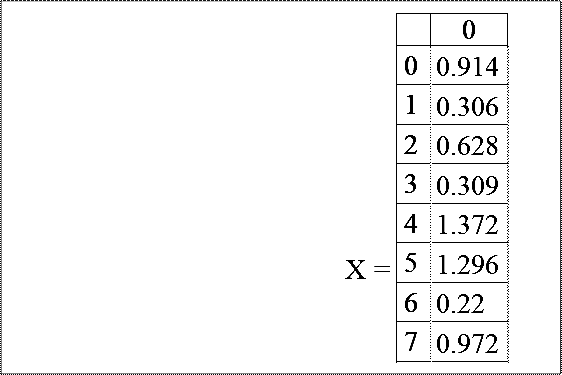
          2. Задание  верхней  границы  интервала :

          3. Формирование  вектора  Y:

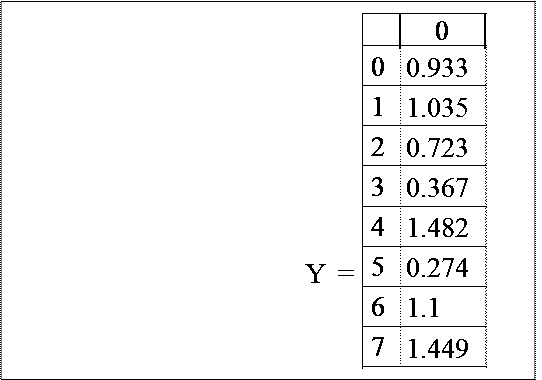
4. Вычисление  nf − количества точек, попавших  под  кривую   

     

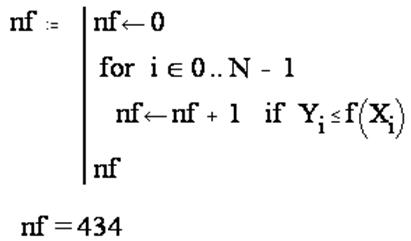
5. Вычисление площади прямоугольника с основанием (b-a) и  высотой С:

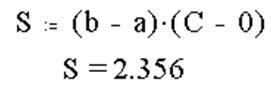
            6. Вычисление значения определенного интеграла:

                                                                       

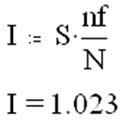
11.7. Информация  к  выполнению  задания  4

Встроенная функция  cspline(X,Y) вычисляет вектор вторых производных подынтегральной функции , используя приближение сплайн-функции  в узлах  кубическим  полиномом.

Встроенная функция interp(Pr,X,Y,x) вычисляет значение подынтегральной функции  в произвольной точке x с помощью интерполяции сплайн-функцией.

Пример выполнения задания 4

Пусть подынтегральная функция  задана таблицей значений y_i, определенных  в узлах  x_i:

x	0,2	0,4	0,6	0,8	1,0	1,2	1,4	1,6	1,8
y	3,5	9,0	4,1	4,8	7,3	15,5	19,7	10,0	11,9

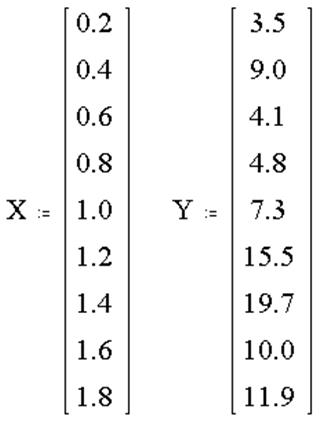
1. Задание вектора значений узлов X и вектора значений подынтегральной  функции Y:

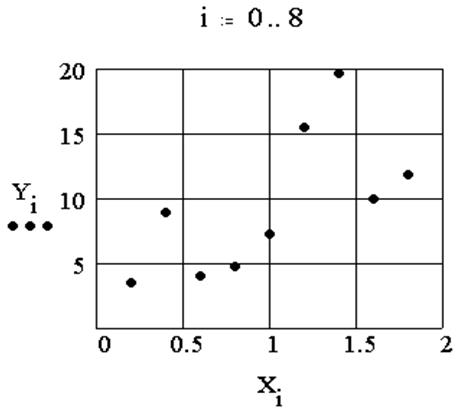
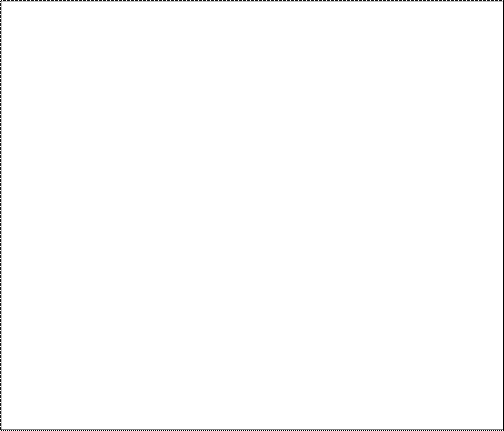2. Отображение на графике подынтегральной  функции  :

3. Вычисление определенного интеграла методом левых прямоуголь-ников:

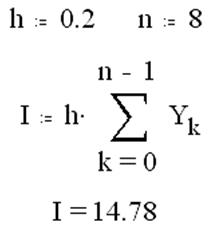
4. Вычисление определенного интеграла  методом  трапеций:

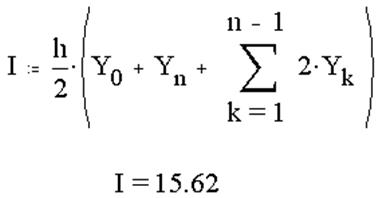
5. Вычисление определенного интеграла  методом  Симпсона:

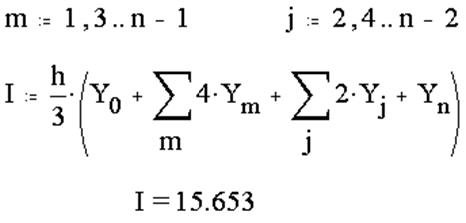
6. На  основе сплайн-интерполяции подынтегральной  функции  c последующим  применением  оператора  интегрирования:

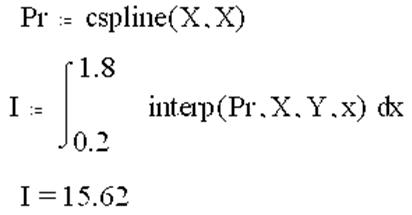
11.8. Задания

          1. Вычислить значение определенного интеграла детерминированными численными методами для подынтегральной функция f(x) заданной аналитически (табл. 11.1):

а) с помощью оператора  интегрирования;

б) методом  средних  прямоугольников (для n = 10,100,1000);

в) методом  трапеций (для n = 10,100,1000);

г) методом  Симпсона (для n = 10,100,1000).

          2) Оценить методические погрешности методов средних прямоугольников и Симпсона  при  n = 10,1000.

          3) Вычислить значение определенного интеграла методом Монте-Карло (методом статистических испытаний).

          4) Вычислить значение определенного интеграла для подынтегральной функции  f(x) заданной таблично (табл. 11.2):

а) методом левых прямоугольников;

б) методом  трапеций;

в) методом  Симпсона;

г) на основе сплайн-интерполяции подынтегральной функции  c последующим применением оператора интегрирования.

Таблица 11.1

Исходные данные для численного интегрирования функции,

заданной  аналитически

Вариант	Определенный интеграл	Вариант	Определенный интеграл
1	2	4	3
1		9
2		10

Окончание табл. 11.1