Основы и принципы работы в VBA. Часть 1: Методические указания к выполнению лабораторных работ, страница 5

2.3. Дополнительное задание

Составить алгоритм и программу решения системы двух уравнений методом подстановки при произвольных коэффициентах  a,  b,  u,  c,  d,  v:

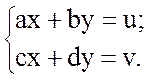
Ввод коэффициентов произвести с помощью  оператора InputBox, вывод результатов – на рабочий лист Excel.

Выполнить проверку полученных результатов.

Лабораторная работа 3

ПРОГРАММИРОВАНИЕ  РАЗВЕТВЛЯЮЩИХСЯ  ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ.  ПРОСТОЕ  ВЕТВЛЕНИЕ

Цель работы: изучение особенностей разработки алгоритмов с разветвляющейся структурой и их реализации с помощью операторов условного перехода.

3.1. Краткие теоретические сведения

Для  записи разветвляющихся алгоритмов используется оператор If, он имеет две формы записи:

          однострочную:

IfусловиеThen[оператор1] [Elseоператор2];

          многострочную:

Ifусловие-1 Then
                     [ оператор1]

                    [ElseIfусловие-2 Then
                                                            [оператор2] ...

                          [Else
                                   [оператор3]]

EndIf

В условии записывается логическое выражение, в котором используются операции сравнения. Для создания сложных условий применяются логические операции and(и) и  or(или).

Пример. Вычислить значение функции 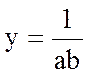 при любых значениях a и b. На первый взгляд решение этой задачи можно описать алгоритмом  линейной структуры, однако при условии ab = 0 задача не может быть решена, так как деление на ноль невозможно. Для корректного решения задачи необходимо предусмотреть вывод сообщения, если вычисление y невозможно. В этом случае вычислительный процесс можно описать следующим образом: вычислить y, если ab ≠ 0,  или вывести сообщение, если  ab = 0.

В ГСА решения этой задачи (рис. 3.1) используется блок проверки условия, имеющий один вход и два выхода по выполнению проверяемого условия – «Да» и «Нет» (в данном примере – это блок 2, в котором проверяется условие ab = 0). В зависимости от результата проверки условия возможны два пути продолжения решения задачи. Каждый из путей называется       ветвью, а алгоритм – разветвляющимся.

Как и во всех разветвляющихся алгоритмах в данном примере нарушается ес-тественный порядок следования блоков. Так, за блоком 2 может выполняться блок 3, образуя ветвь 1, или блок 5, образуя ветвь 2; за блоком 4 всегда выполняется блок 6.

Любое изменение естественной (линейной) последовательности выполнения блоков называется переходом. Переходы бывают двух типов: условные и безусловные. Условный переход реализуются с помощью оператора условия (условного оператора).

Для рассматриваемого примера оператор условия для блочной структуры можно записать в виде:

Программный код

Sub V ( )

Dim a As Single,  b As Single, y As Single

a=Val(InputBox("a ="))

b=Val(InputBox("b ="))

If  a*b=0  Then

MsgBox ("ab=0")

Else  y=1/ (a*b)

MsgBox ("y="& y)

End If

End Sub

Если условие выполняется, т. е. ab= 0, то в окне вывода на экран монитора оператором MsgBox выводится сообщение "ab=0", в противном случае, когда    ab≠ 0, вычисляется значение y по формуле y=1/(a*b), котороевыводится в стандартном окне вывода.

Вариант программы с  линейной формой записи оператора:

Программный код

Option  Explicit

Sub V ( )

Dim a As Single,  b As Single, y As Single

a=Val(InputBox("a="))

b=Val(InputBox("b="))

IF a*b=0 Then MsgBox("ab=0")  Else  y=1/(a*b):  MsgBox ("y="&  y) 

End Sub

3.2. Индивидуальные задания

3.2.1. Примеры проверки числа на кратность

 Разработать программу ввода и вывода натурального целого числа а (а ≥ 0), проверяющую кратность этого числа:

1)  if a mod b = 0 then MsgBox ("да") else  MsgBox ("нет") ;

2)  if a/3 = fix (a/3) then MsgBox ("да") else MsgBox ("нет");

3)  if a/3 = int (a/3) then MsgBox ("да") else MsgBox ("нет");

4)  if a/3 = cint (a/3) then MsgBox ("да") else MsgBox ("нет");

5)  if a/3 = a\3 then MsgBox ("да") else MsgBox ("нет").

3.2.2. Использование линейной формы записи операторов

условной передачи управления

Составить программу разветвляющихся вычислительных процессов (ввод и вывод выполнить с использованием функций соответственно InputBoxи MsgBox) линейной формы записи оператора условного перехода.

1) Выполнить расчет значения переменных C и В по формулам   при  a = 9,5; x = 7. Вывести полученные значения С и В в диалоговое окно оператора MsgBox в порядке их возрастания.

2) Даны два числа – К и L. Вывести на печать то из чисел, для которого получается больший целый остаток от его деления на четыре.

3) Даны два числа – А и D. Определить и  вывести на печать целый остаток от деления большего из чисел на меньшее.

4) Даны два вещественных числа – В и С. Вывести на печать заданные числа в порядке убывания их целых частей.

5) Даны два числа – R и N. Вывести эти числа на печать в порядке убывания их модулей.

6) Даны два числа – K и N. Если разность этих чисел является четным числом, то вывести на экран их сумму, в противном случае – их произведение.

7) Даны два числа – V и W. Вывести на печать сумму модулей этих чисел, если произведение чисел кратно трем, в противном случае – разность этих
чисел.

8) Даны два числа – С и W . Определить, является ли первое число кратным второму.

9) Даны два вещественных числа – Р и С. Вывести  на печать сумму этих чисел, если целая часть их разности не превышает 10, в противном случае – произведение этих чисел.

10) Даны два числа – С и К. Вывести на печать разность этих чисел, если целая часть их отношения равна нулю, в противном случае – сумму этих чисел.

11) Даны два вещественных числа – J и M. Определить, является ли целая часть суммы заданных чисел кратна пяти.

12) Из двух заданных вещественных чисел (A и N) вывести на печать то, у которого дробная часть меньше.

13) Даны два вещественных  числа – Р и Q. Вывести эти числа на печать в порядке убывания их дробных частей.

14) Даны два числа – К и В. Вывести  на печать сумму этих чисел, если К больше В, в противном случае – их разность.

15) Даны два числа – Н и У. Если сумма заданных чисел кратна трем, то вывести на печать их произведение, в противном случае – среднеарифмети-ческое этих чисел.