Другие предметы \ Математическое моделирование систем и процессов

Математическое моделирование систем и процессов. Часть 1: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 7

Математические модели в форме дифференциальных уравнений в частных производных, описывающие процессы различной физической природы, с помощью известных приближённых методов сводятся к решению СЛАУ.

Таким образом, решение СЛАУ приобретает особое значение в процессе математического моделирования систем и процессов. В связи с этим необходимо уделить серьёзное внимание методам решения математических моделей этого класса.

В данной лабораторной работе рассмотрим две группы методов решения СЛАУ  –  прямые (точные) и  итерационные (приближенные).

4.2.     Информация к выполнения задания 1

Для реализации метода Гаусса в среде MathCAD требуется ввести понятие расширенной матрицы системы. Для системы (1) расширенная матрица имеет вид: 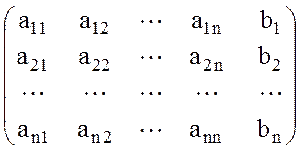.                                                           (3)

Прямой ход метода Гаусса приводит расширенную матрицу системы к ступенчатому  виду:

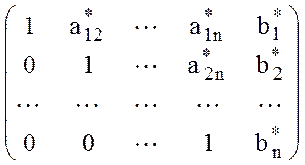                               .                                   (4)

Обратный ход преобразует матрицу (4) к  виду

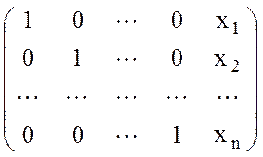                               ,                                      (5)

где последний столбец содержит  решение системы (1).

          Для реализации метода Гаусса рекомендуется использовать следующие встроенные  функции  MathCAD:

augment(A,B) − формирует расширенную матрицу, путём добавления к матрице коэффициентов системы А столбца свободных членов B;

rref(AR) − приводит расширенную матрицу системы (3) к виду (5) , т. е.  rref(AR) реализует прямой и обратный ходы метода Гаусса;

submatrix(AS,iн,iк,jн,jк) − выделяет фрагмент матрицы AS (iн и iк − номера соответственно начальной и конечной строк выделяемого фрагмента, jн и jк − номера начального и  конечного столбцов выделяемого фрагмента).

Пример выполнения задания 1

Дана  СЛАУ:

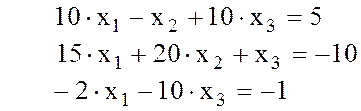
                                     (6)

Фрагмент рабочего документа MathCAD

1. Задание матрицы коэффициентов системы  А  и  вектора свободных членов B:

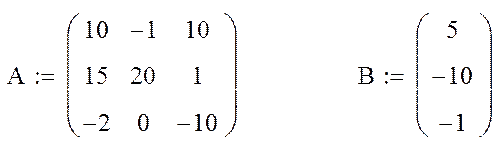
2. Формирование  расширенной  матрицы системы  AR

3. Выполнение прямого и обратного ходов метода Гаусса и приведение расширенной матрицы системы AR к виду (5)

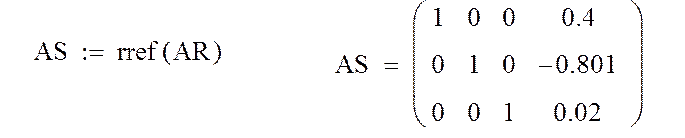
4. Выделение из матрицы AS последнего столбца, представляющего собой  решение  заданной  системы  X

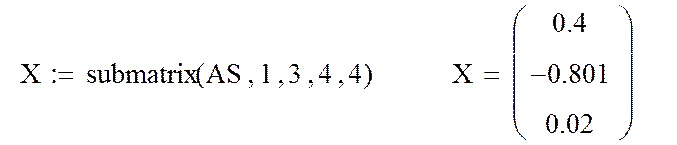
5. Проверка правильности решения

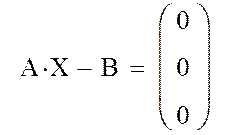
4.3.     Информация  к выполнения  задания 2

Для реализации метода LU- разложения рекомендуется использовать следующие встроенные функции MathCAD:

lu(A) − осуществляет LU-разложение матрицы A, а именно формирует составную матрицу Q:

для    A =;      Q =;

submatrix (Q, … , … , … , …) − выделяет фрагмент матрицы Q.

Пример выполнения задания 2. Решение СЛАУ (6).

Фрагмент рабочего документа MathCAD

1. LU-разложение матрицы коэффициентов A и формирование составной матрицы Q:

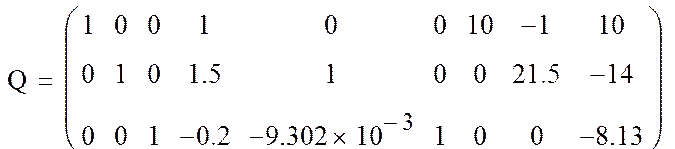
2. Выделение нижней треугольной матрицы L из составной матрицы Q:

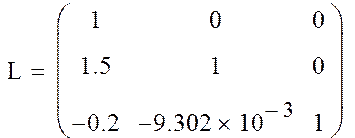
3. Выделение верхней треугольной матрицы U из составной матрицы Q:


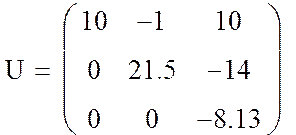
4. Определение вектора вспомогательных переменных G:

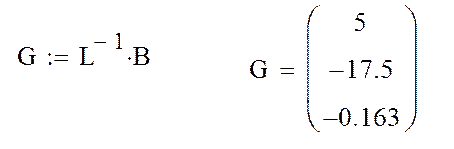
5. Определение вектора решения системы  X

4.4.     Информация  к выполнения  задания 3  

Обозначение:   det A= – определитель матрицы A.

Пример выполнения задания 3. Решение СЛАУ (6).

Фрагмент рабочего документа MathCAD

1. Проверка условия невырожденности матрицы A

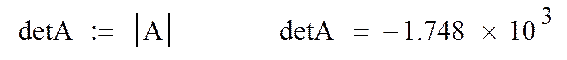
2. Определение решения системы  X

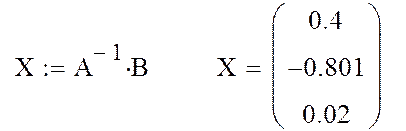
4.5.     Информация  к выполнения  задания 4  

          Метод итерации относится к разряду приближённых.

          Рекомендуется использовать специальный вычислительный блок MathCAD:

Given

··················· = ····

··················· = ····

··················· = ····

Find (x1, x2, … , xn)

Знак логического оператора «=» можно ввести в  документ с панели инструментов Математика =>  палитры  Операторы  или с помощью сочетания клавиш  Ctrl  +  =.

В качестве начальных (нулевых) приближений для искомых неизвестных:

рекомендуется принимать соответствующие значения свободных членов

Пример выполнения задания 4.  Решение СЛАУ (6).

Фрагмент рабочего документа MathCAD

1. Задание начальных (нулевых) приближений для искомых неизвестных:

2. Нахождение решения системы (6)

10·x1–x2+10·x3=5

15·x1+20·x2+ x3=–10

–2·x1–10·x3=–1

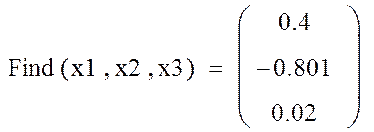
4.6.  Информация  к выполнения  задания  5

Пример выполнения задания 5.  Решение СЛАУ (6).

Фрагмент рабочего документа MathCAD

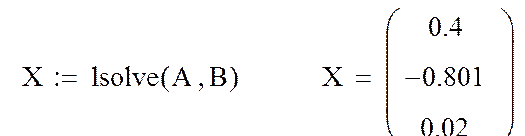
4.7. Задания

1. Решить заданную СЛАУ ( из табл. 4.1.) методом Гаусса.

2. Решить заданную СЛАУ методом  LU- разложения.

3. Решить заданную СЛАУ матричным методом.

4. Решить заданную СЛАУ методом  итерации.

5. Решить заданную СЛАУ c помощью встроенной функции MathCAD  lsolve (…)

Таблица 4.1

вариант

СЛАУ

Решение

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

Библиографический  список

1. Дьяконов В. П. Энциклопедия Mathcad 2001i  и  Mathcad 11 /  В.П. Дьяконов М.: СОЛОН-Пресс, 2004. 832 с.

2. Ивановский Р.И. Компьютерные технологии  в науке и образовании. Практика применения систем MathCAD Pro: Учебное  пособие / Р.И. Ивановский. М.: Высшая школа, 2003. 431 с.

3. Голубева Н.В. Основы математического моделирования систем и процессов: Учебное пособие/ Н.В. Голубева. Омск, 2006. 96 с.

Скачать файл