Математическое моделирование систем и процессов. Часть 1: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 4

k := 0 .. 100

2.3. Вывод таблицы значений функции

          Для того чтобы представить функцию в виде таблицы значений, в качестве её аргумента используют ранжированную переменную. (Поэтому часто используется термин «дискретный аргумент»)

Пример  2.1.  Получить таблицу  значений  функции  

для  b = 1,75;   с шагом  ∆x = 0,3.

Решение:

1) присвоить заданное значение переменной b:

b := 1.75

2) задать аргумент  x  как ранжированную переменную:

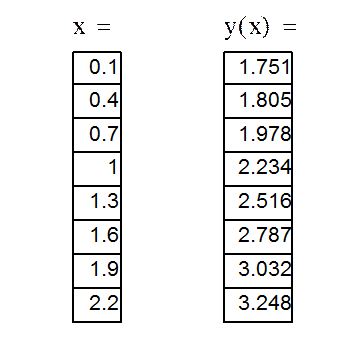
x := 0.1,0.4 .. 2.2

3) ввести выражение для функции y:

− после имени функции в скобках обязательно указать тот аргумент, который задан как ранжированная переменная (в данном примере это  x):

− в маркер ввода ввести шаблон встроенной функции  (это arctg на языке MathCAD), с помощью одного из инструментов Вставка функции

− в маркер ввода  ввести аргумент x, затем оставшуюся часть выражения:

;

4) в следующей строке ввести с клавиатуры x=. При этом сразу появится таблица значений аргумента x. Затем в этой же строке ввести y(x)= , появится таблица значений функции  y:

2.4. Построение графиков

Пример  2.2.  Построить график функции   при  a=0,55;  с шагом  ∆x = 0,25.

Решение:

1) присвоить заданное значение переменной  a:  

a := 0.55

2) задать аргумент  x  как  ранжированную переменную

x := 0.5,0.75 .. 8

3) ввести функцию f(x) (использовать встроенную функцию ):

4) вставить шаблон двумерного декартова графика. При этом появляется пустая область графика с двумя маркерами ввода;

5) в маркер ввода под осью абсцисс в центре ввести имя аргумента x; в маркер ввода левее оси ординат ввести f(x); щёлкнуть вне области графика. Результат представлен на  рис.2.1;

6) увеличить область графика. Для этого выделить ее штриховой рамкой. Навести указатель мыши на нижний правый угол рамки, добившись, чтобы он принял форму . При нажатой ЛКМ протягивать указатель вниз и вправо.

2.5. Форматирование  графика

Форматирование графика подразумевает изменение внешнего вида, оформления элементов графической области (осей, координатной сетки, кривой, отображающей зависимость y(x), шкалы, маркеров и т.д.). Для форматирования графика (рис. 2.1) следует:

1) выделить область графика щелчком (появляется синяя рамка);

2) с помощью одного из инструментов: меню Декартов график => Формат  или двойной щелчок по области графика вызвать диалоговое окно Форматирование текущего X-Y графика;

3) на вкладке X-Y Оси щелчком мыши установить параметры: наличие линий сетки и число интервалов сетки на осях; выделение координатной оси абсцисс (Репер); наличие цифровых данных по осям и т. д.;

4) на вкладке Графики установить параметры: тип графика, стиль, цвет, толщина линии, наличие маркеров;

5) на вкладке Надписи ввести заголовок к графику и надписи к осям.

Пример 2.3.  Построить в той же графической области (созданной в примере 2.2) график второй функции  g(x)=x³cos3x

Решение:

1) охватить синим курсором-рамкой ранее введенную функцию f(x) слева от оси ординат (рис.2.2):

2) нажать клавишу . При этом ниже появляется маркер ввода.

3) в маркер ввода ввести  g(x) и щёлкнуть вне области графика. Результат представлен на рис.2.3.

2.6. Символьные  преобразования

Система MathCAD включает в свой состав несколько интегрированных между собой компонентов. В их числе – мощный вычислительный процессор, предназначенный для выполнения численных расчетов по введенным формулам на основе встроенных численных методов, а также символьный процессор, являющийся по своей сути системой искусственного интеллекта. Символьный процессор предоставляет широкие возможности для символьных вычислений, позволяющих решать многие задачи аналитически.

Если результатом численного расчета  является число или набор чисел, то в результате символьных  вычислений  получаются  выражения.

Для того, чтобы задействовать для решения задачи символьный процессор  используют  следующие  инструменты:

1)команды  меню  Символика

2)оператор символьного вывода =>  кнопка  с палитры Операторы

Пример 2.4.  Упростить  выражение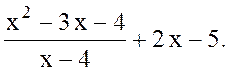  

Решение:

1)ввести  исходное  выражение и охватить его  курсором – рамкой

2) применить  команду  меню  Символика => Упростить

В результате в следующей строке появится результат упрощения.

Фрагмент рабочего документа MathCAD:

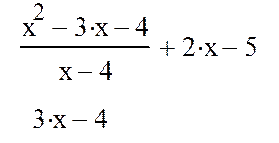
Аналогичным образом выполняются символьные команды разложения выражений на простейшие множители, рациональных дробей на простые дроби, команда «развернуть», реализующая раскрытие скобок, перемножение и приведение подобных членов и др.

Примечание.  Если символьная команда выполняется относительно какой-либо переменной (разложение в ряд, решение уравнения, интегрирование, дифференцирование), то следует выделить эту переменную (можно охватить ее курсором – рамкой или просто установить на нее курсор ввода данных).

Пример 2.5.  Интегрировать  выражение 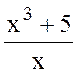   по  переменной  x.

Способ  1−с помощью оператора  символьного вывода ®:

1) с палитры Операторы математического анализа  ввести оператор интегрирования:

2) в соответствующие маркеры ввода ввести подынтегральное выражение и переменную интегрирования;

3) охватить все выражение курсором – рамкой, затем ввести оператор символьного вывода ® с палитры  Операторы

4) выполнить щелчок  вне области формулы, после чего справа  появится результат символьного  вычисления:

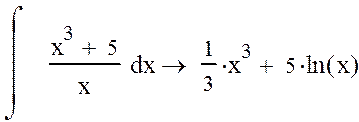
Способ 2−с помощью меню  Символика:

1) ввести  подынтегральное  выражение;

2) установить курсор на переменной интегрирования  x

3) применить команду меню  Символика=> Интегрировать  по переменной. При этом в следующей  строке появляется  результат: