Математическое моделирование систем и процессов. Часть 1: Методические указания к выполнению лабораторных работ и самостоятельной работы, страница 6

          Для выделения из матрицы строки следует применить оператор < > к транспонированной матрице. Например, выделим третью строку из матрицы  V:

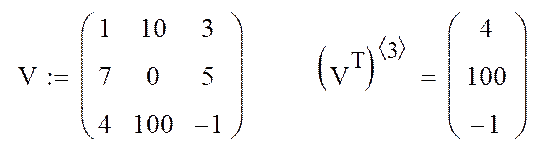
3.2. Средства  MathCAD  для  реализации  матричных  вычислений

          Система MathCAD реализует матричные вычисления с помощью мат-ричных операторов  и  встроенных функций.

          Для  ввода матричных операторов используют инструменты:

1.Ввод  с  клавиатуры. Реализуются операции: сложение, вычитание, перемножение матриц, умножение на скаляр, определение обратной матрицы.

Пример 3.2.  Выполнить матричные операции путем ввода с клавиатуры

Фрагмент рабочего документа MathCAD.

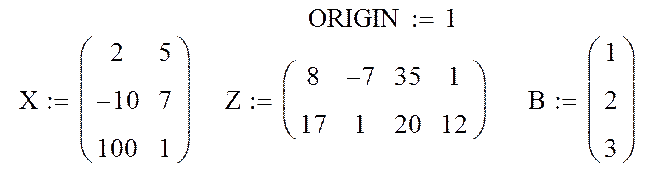
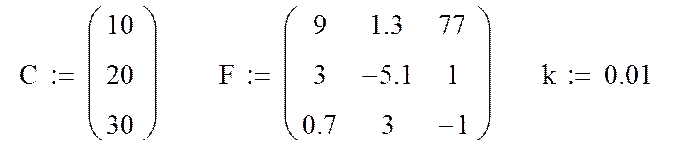
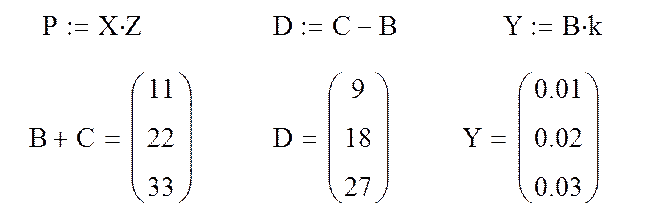
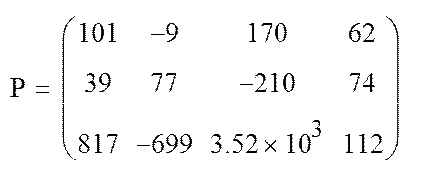
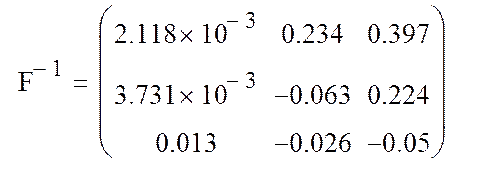
2. Ввод с панели  инструментов  Математика=>  палитры Векторные и матричные операции  с помощью кнопок транспонирование матрицы ; вычисление определителя матрицы ; вычисление суммы элементов вектора ; вычисление скалярного произведения векторов ; вычисление векторного произведения векторов  и т.д.

Пример 3.3.  Реализовать матричные операции с помощью панели  инструментов  Математика.

Фрагмент рабочего  документа  MathCAD.

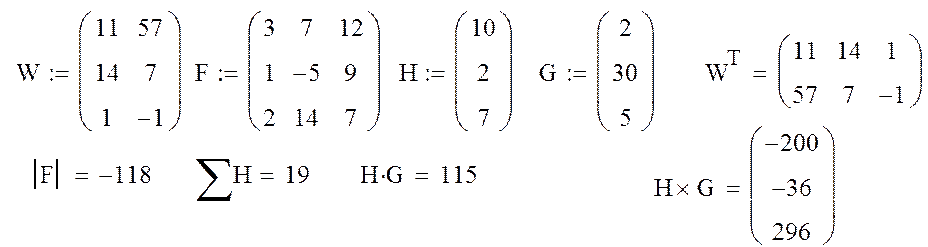
3.3. Встроенные функции

          Встроенные функции для матричных вычислений можно условно разделить на несколько групп:

функции для создания матриц (единичных, диагональных, функциональных);

функции для слияния матриц или выделения фрагмента матрицы;

функции для определения числовых характеристик матриц (следа, ранга, норм, количества элементов, минимальных, максимальных элементов и т.д.);

функции, реализующие численные методы решения задач линейной алгебры.

          Рассмотрим примеры применения следующих встроенных функций MathCAD: DIAG(v) – создание диагональной матрицы, на главной диагонали кото-рой размещаются элементы вектора v; stack(M1,M2) – объединение двух мат-риц M1 и M2 в одну, путём подсоединения М2 к М1 снизу (матрицы M1 и M2 должны иметь одинаковое количество столбцов); max(M) – определение мак-симального элемента в матрице М (векторе); min(M)– определение минимального элемента в матрице М (векторе); tr(M) – вычисление следа квад-ратной матрицы М (след матрицы равен сумме её диагональных элементов); sort(v) – сортировка элементов вектора v в порядке возрастания; csort(M,n) – перестановка строк матрицы М таким образом, чтобы элементы  n-го столбца оказались упорядоченными по возрастанию; mean(M) – вычисление среднего арифметического значения элементов матрицы (вектора) М.

Пример 3.4.   Применение встроенных функций  MathCAD

Фрагмент рабочего документа MathCAD.

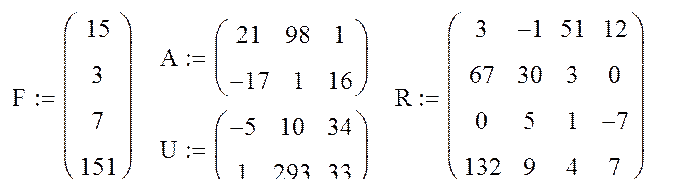
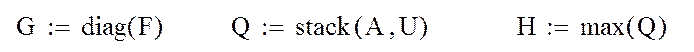
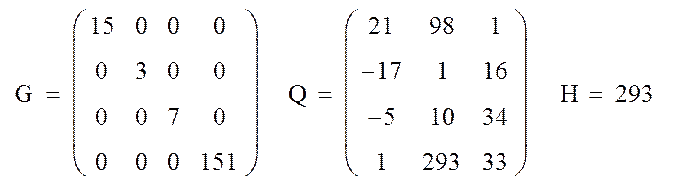
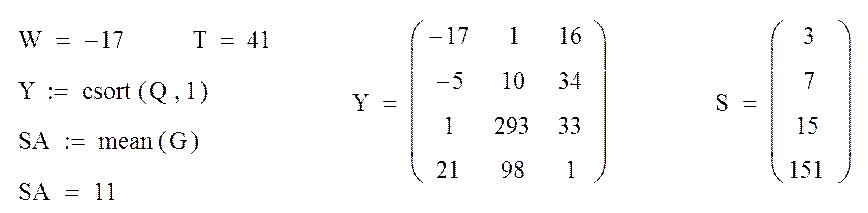
3.4. Задания

1. Создать текстовую область, в которую ввести ФИО, группу, № и название лабораторной работы.

2. Ознакомиться с инструментами ввода матриц в документ MathCAD.

3. Выполнить примеры  3.1, 3.2, 3.3, 3.4.

4. Определить произведение матриц А и В (матрицу Авзять из табл. 3.1., матрицу  B задать  произвольно).

5. ОпределитьА^Т, В^Т, матрицу  В умножить  на скаляр  k = 0,001.

6. Ввести  две произвольные матрицы Q и R одинакового размера. Произвести  сложение Q+R и  вычитание Q−R.

7. Ввести  две  произвольные  матрицы  Z  и  W. Объединить матрицы  Z  и  W  в одну с помощью  встроенной  функции  stack(… , …).

8. На произвольных матрицах T и J продемонстрировать действие встроенной функции, формирующей новую матрицу путем объединения двух заданных  матриц  T  и  J  «бок о бок».

9. Ввести матрицу Н (из табл. 3.1.). Вычислить определитель  и получить обратную матрицу .

10. Ввести вектор V (из табл. 3.1.). Определить сумму элементов вектора, максимальный и минимальный элементы в нём, транспонировать его. Упорядочить его элементы по возрастанию. Создать на основе вектора Vдиагональную матрицу.

11. Произвести перестановку строк матрицы Нтаким образом, чтобы элементы 3-го столбца оказались упорядоченными по возрастанию; определить среднее арифметическое значение элементов матрицы  Н.

Таблица 3.1.

Вариант	H	А	V
1
2
3
4
5
6
7

Продолжение табл. 3.1.

8
9
10
11
12
13
14

Окончание табл. 3.1.

15
16
17

Лабораторная  работа  4

МАТЕМАТИЧЕСКИЕ  МОДЕЛИ  В  ФОРМЕ  СИСТЕМ  ЛИНЕЙНЫХ

 АЛГЕБРАИЧЕСКИХ  УРАВНЕНИЙ  И  МЕТОДЫ  ИХ  РЕШЕНИЯ 

4.1. Постановка  задачи

Некоторые физические системы могут быть адекватно описаны математической моделью в виде системы линейных алгебраических уравнений (СЛАУ)

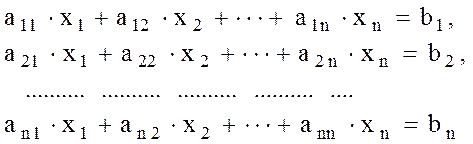                         (1)

которая  может быть представлена  в  векторно - матричной форме:

,                                                      (2)

где  – вектор свободных членов,  – вектор неизвестных,  A – матрица коэффициентов системы, размером  .         

При исследовании многих сложных систем и процессов на промежуточных этапах формирования их математической модели, часто возникает необходимость решения СЛАУ. Например, при аппроксимации экспериментальных данных функцией определённого класса.