Магнитное поле: Краткая теория и образцы решений некоторых задач, страница 4

                                         А = I  (Ф₂ – Ф₁),                                          (3.3.9)

где Ф₁ и Ф₂ – магнитные потоки сквозь рамку в положениях 1 и 2.

    Работа сил Ампера  по перемещению проводника с током в магнитном поле :

                                                          А = I DФ,                                          (3.3.10)

где Ф - магнитный  поток через площадь, которую описывает проводник при своем движении.

    Пример. Определить работу, совершаемую полем при повороте контура из положения р_m çç  В  в положение устойчивого равновесия, а также работу, которую необходимо совершить для удаления контура, находящегося в положении устойчивого равновесия, в область, где поле равно нулю. Считать значения магнитного момента р_m и индукции поля  В известными.

     Решение. В первой половине вопроса речь идет о работе, совершаемой силами Ампера и определяемой по формуле (3.3.9) :

                             А = I (BS cos 0 ⁰ – BS cos 90 ⁰ ) = p_m B.

Во второй половине речь идет о работе внешних сил против сил Ампера. Поэтому она имеет знак “минус”. Первое положение здесь – это положение устойчивого равновесия, магнитный поток максимален, а во втором положении магнитный поток равен нулю. Тогда :

                             А = - I (Ф₂ – Ф₁) = -I (0 – ВS) = р_mВ.

4. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ.

    Согласно закону электромагнитной индукции, при изменении магнитного потока Ф, пронизывающего контур, в последнем возникает ЭДС индукции ε _i, пропорциональная скорости изменения магнитного потока во времени :

                                            ε_i  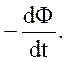=                                                        (3.4.1)

    Знак “минуc” в выражении (3.4.1) соответствует правилу Лоренца: индукционный ток  всегда направлен таким образом, чтобы противодействовать причине, его вызвавшей.

    Если контур содержит N витков и каждый виток сцеплен с переменным магнитным потоком Ф, то

                             ε _{i =   ,}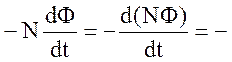

здесь N · Ф = Ψ – полный магнитный поток или потокосцепление.

    Изменение магнитного потока может быть обусловлено равными причинами, связанными с изменением : магнитной индукции во времени; формы контура (площади, охватываемой им); угла между нормалью к плоскости и вектором В (например, при вращении рамки в магнитном поле); площади, описываемой проводником, пересекающим силовые линии поля и т.д. Поэтому при решении задач на эту тему надо, прежде всего, установить причину изменения магнитного потока.

    Пример. Найти заряд, протекающий по замкнутому витку с сопротивлением R, при удалении его из магнитного поля. Магнитный поток сквозь виток        равен Ф.

     Решение.Причина изменения  магнитного потока – исчезновение поля, магнитный поток сначала был равен Ф, затем снизился до нуля. Так как проводник замкнутый, по нему течет индукционный ток I. Тогда заряд, прошедший по витку, q  = I dt^΄. По закону Ома I = ε _i / R, а ЭДС индукции ε _i = - dФ / dt. Тогда :

                             q  =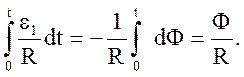         

Ответ : q = Ф / R.

    Пример. Прямолинейный проводник длиной l движется в однородном магнитном поле так, что его скорость v составляет угол β с направлением силовых линий. Найти ЭДС индукции, возникающей на концах проводника. Магнитная индукция поля В считается известной.

 

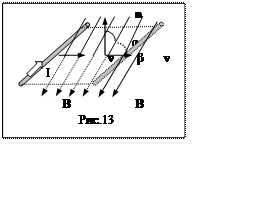    Решение. Причина изменения магнитного потока – изменение площади, пересекаемой проводником при его движении. Поэтому скорость изменения магнитного потока во времени

dФ/dt = B(dS/dt) cosα.

dS/dt – площадь, пересекаемая проводником в единицу времени, равная ldx/dt = lν, а угол α  дополняет угол β до 90 ⁰ (рис. 13). Тогда

ε_i  = - B l ν sin β.

    Ответ:  ε _i = - B l ν sin β.

Пример.   Рамка площадью 100 см² вращается в магнитном поле с индукцией 0,2 Тл так, что ось вращения расположена перпендикулярно силовым линиям магнитного поля. Рамка делает 5 оборотов в секунду. Найти значение ЭДС индукции в момент времени t = 2с и максимальную ЭДС индукции в рамке. В начальный момент времени плоскость рамки располагалась перпендикулярно силовым линиям поля.

    Решение. Причина изменения магнитного потока здесь – изменение угла между нормалью к рамке и магнитной индукцией, причем угловая скорость вращения ω = 2πn (n – число оборотов в единицу времени.). Согласно основному закону электромагнитной индукции :

                     

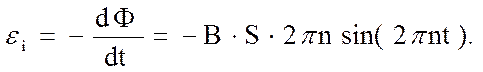
Подставив числовые данные, получим в момент t = 2 c

                   ε _i  = - 0,2 · 10 ^{– 2} · 2 · 3,14 · 5 · sin (2π · 5 · 2) = 0  

Максимальное значение ЭДС находим из условия, что  sin (2πn) =1:

ε _maх = 0, 2 · 10 ^{– 2} · 2 · 3,14 · 5 = 0, 0628 В.

    Ответ : В момент времени 2 с ЭДС индукции равна нулю.

               Максимальная ЭДС индукции 0, 0628 В.

    Если по контуру протекает изменяющийся во времени ток, то в контуре возникает ЭДС самоиндукции :

                                            ε _S  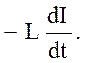 =                                                  (3.4.2)

где L – индуктивность контура, определяемая отношением потокосцепления к силе тока в контуре :

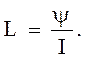                                                                                                           (3.4.2 ΄ )

В СИ индуктивность измеряется в Генри (Гн).

                                              

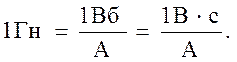
     Выведем формулу для индуктивности соленоида. При протекании тока по соленоиду длиной l в нем возбуждается магнитное поле, индукция которого на оси соленоида определяется формулой (3.2.4). Потокосцепление 

,

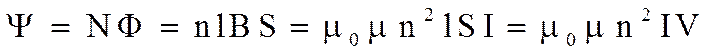где Ψ = BS – поток, пронизывающий каждый из витков; S – площадь поперечного сечения соленоида; N = nl – общее число витков. Следовательно, индуктивность соленоида равна

,

где  IS = V – объем соленоида. По этой формуле вычисляется индуктивность соленоида без сердечника  или немагнитным сердечником ( в том и другом случае μ = 1 ).

    Если соленоид содержит ферромагнитный сердечник, то надо сначала определить значение магнитной проницаемости  материала сердечника. Для этого надо знать ход кривой   B = f(H) (рис.14).