Магнитное поле: Краткая теория и образцы решений некоторых задач, страница 2

                                 В =  = .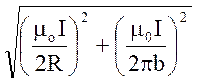

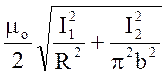Подставляя числовые данные задачи, получим:

                           В = 23,14 · 10^-7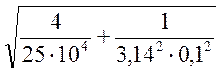 = 25мкТл.

Ответ: В = 25 мкТл.

2.  МАГНИТНЫЙ ПОТОК, ПОТОКОСЦЕПЛЕНИЕ.

ТЕОРЕМА ГАУССА И ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА В

    Поток магнитной индукции Ф_м через некоторую поверхность S 

                           Ф_м = ∫(В dS) =B dS cosα = ∫B_ndS ,                       (3.2.1)

                                   ^{S                           S                                         S}

где круглые скобки означают скалярное произведение векторов;  α – угол между нормалью n к площадке и направлением магнитной индукции В; В_n  - проекция магнитной индукции на нормаль; dS =  n·dS. В случае однородного магнитного поля и плоской поверхности S

                                                    Ф = BScosα.                                  (3.2.1)

Единица измерения магнитного потока в СИ – вебер (Вб), 1 Вб = 1 Тл ·1м².

    Пример. Виток радиусом 2 см расположен в однородном магнитном поле с индукцией В = 2 мТл так, что его плоскость составляет 30⁰ с силовыми линиями. Найти магнитный поток через виток.

    Решение. Используем формулу (3.2.1^΄), подставив в нее площадь круга. Угол α в данном случае равен 60⁰. А не 30⁰ (обратите внимание на распространенную ошибку), что видно из рис. 7. Посмотрите еще раз пояснение к формуле. Таким образом, магнитный поток

Ф = 2 · 10^-3Тл 3,14 · 4 · 10^-4 м = 2,5мкВб.

Ответ: Ф = 2,5 мкВб. 

    Так как линии вектора В всегда замкнуты, то число линий, выходящих из объема V, равно количеству линий, входящих в него. Поэтому поток вектора В через любую замкнутую поверхность равен нулю:

                                            Ф_в = 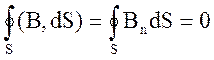                                  (3.2.2)

В этом состоит смысл теоремы Гаусса  для магнитного поля.

Если контур состоит из N витков, каждый из которых пронизывается магнитным потоком Ф, алгебраическая сумма потоков

                               Ψ = Ф₁ + Ф₂ + . . . =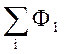.                                       (3.2.2΄)

Величина Ψ  называется потокосцеплением или полным магнитным потоком, измеряется так же, как и магнитный поток, в веберах.

     Теорема о циркуляции вектора магнитной индукции утверждает, что циркуляция вектора В вдоль замкнутого контура в отсутствие переменных электрических полей равна алгебраической сумме токов, охватываемых контуром:

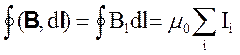                                                                                   ( 3.2.3)

Значение силы тока берут со знаком «плюс», если направление тока и направление обхода контура составляет правовинтовую систему, и со знаком « минус», если левовинтовую. Выбор направления обхода произволен. Если ток охватывает контур N раз, то это обстоятельство учитывают произведением NI.

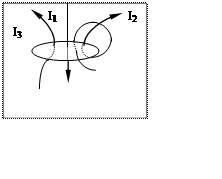
    Пример.  На рис.8 изображен произвольный контур, охватывающий несколько проводников с токами. Токи равны: I₁ = 1 A; I₂ = 2 A; I₃ = 1,5 A. Найти циркуляцию вектора магнитной индукции вдоль этого контура.

    Решение. Согласно формуле (3.2.3). циркуляция вектора В имеет  вид 

                       

Проведем операции с размерностями и покажем, что циркуляция измеряется в Тл·м:

                                        

 

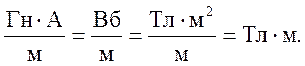
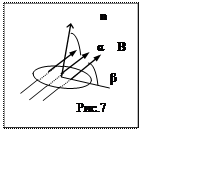Ниже будет показано, что произведение индуктивности и тока дает потокосцепление (L·I = Ψ), отсюда Гн·А = Вб.

    Ответ: циркуляция вектора В равна 25,12·10^-7 Тл·м.

    Из формулы (3.2.3), как следствие, вытекает формула для расчета магнитной индукции поля на оси бесконечно длинного соленоида в его середине:

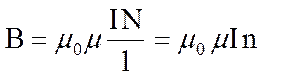                                                                            (3.2.4)                          

где N – общее число соленоида; l – его длина ; n = N /l– число витков на единицу длины, μ – магнитная проницаемость сердечника, (если сердечника нет или он немагнитный, то μ =1).

3. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ

    ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ. РАБОТА СИЛ ПОЛЯ                                                           

    Рассмотрим последовательно, как магнитное поле действует сначала на движущиеся заряды, затем на проводники с токами, в том числе и на рамку с током. В общем  случае электромагнитное поле характеризуется векторами Е(r,t) – напряженностью электрического поля и  В(r,t) – магнитной индукцией. Сила, действующая на заряженную частицу, движущуюся в электромагнитном поле,

                                            F = q E + q [ v,B],                                           (3.3.1)

называется силой Лоренца. Квадратные скобки означают векторное произведение двух векторов v  и  B.

    Выражение (3.3.1) справедливо как для постоянных, так и переменных электромагнитных полей. С магнитным полем связана та часть силы, которая проявляется только при движении заряда (см. второе слагаемое в выражении (3.3.1)), т.е.

                                                    F_m = q [v,B],

в скалярной форме:

                              F_m =q v B sin(v^В).                                         (3.3.1΄)

    Направление силы Лоренца можно определить по правилу векторного произведения, которому соответствует мнемоническое правило правой тройки: большой , указательный и средней пальцы правой руки надо расположить перпендикулярно друг другу; если направить большой палец по вектору v для положительного заряда (для отрицательного против v), указательный по вектору В, то средний палец покажет направление магнитной составляющей силы Лоренца F_m. Есть и другой способ -  мнемоническое правило левой руки. Для q > 0 левую руку надо расположить так, чтобы линии вектора В входили в ладонь, четыре пальца направить по направлению вектора v(рис. 9). Тогда большой палец укажет направление силы Лоренца. Если q < 0, левую руку надо развернуть так, чтобы линии вектора В выходили из ладони.

    Под действием силы Лоренца заряженная частица закручивается вокруг силовых линий поля: положительная частица – по часовой стрелке, отрицательная – против часовой стрелки, если смотреть навстречу силовым линиям поля.