Магнитное поле: Краткая теория и образцы решений некоторых задач, страница 3

    Пример. Частица массой m, несущая заряд q, влетает в однородное мегнитное поле перпендикулярно линиям вектора В (рис. 10). Определить радиус окружности, период и круговую частоту заряженной частицы.

     Решение. Магнитная составляющая силы Лоренца искривляет траекторию частицы, но не выводит ее из плоскости, перпендикулярной к полю. Абсолютная величина скорости не изменяется, сила остается постоянной, поэтому частица движется по окружности. Приравняв магнитную составляющую силы Лоренца к центробежной силе

                                          qvB = mv² / R,

получим для радиуса частицы равенство

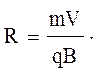                                                                                                       (3.3.2)

Период обращения частицы

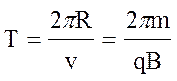                                                    .                                           (3.3.3)

Круговая частота ω обращение частицы, то есть число оборотов за 2π секунд,

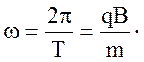                                                                                                (3.3.3 ^΄ ).

    Ответ : R = mv/ (qB); ω = qB/ m; для конкретного типа частиц период и частота зависят только от индукции магнитного поля.

	Рис.9		Рис.10

 

    Рассмотрим движение частицы, движущейся под углом < 90° к направлению линий вектора В (рис. 11). Определим шаг витка спирали h. Скорость v имеет две составляющие, одна из которых v_çç = v cosβ,параллельна В, другая v_^ =        v sin β – перпендикулярна линиям магнитной индукции В.

При движении частицы вдоль линий В магнитная составляющая силы равна нулю, поэтому вдоль поля частица движется равномерно со скоростью

                                             v_çç = v cosβ. 

                                 Шаг витка спирали

                                           h =  v_ççТ = v Т соsβ.

Подставив выражение для T из формулы (1.3.3), получим :

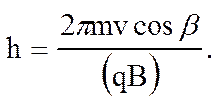                                                                                       (3.3.4)

 

                                                         Рис.11

На  элемент проводника с током Idl в магнитном поле действует сила  Ампера.

                                                                                                                            

или в скалярной форме

                                              dF = I dl B sinα,                                              (3.3.5)

где α – угол между элементом проводника и магнитной индукцией.

Для проводника конечной длины необходимо взять интеграл :

                                                F = I ∫ [dl, B].                                              (3.3.6)

Направление силы Ампера, как и силы Лоренца (см. выше), определяется по правилу левой руки. Но с учетом того, что четыре пальца здесь направляют вдоль тока.

    Пример. Проводник в виде полукольца радиусом R = 5 см (рис. 12) помещен в однородное магнитное поле, силовые линии которого направлены от нас (изображены крестиками). Найти силу, действующую на проводник, если сила тока, текущего по проводнику, I = 2 А, а индукция магнитного поля В = 1 мкТл.

    Решение. Воспользуемся формулой (3.3.6), учитывая, что под интегралом стоит векторное произведение, а значит, в конечном счете, векторная величина. Сумму векторов удобно находить, проектируя векторов – слагаемые на оси координат и складывая их проекции. Поэтому, решая задачу в скалярной форме, интеграл можно представить в виде суммы интегралов :

                                           F = ∫ dF_i,     F = ∫ dF_х + ∫ dF_у.

По правилу левой руки находим векторы сил dF, действующих на каждый элемент проводника (рис. 12).

	Рис.12

 

Первый интеграл в правой части равен нулю, т. к. сумма проекций dF равна нулю, как следует из рисунка: из–за симметрии картины каждой положительной проекции соответствует отрицательная такой же величины. Тогда искомая сила равна только второму интегралу

F = ∫ dF_у = ∫ dF cosβ,

где β – угол между векторами dF и осью ОΥ, а элемент длины проводника можно представить как dl = R cos β. Так как угол отсчитывается от оси ОΥ влево и право, то пределами интегрирования будут значения – 90 ⁰ и 90 ⁰  . Подставляя dl в dF и решая второй интеграл, получим

                             F =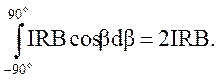  

Численный расчет дает : F = 2 ·  2 А ·10^-6 Тл ·  0,05 м = 2 · 10^-7 Н.

    Ответ:F = 2 · 10^-7 Н.

     Закон Ампера дает выражение для силы, с которой взаимодействуют два бесконечно длинные параллельные друг другу проводника с токами, находящимися на расстоянии b друг от друга:

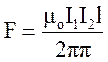                                                                                                        (3.3.7)

     Можно показать, что проводники с токами, текущими в одну сторону, притягивается, и отталкивается в случае антипараллельного направления токов.

     На рамку (контур) с током в магнитном поле действуют силы. Которые стремятся повернуть ее так. Чтобы магнитный момент Р_m рамки совпадал с направлением магнитной индукции. При этом вращающий момент М , действующий  на контур площадью S с током  I , равен

                                                     M = I S B sinα,                                           (3.3.8)

где  α – угол между магнитной индукцией и нормалью к рамке. В векторной форме

                                                   M = [ P_m, B].

    Положение, в котором угол  α = 0 ⁰. называют устойчивым равновесием, а положение с  α = 180 ⁰  - неустойчивым равновесием.

    Элементарная работа магнитного поля при повороте рамки на угол α

dA = I dФ,

а при повороте рамки на конечный угол, из положения 1 в положение 2 совершается работа :