Методические указания по дисциплине «Основы теории надежности», страница 9

Доверительная вероятность b – это вероятность того, что случайный интервал I_β накроет параметр а.

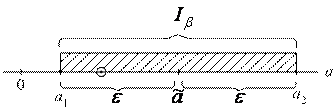
I_β – доверительный интервал. .

Методические указания

1. Вычисляется оценка (среднее значение):

,

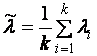где k – число значений случайной величины λ, k=10.

2. Определяется несмещенная оценка  (дисперсия, вычисленная по опытным данным):

.

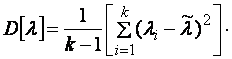3. Дисперсия выборочной средней величины

.

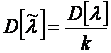4. Определяется оценка σ (среднеквадратичное отклонение):

.

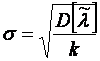5. По табл. 3.1 для заданного варианта определяется величина b.

6. Определяется отклонение ε:

,

где b – доверительная вероятность.

Для определения ε необходимо знать функцию, обратную функции Лапласа, , т.е. аргумент по значению функции. Функция Лапласа в зависимости от значений аргумента задана в табл. 3.2.

7. Определяются нижняя и верхняя доверительные границы доверительного интервала

.

8. Аналогично определяются доверительные интервалы для числовых оценок параметра P(t),Q(t), f(t).

9. Полученные интервалы наносятся на графики, построенные в пункте 1.

Таблица 3.1

Значения доверительной вероятности b

Номер варианта	1	2	3	4	5	6	7	8	9	10
Значение доверительной вероятности β	0,8	0,82	0,81	0,83	0,85	0,87	0,9	0,92	0,93	0,95
Номер варианта	11	12	13	14	15	16	17	18	19	20
Значение доверительной вероятности β	0,9	0,92	0,93	0,95	0,9	0,91	0,93	0,95	0,92	0,93
Номер варианта	21	22	23	24	25	26	27	28	29	30
Значение доверительной вероятности β	0,87	0,86	0,8	0,82	0,81	0,83	0,91	0,9	0,92	0,95