Исследование вольт-амперной характеристики полупроводникового нагревателя в вакууме, страница 5

Формулу (14) также называют законом Ома в дифференциальной форме.

Сравним теперь формулу (14) с хорошо известным выражением для плотности тока j в виде:

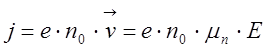. (15)

В формуле (15) n₀ — концентрация свободных электронов в полупроводнике n-типа. Для дырочного полупроводника вместо n₀войдет концентрация дырок p₀, а вместо подвижности электронов µ_п— дырочная подвижность µ_p.

Из формул (14) и (15) следуют выражения для проводимости полупроводников n-и р-типа:

a)  ;

b)  . (16)

Вычислять значения концентрации электронов и дырок мы умеем для самых разных случаев; и для собственного полупроводника, и для примесных, и для случая примесного истощения. С поведением подвижности мы также хорошо знакомы. Таким образом, мы можем теперь анализировать проводимость полупроводников в самых разных, даже довольно сложных случаях.

3.  Экспериментальная часть.

3.1  Описание установки.

Экспериментальная установка представляет собой источник напряжения, который подает напряжение на кремниевый нагреватель, расположенный в вакуумной установке. Кремниевый нагреватель, лежащий на кварцевой шлифованной подложке, подключен к источнику с помощью графитовых контактов, которыми нагреватель прижат к подложке. Также в схему включен амперметр который измеряет ток в цепи. С помощью этой установки мы получим вольт-амперную характеристику.

Рис.2. Фотография установки.

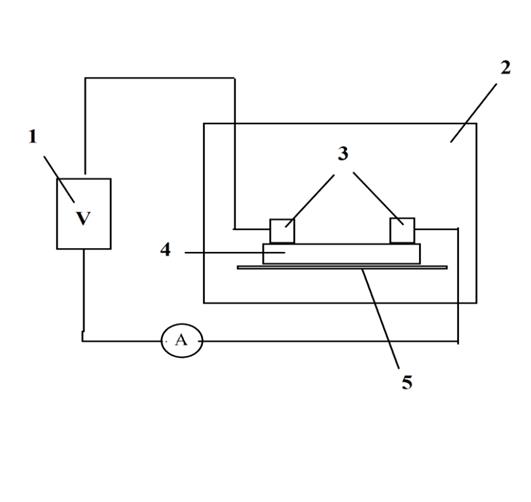
Рис. 3. Схема установки: 1 – источник напряжения, 2 – вакуумная установка, 3 – графитовые контакты, 4 – кремниевый нагреватель, 5 – кварцевая шлифованная подложка.

3.2  Методика измерений.

Используя установку мы, постепенно увеличивая напряжение на кремниевом нагревателе, снимаем на амперметре ток и получим вольт-амперную характеристику. Также практический интерес имеет получение графика зависимости σ(T).

Для того чтобы получить температуру T из вольт-амперной характеристики сначала мы посчитаем мощность выделяемую на нагревателе по всем известной формуле:

.(17)

Если пренебречь тепловыми потерями, то та же мощность равна мощности потока излучения нагревателя, которая считается по формуле:

, (18)

где S – площадь излучающей поверхности, ε – коэффициент черноты, k – постоянная Больцмана, T – температура. И из формул (17) и (18) получим выражение для температуры:

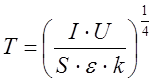 (19).

Для того чтобы найти проводимость воспользуемся законом Ома:

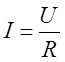. (20)

А также выразим сопротивление через следующую формулу:

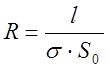, (21)

где S₀ – площадь поперечного сечения кремниевого нагревателя, l – длина нагревателя. Из формул (20) и (21) получим формулу для проводимости:

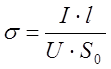. (22)

Далее из полученных данных построим график σ(T) и ln σ (1/T).

3.3  Результаты.

В результате проведенного эксперимента получили вольт-амперную характеристику представленную на следующем рисунке:

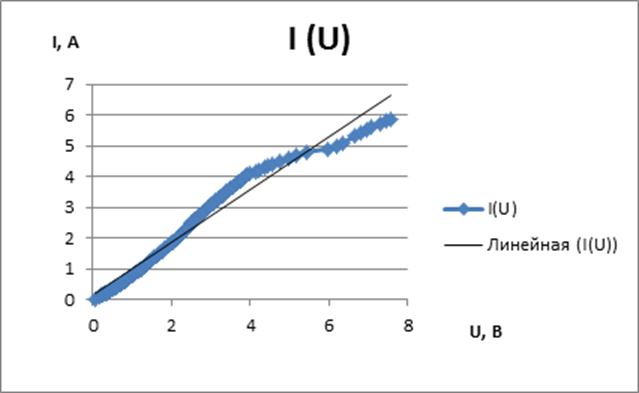
Рис. 4. Вольт-амперная характеристика кремниевого нагревателя в вакууме.

Используя формулы (19) и (22) и известные нам параметры кремниевого нагревателя (ε = 0,8; l = 5 см; S = 3*10^-4 м²; S₀=12*10^-6 м²) получим графики σ(T) и ln σ (1/T):

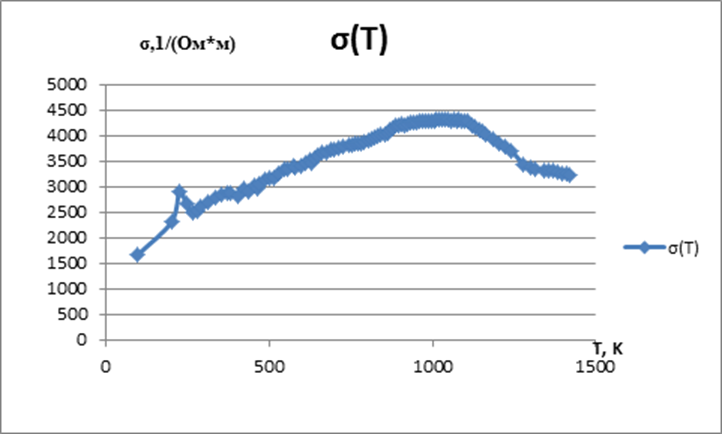
Рис. 5. График зависимости проводимости от температуры.

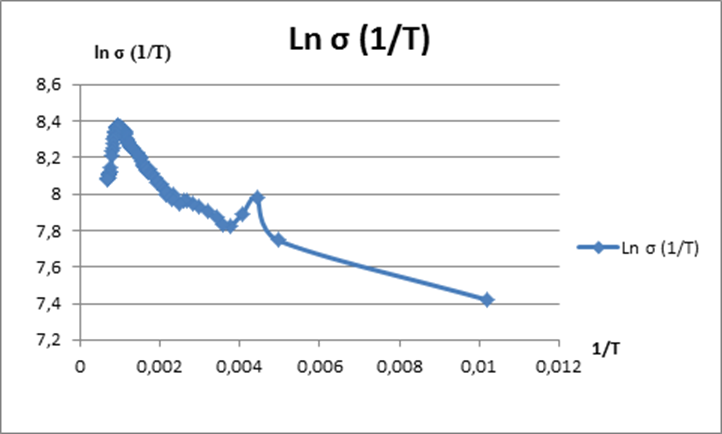
Рис. 6. График зависимости логарифма проводимости от обратной температуры.

4.  Обсуждение результатов

Взглянув на вольт-амперную характеристику можно сказать что наш образец содержит достаточно большое количество примесей, но не является вырожденным.

Также рассматривая рис. 5 и 6 можно сказать, что падение проводимости при высоких значениях температуры связано с тем, что примесная концентрация выходит на постоянное значение, а подвижность падает. Если бы в нашем образце было меньше примесей, то при повышении температуры после падения проводимости мы увидели бы рост проводимости, за счет увеличения собственной концентрации носителей. Также выразив проводимость через формулы (16), (7), (10) и (12), и (5) мы можем заметить что форма теоретической кривой соответствует полученной нами на рис. 5 и 6.

Также взглянув на рис. 5 мы заметим, что значения температуры слишком велики. В реальности температура ниже, потому что температура плавления кремния: T ≈ 1400 K. Данное несоответствие связано с тем, что в наших расчетах мы не учитывали потери энергии, потому что не вся мощность выделяемая на нагревателе уходит в излучение.

5.  Выводы

Итак, в результате эксперимента мы получили график вольт-амперной характеристики, необходимую нам для контроля мощности, выделяемой на нагревателе. Так как полученная зависимость близка к линейной, мы можем сказать, что наш нагреватель содержит большое количество примесей. На основе полученной вольт-амперной характеристики мы построили графики зависимости проводимости от температуры. Однако использованный нами метод в эксперименте не позволяет получить точную зависимость проводимость от температуры, но позволяет оценить вид графика.

6.  Список использованной литературы

1.   Володин В.А. Физические основы микроэлектроники: Курс лекций / Новосиб. гос. ун-т. Новосибирск, 2009. 192 с.

2.   Левинштейн М.Е., Симин Г.С. Знакомство с полупроводниками/Под ред. Л.Г. Асламазова. – М.: Наука. Главная редакция физико-математической литературы, 1984. – 240 с. – (Библиотека <<Квант>>. Вып. 33). – 40 к.

3.  Левинштейн М.Е., Симин Г.С. Барьеры (От кристалла до интегральной схемы). – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 320 с. – (Б-чка <<Квант>>, Вып. 65.)