Исследование вольт-амперной характеристики полупроводникового нагревателя в вакууме, страница 4

Формула (10) является не точной, а приближенной. Она справедлива только тогда, когда рассчитанное по ней значение n_dмного меньше, чем концентрация введенных примесей N_d, т.е. когда  << Δε. Когда температура Ттак высока, что величина  ~ Δε,все примесные атомы оказываются ионизованными и концентрация примесных электронов просто равняется N_d. Это явление носит название примесного истощения — термин довольно естественный. При достаточно высокой температуре все атомы примеси отдали “лишние” электроны и источник примесных электронов истощился. Дальнейший нагрев кристалла не приводит к росту концентрации примесных электронов. При повышенных температурах собственная концентрация электронов значительно превышает концентрацию примесных. Проводимость кристалла снова определяется не концентрацией введенной примеси, а собственными свойствами полупроводника.

Рассказ о полупроводниках n-типа будет не полон, если мы оставим без внимания вопрос, что произойдет с дырками в полупроводнике, в который введена донорная примесь.

Прежде всего нужно отметить, что когда атом донора ионизуется и отдает свободный электрон, никакой дырки не образуется. Атом мышьяка в решетке кремния, например, отдав пятый валентный электрон, остается связанным с соседними атомами кремния четырьмя полноценными связями. Никакой свободной связи, на которую могли бы перемещаться электроны с соседних орбит, нет. Дырка не образуется.

На первый взгляд может показаться, что дырок в электронном полупроводнике будет тогда столько же, сколько и в совершенно чистом, собственном. Однако это не так, в действительности, при данной температуре Т каждую секунду в электронном полупроводнике рвется электронных связей между атомами и образуется электронно-дырочных пар ровно столько же, сколько и в собственном. Но гибнут дырки гораздо чаше, ведь в электронном полупроводнике свободных электронов гораздо больше, чем в собственном. В результате дырок в полупроводнике n-типа оказывается меньше, чем в собственном полупроводнике. Существует очень простая формула, связывающая равновесную концентрацию дырок p и электронов п в полупроводнике:

, (11)

где n, — собственная концентрация носителей при температуре Т, определяемая выражением (5). Из формулы (11) следует, что чем больше электронов, тем меньше дырок.

Примесные полупроводники. Акцепторная примесь.

Изучим теперь другую  ситуацию, а именно: в полупроводник введена примесь, которая не отдает, а легко отбирает электроны у соседних атомов.

Теперь примесью в кремнии является не мышьяк, а бор. Бор трехвалентен — на внешней электронной оболочке у него находятся три электрона. Чтобы образовать полноценную связь с соседними атомами кремния, одного электрона ему не хватает. Для того чтобы дырка перемещалась по кристаллу, никакой энергии не требуется. Атом бора—чужак в решетке кремния. Для того чтобы электрон от соседнего атома кремния перешел к бору, необходимо затратить энергию Δε. Эта энергия — энергия активации, невелика, но все-таки не равна нулю. Пока этот, пусть небольшой, энергетический барьер не перейден, дырки в кристалле нет.

Предположим, однако, что тепловые колебания решетки или квант света сообщили необходимую энергию, и электрон с соседнего атома кремния перешел к бору. Пустая связь образовалась у атома кремния и возникла дырка — свободный носитель положительного заряда, способный переносить электрический ток. Акцепторная примесь создает в кристалле полупроводника свободные носители тока — дырки.

Теперь мы могли бы слово в слово переписать предыдущие рассуждения, посвященные описанию электронного полупроводника, заменяя слово «электрон» словом «дырка».

Пусть в каждый кубический сантиметр кристалла введено N_a атомов бора. Рассмотрим сначала самую простую ситуацию — температура кристалла Т= 0 К. Ясно, что в этом случае кристалл представляет собой идеальный диэлектрик: как ни мала энергия активации Δε, требуемая, чтобы перевести электрон от атома кремния к атому бора и образовать дырку, при нулевой температуре ей взяться неоткуда.

Если температура кристалла отлична от нуля, то равновесная концентрация примесных дырок p определится из выражения, аналогичного формуле (10):

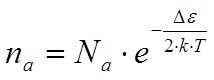 (12)

и т. д.

Cитуации с донорной и акцепторной примесью очень похожи. Типичный диапазон концентраций примесных атомов для акцепторной примеси такой же, как и для донорной. Так же, как и в случае донорной примеси, величина Δε для дырки уменьшается с ростом N_aи при достаточно больших значениях N_aобращается в нуль. Поскольку величина Δε гораздо меньше, чем энергия образования электронно-дырочной пары ε_g, то концентрация примесных дырок р_абудет значительно больше, чем концентрация собственных. При более высоких температурах, когда  ~ Δε, наступает явление примесного истощения. Наконец при еще более высоких температурах собственная концентрация, определяемая формулой (5), превысит примесную. В дырочном полупроводнике увеличение концентрации дырок сопровождается уменьшением концентрации электронов. Количественное соотношение между концентрациями электронов и дырок одинаково справедливо и для n- и для р-типа полупроводников.

Закон Ома в дифференциальной форме. Проводимость.

Установим несколько простых соотношений, вытекающих из закона Ома. Пусть к образцу длиной l, имеющему поперечное сечение S и изготовленному из материала с удельным сопротивлением ρ, приложено напряжение U. Через образец течет ток

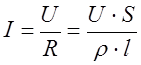. (13)

Учтем, что плотность тока j = I/S, поле в образце E=U/l и введем величину проводимости σ = 1/ρ. Тогда формулу (13) можно переписать в виде:

. (14)