Исследование вольт-амперной характеристики полупроводникового нагревателя в вакууме, страница 2

Хаотическое тепловое движение непрерывно разрывает электронные связи между атомами и создает свободные электроны и дырки. Хаотически блуждая по кристаллу, свободный электрон и дырка могут оказаться рядом. Свободный электрон занимает свое место на свободной траектории межатомной связи. Такой процесс называется рекомбинацией.

В установившемся, стационарном состоянии существует динамическое равновесие: сколько электронов и дырок создается каждую секунду в объеме полупроводника за счет тепловой генерации, столько же их будет гибнуть за счет рекомбинации. В полупроводнике при данной температуре устанавливается определенная равновесная концентрация электронов и дырок. Наша задача – определить, сколько свободных носителей создается в единице объема полупроводника в единицу времени и сколько их гибнет за счет рекомбинации. В условиях равновесия эти две величины должны быть равны. Приравнивая, их друг к другу, мы и определим равновесную концентрацию носителей.

Тепловая генерация электронов и дырок.

Мы уже знаем, в чем состоит главная особенность генерации электронно-дырочных пар под действием теплового движения. Для их образования нужна энергия, значительно превышающая среднюю энергию .

Ситуации, когда для того, чтобы некоторое событие произошло, нужна большая величина энергии Δε, значительно превышающая величину , встречаются при исследовании громадного числа самых разнообразных физических процессов.

Итак, число электронно-дырочных пар K₁, создаваемых каждую секунду в единице объема полупроводника, равняется

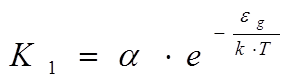 (1)

где α – коэффициент пропорциональности, различный для разных полупроводников. С другой стороны, каждую секунду в той же единице объема исчезнет за счет рекомбинации некоторое число носителей K₂.

Рекомбинация электронов и дырок.

Для того чтобы рекомбинировать, электрон и дырка должны встретиться. Обсудим, от чего зависит частота таких встреч. Проделаем следующий мысленный эксперимент. Будем следить за каким-нибудь атомом кристаллической решетки, и отмечать появление в его окрестности, скажем дырки. Ясно, что чем больше дырок имеется в единице объема полупроводника, тем чаще они будут появляться: вероятность появления дырки пропорциональна концентрации дырок p_i. По тем же причинам вероятность появления свободного электрона в окрестностях этого же атома пропорциональна концентрации электронов n_i. Нас интересует вероятность одновременного появления в окрестностях атома и электрона, и дырки. Это вероятность пропорциональна произведению концентраций электронов и дырок . Таким образом, число носителей, рекомбинирующих каждую секунду в единице объема, равняется

. (2)

Коэффициент пропорциональности β, так же, как и α, различный для разных полупроводников.

В собственных полупроводниках, которые мы изучаем, носители генерируются и рекомбинируют всегда парами. Поэтому n_i = p_i, отсюда следует, что

. (3)

Концентрация электронов и дырок в собственном полупроводнике.

Приравнивая число ежесекундно появляющихся паp K₁ числу гибнущих K₂, получим

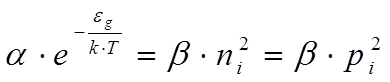. (4)

Отсюда находим, что

,

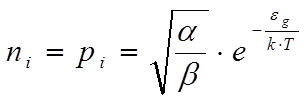или

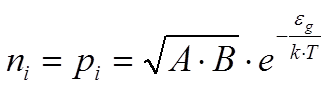. (5)

Величины А и В измеряются в см^-3. Для всех полупроводников, с которыми нам придется иметь дело, значения А и В хорошо известны.

А теперь представим себе, что примесь, попавшая в полупроводник, способна сравнительно легко отдавать свободный электрон или образовывать дырку.

А ведь примеси содержатся и в исходных материалах, из которых получают полупроводниковые кристаллы, и в стенках печей и приборов, где происходит синтез и очистка полупроводников, и в окружающем воздухе.

Движение в электрическом поле.

Если к полупроводнику приложено электрическое поле, то на хаотическое тепловое движение свободных носителей накладывается направленный дрейф частиц вдоль направления поля. Определим скорость этого направления движения.

Если электрическое поле отсутствует, то электрон участвует только в хаотическом тепловом движении. Никакого избранного направления не существует. Поэтому, хотя в промежутке между столкновениями электрон движется с очень большой скоростью, направленное движение отсутствует.

В присутствии электрического поля электроны продолжают свою бешеную пляску. По-прежнему невозможно предсказать, куда полетит носитель после очередного столкновения. Но, куда бы он ни полетел, электрическое поле будет слабо, тянуть его всегда в одном и том же направлении. В результате возникает направленное движение.

В электрическом поле Е на электрон действует сила . Под действием этой силы носитель приобретает вдоль поля ускорение 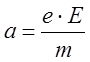. Двигаясь без столкновений, носитель за время tприобретает скорость в направлении поля .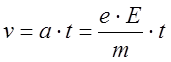

Чтобы правильно вычислить среднюю скорость, приобретаемую носителем в условиях многократных столкновений, нужно помнить о двух обстоятельствах.

Во-первых, как мы уже знаем, непосредственно после столкновения носитель может с равной вероятностью двигаться в любом направлении. Это означает, что скорость направленногодвижения после столкновения равняется нулю. Во-вторых, поскольку процесс столкновения — процесс случайный, носитель в промежутке между двумя последовательными столкновениями проводит “в свободном полете” разное время.

Средняя скорость направленного движения  равняется произведению ускорения на среднее время между столкновениями τ₀:

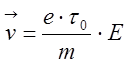. (6)

Таким образом, скорость направленного движения или, как часто говорят, дрейфовая скорость, свободных носителей в кристалле пропорциональна напряженности электрического поля. Коэффициент пропорциональности