
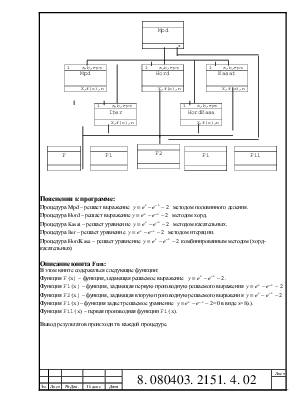





Лабораторна робота №2
розв’язання нелінійних рівнянь
Мета роботи : Навчитися програмувати розв’язання нелінійні рівняння на ЕОМ.
Завдання :
1. Розробити процедури чи функції, що реалізують наступні методи розв’язання нелінійних рівнянь:
a) половинного поділу (дихотомії);
b) простої ітерації;
c) хорд;
d) Ньютона (дотичних);
e) Рафсона (січних).
2. Розв’язати рівняння
![]()
кожним з методів на ЕОМ (з використанням цих процедур і функцій) і порівняти витрати часу. Рівняння і точність розв’язання задається викладачем.
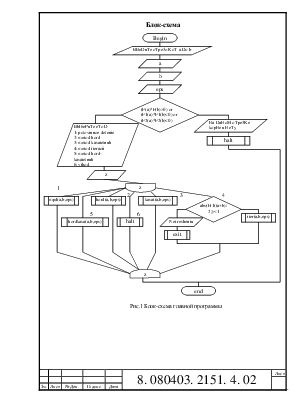
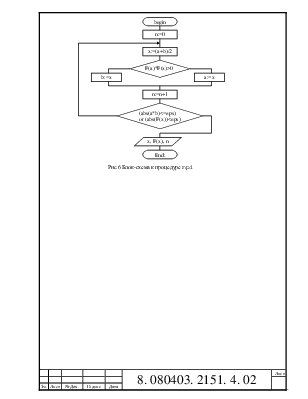
Схема расчетов:
Метод половинного деления.
Основывается на последовательном поиске точки пересечения графика функции и координатной оси OX. Сначала берется произвольный отрезок ab на оси OX. Затем проверяется находится ли внутри него точка пересечения графика с осью. Если нет то следует взять другой отрезок ab.
Проверка осуществляется следующим образом: сравнивается значения функций f(a) и f(b) с нулем. Если знаки функций различны, то в этом отрезке функция пересекает ось OX. Затем для дальнейшего поиска берется точка посреди отрезка ab, например, точка c. Проверяется какой отрезок пересекает функция – aс или cb. Если пересечение на отрезке ac то за точку b берется точка c. Если пересечение на отрезке cb, то за точку a принимается точка с. Поиск продолжается до тех пор пока |a-b|<eps или |f(a)-f(b)|<eps.
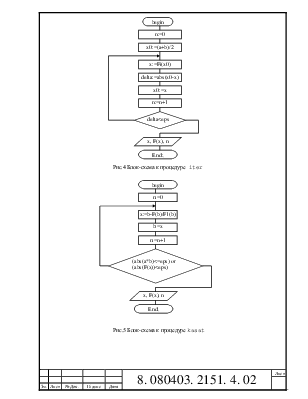
Метод касательных.
При методе касательных первоначально за точку x принимается произвольная точка на графике. Затем ищется точка пересечения касательной с осью OX по формуле x1=x-f(x)/f’(x). Затем находится значение функции f(x1). Если |f(x1)|<=eps, то x1 является решением уравнения, иначе за точку x берется точка x1 и продолжается поиск до тех пор пока условие |f(x1)|<=eps не будет выполнено.
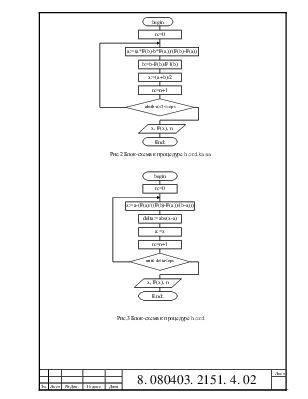
Метод хорд.
При методе хорд сначала определяется локализация корня, то есть отрезок, на котором расположен корень – отрезок ab. При поиске корня через точки (a, f(a)) и (b, f(b)) проводится хорда. Определяется точка пересечения хорды с осью OX – точка c – по формуле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.