Проектирование систем с заданными характеристиками (глава дипломной работы), страница 4

                                                                                                  (5.2.2)

где  - корень квадратный из среднеквадратичного значения (RMS) ширины спектра источника.  - параметр дисперсии [см. уравнение (2.3.5)]. Фактическая величина  зависит от того, насколько близка рабочая длина волны к длине волны нулевой дисперсии волокна и обычно ~ 1 пс/км-нм. Рис. 5.4 показывает, когда начинает преобладать дисперсионный предел для длины волны световой системы 1,3 мкм при  пс/км, при этом  (Гб/с)-км. Как видно, при этих условиях система ограничена потерями при скоростях вплоть до 1 Гб/с и становится ограниченной дисперсией на более высоких скоростях.

          Третье поколение световых систем работает вблизи 1,55 мкм, чтобы использовать преимущество самых малых потерь в этом волновом диапазоне. Однако, дисперсия волокна становится главной проблемой для таких систем, как D » 16 пс/(км-нм) вблизи волны 1,55 мкм для обычных волокон из кремнезема. полупроводниковые лазеры, работающие с одной продольной модой, обеспечивают решение этой проблемы. В конечном счете предел [см. уравнение (2.4.31)] определяется соотношением

                                                                                                    (5.2.3)

где  связано с D уравнением (2.3.5). Рис. 5.4 показывает этот предел при =4000 (Гб/с)²-км. Как видно, идеальная система на волне 1,55 мкм становится ограниченной дисперсией только при B > 5 Гб/с. На практике на оптический импульс оказывает влияние частотный чирп (изменение оптической частоты за время импульса), это происходит при непосредственной модуляции (лазера), что является более серьезным ограничением. Влияние частотного чирпа на характеристики системы рассматривается в разделе 5.4.4. Влияние частотного чирпа учитывается расширением спектра импульса. Если использовать уравнение (5.2.2) при D = 16 пс/(км-нм) и = 0,1 нм, произведение BL ограничено значением 150 (Гб/с) – км*. Таким образом, частотный чирп ограничивает дальность передачи до 75 км при В = 2 Гб/с, хотя предел из-за потерь превышает 150 км. Простое решение проблемы частотного чирпа достигается использованием волокна со сдвинутой дисперсией, в котором дисперсия и потери минимальны вблизи 1,55 мкм. Рис. 5.4 показывает улучшение при использовании уравнения (5.2.3) при = 2 (пс)²/км. Такие системы могут работать на скорости 20 Гб/с при расстоянии между повторителями 80 км. Дальнейшее улучшение возможно только при работе световых систем очень близко к волне нулевой дисперсии – задача, которая требует тщательного согласования длины волны лазера с длиной волны нулевой дисперсии и не всегда выполнима из-за изменения дисперсионных свойств волокна вдоль линии передачи. Практически частотный чирп делает трудно достижимым даже предел, показанный на рис. 5.4. К 1989 г. Два лабораторных эксперимента продемонстрировали передачу на 81 км со скоростью 11 Гб/с [14] и на 100 км при 10 Гб/с, используя полупроводниковые лазеры с малым чирпом и волокно со сдвинутой дисперсией. Треугольники на рис. 5.4 показывают, что эти системы очень близки к основному пределу, соответствующему дисперсии волокна.

5.2.3. Системы дальней связи

с линейными усилителями.

          С появлением оптических усилителей стало возможным компенсировать потери в волокне периодически включением усилителей в волоконных линиях дальней связи (см. рис. 5.1). В то же время влияние дисперсии групповой скорости (GVD) может быть уменьшено, либо работая близко к волне нулевой дисперсии, либо используя схемы компенсации дисперсии (см. главу 9). Так как при этом ни потери в оптическом кабеле, ни дисперсия волокна не являются ограничивающими факторами, в конечном счете, длину лини может ограничить число последовательно включенных линейных усилителей. Этот вопрос рассматривается в разделе 8.6, который посвящен легированным эрбием волоконным усилителям. В этом разделе основное внимание уделяется факторам, которые ограничивают качество волоконных линий с усилителями и дается несколько рекомендаций по проектированию.

          Наиболее важный фактор при проектировании линий с усилителями связан с нелинейными явлениями в оптическом волокне [16], рассмотренными в разделе 2.6. Для одноканальных световых систем доминирует в наибольшей степени нелинейное явление, ограничивающее показатели качества, называемое само-модуляцией фазы – SPM. Когда используются оптоэлектронные регенераторы, этот эффект накапливается только в одном интервале между повторителями (типично < 100 км). SPM не оказывает существенного влияния, когда передаваемая мощность соответствует уравнению (2.6.8) или мощность на входе волокна Р_ВХ = P_in £ 45 мВт. Для сравнения, это воздействие накапливается при больших расстояниях (~ 1000 км), когда усилители используются периодически для компенсации потерь. Грубую оценку ограничения, обусловленного SPM, можно получить из уравнения (2.6.7), заменив L_eff на общую длину линии L_T, а P_in – на среднюю мощность одного усилителя. Условие фNL<<1 при этом ограничивает общую длину линии до L_T £ L_NL, где нелинейная длина (L_NL) находится как  и g - нелинейный параметр, определяемый соотношением (2.6.6). Обычно 1 (Вт)^—1, а длина линии ограничена значением меньше 1000 км, когда = 1 мкВт.

          Приведенная оценка ограничения, обусловленного SPM, является упрощенной, так как полностью игнорирует роль дисперсии волокна. Фактически явления дисперсии и нелинейности действуют на оптический сигнал одновременно, и их взаимное переплетение становится очень важным фактором [16]. Влияние SPM на распространение импульса                                                                                                                                              в соответствии с уравнением (2.4.9), которое при этом становится

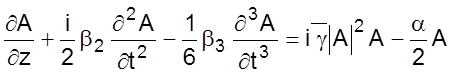                                                           (5.2.4)

Уравнение (5.2.4) отличается от (2.4.9) тем, что «0» в правой части заменен двумя членами, учитывающими нелинейность -  и затухание - . А – амплитудное значение величин, характеризующих электромагнитное поле в волокне. В уравнении (5.2.4)  (затухание) учитывается последним членом. Это уравнение также используется при рассмотрении солитонов в главе 10.