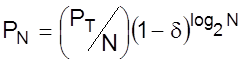Проектирование систем с заданными характеристиками (глава дипломной работы), страница 3

                                                                                         (5.1.2)

где d представляет собой потери в соединениях каждого направленного соединителя. Если d = 0,05, Р_Т = 1 мВт, P_N = 0,1 мквт для иллюстрации, N может быть такой же большой                                                      Эта величина N должна быть сравнимой                                                      со случаем шинной структуры, характеризуемой уравнением (5.1.1). Относительно большая величина N делает звездную структуру более привлекательной для использования в LAN. LAN рассматриваются в главе 7, которая посвящена многоканальным системам связи. В оставшейся части данной главы рассматриваются, главным образом, конструкции и характеристики линий, которые составляют основной элемент всех систем связи, включая LAN и сети распределения.

5.2. Рекомендации по проектированию.

          Проектирование оптоволоконных систем связи требует ясного понимания ограничений, обусловленных потерями, дисперсией и нелинейностью волокна. Так как свойства волокна зависят от длины волны, то выбор длины волны является основным вопросом проектирования. В этом разделе оценим, как скорость в битах и дальность передачи ограничивается потерями в волокне, дисперсией и нелинейностью. Раздел также показывает прогресс, реализованный в разработках наземных и подводных световых систем, достигнутый с 1977 года, когда были завершены первые полевые испытания.

5.2.1. Световые системы,

ограничиваемые потерями.

          За исключением некоторых коротких линий между пунктами, используемых в сетях внутри зданий, потери в волокне играют важную роль в конструировании систем. рассмотрим оптический передатчик с отдаваемой средней мощностью  (tr – передатчик). Если сигнал детектируется приемником, который требует средней входной мощности  (rec – приемник) при скорости В, максимальная дальность передачи ограничивается соотношением:

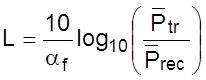                                                                                              (5.2.1)

где a_f – чистые потери (затухание) (в дБ/км) волоконного кабеля, включая потери в сварках и соединителях. Зависимость L от скорости в битах обусловлена линейной зависимостью  от скорости в битах, так как

                                         ,

где  - энергия фотона и  - среднее число фотонов на бит, необходимое приемнику [cм. уравнение (4.5.24)]. Таким образом, L уменьшается логарифмически от В (обратно логарифму от В) при выбранной длине волны.

          Сплошные линии на рис. 5.4 показывают зависимость L от В для трех обычно используемых длин волн 0,85, 1,3, 1,55 мкм при значениях затухания a_f соответственно равных 2,5, 0,4 и 0,25 дБ/км. Мощность передатчика принята равной = 1 мВт в то время, как для трех длин волн = 300 при l = 0,85 мкм из-за относительно большего затухания для этой длины волны. Расстояние между повторителями в этом случае ограничено значениями 10 – 30 км в зависимости от скорости передачи. Для сравнения расстояние между повторителями 100 км и более возможно для системы, работающей при длине волны вблизи 1,55 мкм.

          Интересно сравнить ограничение из-за потерь на волне 0,85 мкм в световых системах с таким же ограничением в электрических системах, использующих коаксиальный кабель. Точечная линия на рис. 5.4 показывает зависимость L от скорости в битах для коаксиальных кабелей в предположении, что потери возрастают пропорционально . Дальность передачи больше для коаксиальных линий при малых скоростях (В < 5 Мб/с), но оптоволоконные системы имеют преимущество при скоростях больше 5 Мб/с. Так как большая дальность передачи означает меньшее число повторителей в линиях дальней связи, оптоволоконные системы связи дают экономическое преимущество при рабочих скоростях больше 10 Мб/с.

5.2.2. Ограничение световых систем дисперсией.

          В разделе 2.4 показано, как дисперсия волокна ограничивает произведение скорости в битах на расстояние из-за расширения (увеличения длительности) импульса. Когда ограниченные дисперсией расстояния становятся меньше, чем из-за потерь в соответствии с уравнением (5.2.1), систему считают ограниченной потерями. Пунктирные линии на рис. 5.4 показывают ограниченные дисперсией расстояния в зависимости от скорости в битах. Так как физические явления, приводящие к дисперсии, могут быть различными для различных длин волн, рассмотрим каждый случай отдельно.

          Сначала рассмотрим световые системы на длине волны 0,85 мкм, которые часто используют многомодовые волокна, чтобы уменьшить стоимость. Как рассмотрено в разделе 2.1, максимально ограничивающим фактором в многомодовых волокнах является межмодовая дисперсия. Для многомодового волокна со ступенчатым изменением коэффициента преломления уравнение 2.1.6 дает примерную верхнюю границу произведения BL. Немного более точное условие:

                                         *                    

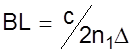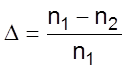
показано на рис. 5.4 при типичных параметрах n₁= 1,46 и D = 0,01. Даже при низких скоростях 1 Мб/с такие многомодовые системы ограничены дисперсией и их дальность передачи ниже 10 км. По этой причине многомодовые волокна с шаговым изменением индекса редко используются в оптоволоконных системах связи. Значительное улучшение достигается при использовании градиентных волокон, для которых междумодовая дисперсия ограничивает произведение BL до значений, определяемых уравнением (2.1.11). Условие 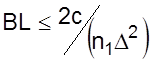 использовано для расчета графика на рис. 5.4. График показывает, что световые системы на волне 0,85 мкм при использовании градиентных волокон скорее ограничены потерями, чем дисперсией, до скоростей 100 Мб/с (0,1 Гб/с). Первые поколения наземных систем связи использовали это преимущество градиентных волокон. Первая коммерческая система появилась в 1980 году и работала на скорости 45 Мб/с при расстоянии между повторителями в 10 км.

          Второе поколение световых систем использовало преимущественно одномодовые волокна вблизи волны 1,31 мкм, соответствующей наименьшей дисперсии. Самым сильным ограничивающим фактором для таких систем является расширение импульсов, обусловленное дисперсией, которая связана также с шириной спектра источника (импульсов). Как показано в разделе 2.4.3, произведение BL при этом ограничено [см. уравнение (2.4.26)] значением