


Изучим работу n-канальной СМО с отказами (n≥1), на вход которой поступает простейший поток заявок Пвх с интенсивностью l, а время TOб обслуживания каждым каналом одной заявки распределено по показательному закону: f (t)=me-mt
Тогда "поток обслуживаний" Поб каждым каналом будет простейшим с интенсивностью m= 1/ ТОб, где ТОб — среднее время обслуживания одной заявки одним каналом.
Задача исследования таких СМО впервые возникла в области телефонии и была решена в 1909 г. А.К. Эрлангом.
Состояния системы занумеруем по числу занятых каналов. Для СМО с отказами это означает, что мы нумеруем состояния по числу заявок, находящихся в системе, т.е. под обслуживанием, поскольку каждый канал в любой момент времени либо свободен, либо обслуживает только одну заявку. Таким образом, СМО может находиться только в одном из следующих n + 1 состояний:
S0 — все я каналов свободны,
S1— занят только один канал, остальные n-1 каналов свободны,
. . .
Sk — заняты k каналов, остальные n-k каналов свободны,
. . .
Sn — заняты все n каналов.
Граф состояний СМО представлен на рис. 4.1.
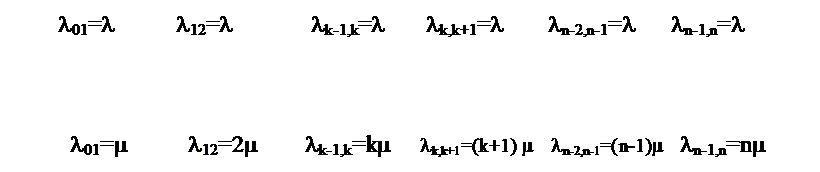 |

Если СМО находится в состоянии sk (k =0,1,...,n-1), т.е. когда k каналов заняты обслуживанием заявок, а остальные n-k каналов свободны, то перескок ее в состояние Sk+1 происходит при поступлении на вход новой заявки. Таким образом, по стрелкам слева направо из любого состояния в соседнее состояние справа систему переводит один и тот же входящий поток заявок Пвх с интенсивностью l. Следовательно, плотность вероятности перехода lk,k+1 (0,1,…,n-1) из любого k-то состояния в (k+1)-е состояние равна l:
l01=l12=…=ln-1=l , (4.1)
что и проставлено над стрелками слева направо.
Так как по предположению входящий поток Пвх простейший, то он является ординарным, т.е. заявки поступают по одной. Поэтому СМО, меняя свои состояния слева направо, не может перескочить через состояние, а переходит только в соседнее справа состояние. По этой причине на графе (см. рис.4.1) отсутствуют стрелки, перескакивающие через состояния слева направо.
Вероятность того, что одновременно, точно в один и тот же момент, освободятся более одного канала, пренебрежимо мала, т.е. такие события практически невозможны. Поэтому на графе нет стрелок, "перескакивающих" через состояния справа налево.
Исходные параметры СМО и характеристики эффективности ее функционирования представлены в табл. 4.1. и 4.2.
Таблица 4.1
|
№ п/п |
Параметры |
Обозначения, значения, формулы |
|
1 |
Число каналов |
N≥ 1 |
|
2 |
Интенсивность простейшего входящего потока заявок Пвх |
In Пвх =l = const (l не зависит от времени t) |
|
3 |
Производительность каждого канала — интенсивность простейшего "потока обслуживания" Поб. (среднее число заявок, обслуживаемое одним каналом за единицу времени при непрерывной его работе без простоя) |
in Поб=m= const (m не зависит от времени t) |
|
4 |
Непрерывная случайная величина Тоб -время обслуживания одной заявки одним каналом, распределена по показательному закону с параметром m |
f (t)=me-mt (t≥0) |
Таблица 4.2
Предельные характеристики эффективности
функционирования n-канальной СМО с отказами
|
№ п/п |
Предельные характеристики |
Обозначения, формулы |
||||
|
1 |
Вероятности состояний СМО pk , k =0, 1, ...,n, выраженные через интенсивность входящего потока l и интенсивность потока обслуживании m |
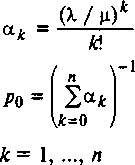
|
||||
|
2 |
Приведенная интенсивность входящего потока — трафик (показатель нагрузки СМО) |
P=l/m=lTоб= Tоб/T, где Тоб - среднее время обслуживания одной заявки одним каналом; Т - средний интервал времени между двумя соседними заявками во входящем потоке |
||||
|
3 |
Вероятности состояний СМО pk , k = 0,1,..., n, выраженные через трафик р |
|
||||
|
4 |
Вероятности состояний СМО pk , k = 0,1,..., n, выраженные через средние времена Т и Тоб |
|
||||
|
5 |
Вероятность отказа ротк |
pотк=pn=(pn/n!)p0 |
||||
|
6 |
Вероятность того, что пришедшая заявка будет обслужена |
Pоб=1-pотк=1-pn |
||||
|
7 |
Относительная пропускная способность |
Q= Pоб=1-pn |
||||
|
8 |
Абсолютная пропускная способность |
A=lQ=l(1- pn) |
||||
|
9 |
Интенсивность выходящего потока Пвых обслуженных заявок |
n=A=l(1- pn) |
||||
|
10 |
Среднее число занятых каналов |
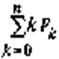
|
||||
|
11 |
Среднее время пребывания заявки в СМО (формула Литтла) |
Tсис=(1/m)*(1-pn)=(1/l)*K=(1/l)*Nсис |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.