Многоканальная СМО с ожиданием и ограничением на длину очереди

Многоканальная СМО с ожиданием

 и ограничением на длину очереди

В этом параграфе рассмотрим n-канальную (n ≥ 1) СМО с ожиданием, максимальное число мест в очереди которой равно m≥ 1. Пусть на вход СМО поступает простейший поток заявок П_вх с интенсивностью λ. Поток обслуживаний П_об каждым каналом также простейший с интенсивностью μ.

Так как указанные потоки стационарны, то  λ и μ не изменяются с течением времени. Заявка, поступившая в СМО в момент, когда в очереди уже стоят m заявок, получает отказ и покидает систему.

Занумеруем состояние системы по числу заявок, находящихся в СМО, как в очереди, так и под обслуживанием:

s₀ – в СМО нет заявок, т.е. все n каналов свободны;

s₁ – в СМО одна заявка, т.е. занят 1 канал, остальные свободны;

…

s_k – в СМО k(< n) заявок, т.е. заняты k каналов, а остальные n-k свободны;

…

s_n – в СМО n заявок, т.е. все n каналов заняты, очереди нет;

s_n+1 – в СМО n + 1 заявка, т.е. все n каналов заняты и одна заявка – в очереди;

…

s_n+r – в СМО n + r заявок, т.е. все n каналов заняты и в очереди стоят r заявок;

…

s_n+m – в СМО n + m заявок, т.е. все n каналов заняты и m заявок стоят в очереди.

Таким образом, данная СМО может находится в одном из n + m + 1 состояний. В состояниях s₀, s₁, …, s_n очереди нет. Размеченный граф состояний рассматриваемой системы изображен на рис. 7.1.

 

                              …                    …                                        …                    …

Рис. 7.1.

Переходы СМО из состояния в состояние по стрелкам слева направо происходят под воздействием одного и того же входящего потока П_вхзаявок с интенсивностью λ. Поэтому плот­ности вероятностейпереходов

.(7.1)

Если системанаходится в состоянии, в котором занято k (1 ≤ k ≤ n) каналов, то переход ее в левое соседнее состояние порождается потоком, представляющим собой суммуkпотоков обслуживаний. Поэтому интенсивность этого суммарного потока будет равна kμ.Таким образом,   плотности вероятности переходов СМО по стрелкам справа налево

 =       

.(7.2)                                                                                                                                                   

Из графа состояний видно, что процесс, протекающий в СМО, является процессом гибели и размножения с конечным числом состояний. Поэтому со временем установится предель­ный режим его протекания, и существуют предельные вероят­ности состояний p_k, k = 0,1,…,n+m, которые можно найти из формул (3.19)-(3.21), заменяя в них nна n+m и подставляя (7.1) и (7.2).

Для k = 1,…,n подставим формулы (7.1) и (7.2) в формулу (3.21), используя показатель нагрузки ρ = λ/ μ, получим:

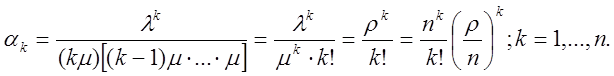
Для k = n+1 из формул (3.21), (7.1) и (7.2) будем иметь:

.

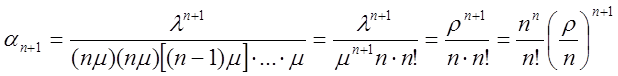Аналогично

.

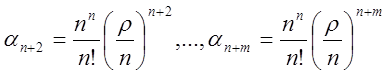Итак,

                   

       

                       .

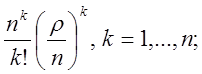
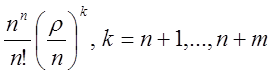Введем в рассмотрение величину ψ = ρ/n, представляющую собой показатель нагрузки, приходящийся на один канал, получим

=     (7.3)

Тогда из выражения (3.19):

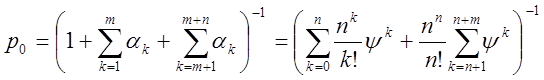.                  (7.4)

Вторая сумма в правой части равенства (7.4) есть сумма m членов геометрической прогрессии с первым членом  ψⁿ⁺¹ и знаменателем ψ. Если ψ ≠ 1, то по формуле суммы m  членов геометрической прогрессии

.

Если же ψ = 1, то .

Таким образом, (7.4) примет вид

;

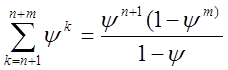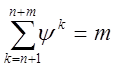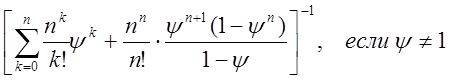p₀ = 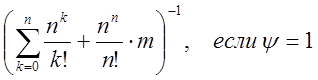                 .(7.5)

Теперь мы можем найти и остальные предельные вероятности состояний, подставив равенство (7.3) в формулу (3.20):

                                          

p_k =

                ,   (7.6)

где ρ₀ определяется по формуле (7.5).

Используя найденные предельные вероятности состояний, выведем формулы для некоторых характеристик эффективности функционирования рассматриваемой СМО.

Заявка, поступившая в момент, когда заняты все nканалов и все m мест в очереди, т.е. когда СМО находится в состоянии s_n+m получает отказ. Поэтому вероятность отказа есть вероят­ность того, что СМО находится в состоянии s_n+m.Следователь­но, из равенства (7.6) при k=n+m  получаем:

                                              .                                        (7.7)

Поскольку события отказа заявке и приема ее в СМО явля­ются противоположными, то вероятность принятия в систему пришедшей заявки

.(7.8)

Относительная пропускная способность Q совпадает с веро­ятностью p_сис:

.(7.9)

Тогда абсолютная пропускная способность:

.

Выведем формулу для среднего числа занятых каналов, или что то же, для среднего числа  заявок, находящихся под обслуживанием. Так как каждый занятый канал обслуживает в среднем μ заявок в единицу времени, а вся система обслуживает в среднем А заявок в единицу времени, то

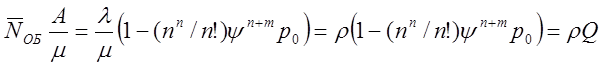.(7.10)

Для вычисления среднего числа заявок, находящихся в очереди,  рассмотрим дискретную случайную величину N_ОЧ – число заявок в очереди.

Очевидно, что закон распределения этой случайной величины будет иметь вид:

NОЧ	0	1	2	…	m
P	p	pn+1	pn+2	…	pn+m

Здесь p = p₀ + p₁ +…+ p_n. Поясним, что случайная величи­на N_ОЧ принимает значение 0 с вероятностью p, равной сумме вероятностей p₀ + p₁ +…+ p_n, поскольку событие, состоящее в том, что в очереди нет ни одной заявки, является объединени­ем событий, состоящих в том, что СМО находится в каждом из состояний s₀, s₁, …, s_n. Исходя из этого закона распределения, среднее число подсчитаем как математическое ожидание случайной величины N_ОЧ, используя формулы (7.6):

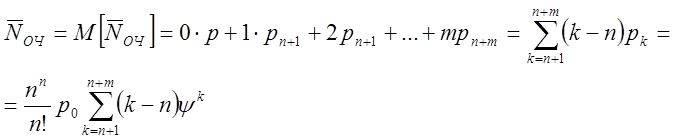(7.11)

В сумме правой части этого равенства произведем замену индекса суммирования:

l = k-n. Тогда k =l+n, l =1 при k = n+1 и l=m при k = n+m. В результате получим:

.

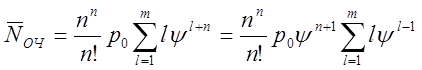Пользуясь формулой (5.12) при замене в ней ρ на ψ ≠ 1 и формулой суммы m членов арифметической прогрессии 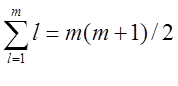, найдем для  окончательное выражение:

;

                      =

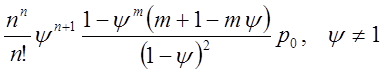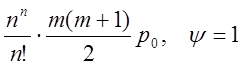                                              .                                                          (7.12)

Зная среднее число  заявок, находившихся под обслуживанием, и среднее число заявок, стоящих в очереди, можно найти среднее число заявок, находящихся в системе:

.                                                               (7.13)

Теперь подсчитаем среднее время ожидания заявки в очереди. Рассмотрим n+m+1 несовместных гипотез H_k, k=0,1,…,n+m, состоящих в том, что СМО находится соответственно в состоянии s_k, k=0,1,…,n+m. Тогда вероятности этих гипотез  p(H_k) = p_k, k=0,1,…,n+m.