Многоканальная СМО с ожиданием и ограничением на длину очереди, страница 2

Если заявка поступит в СМО при одной из гипотез  H_k, k=0,1,…, n-1, т.е. когда СМО находится в одном из состояний s_k, k=0,1,…, n-1, в каждом из которых не все каналы заняты, то она немедленно попадает под обслуживание свободного канала и ей не придется стоять в очереди. Поэтому условное математическое ожидание М[Т_ОЧ | H_k] случайной величины Т_ОЧ – времени ожидания заявки в очереди при гипотезах H_k, k=0,1,…, n-1, представляющее собой среднее время ожидания в очереди заявки, поступившей в СМО в момент, когда последняя находилась в состоянии  s_k, k=0,1,…, n-1, равно нулю: М[Т_ОЧ | H_k] = 0, k=0,1,…, n-1.

 Если заявка поступит в систему при гипотезе H_n, т.е. когда СМО находится в состоянии s_n,  в котором все n каналов заняты, но очереди нет, то заявке придется ждать освобождения одного из n каналов, которое произойдет под воздействием суммарного потока, слагающегося из  n потоков обслуживаний, каждый из которых имеет интенсивность μ. Поэтому интенсивность этого суммарного потока будет равна nμ, а условное математическое ожидание М[Т_ОЧ | H_n] случайной величины Т_ОЧ при гипотезе H_n, совпадающее со средним временем ожидания в очереди заявки, поступившей в СМО, когда последняя находилась в состоянии s_n, равно 1/(nμ), т.е. М[Т_ОЧ | H_n] = 1/( nμ).

Если заявка поступит в СМО при гипотезе H_n+1,т.е. когда система пребывает в состоянии s_n+1,в котором все п каналов заняты и в очереди одна заявка, то поступившей заявке при­дется в очереди, в среднем ждать время, равное 2/( nμ), складывающееся из среднего времени  1/( nμ) освобождения одного из каналов, под обслуживание которого попадает заявка, стоящая в очереди впереди, и среднего времени 1/( nμ) следующего освобождения одного из каналов. Поэтому М[Т_ОЧ | H_n+1] = 2/( nμ).

И так далее. Если заявка поступит в систему при гипотезе H_n+m-1,то М[Т_ОЧ | H_n+m-1] = =m/( nμ).

Наконец, если заявка поступит в СМО при гипотезе H_n+m, т.е. когда система находится в состоянии s_n+m, в котором  все n каналов заняты и в очереди стоят т заявок, то она получает отказ и покидает систему. Следовательно, М[Т_ОЧ | H_n+m] = 0.

Таким образом, по формуле полного математического ожи­дания ([9], с. 77)

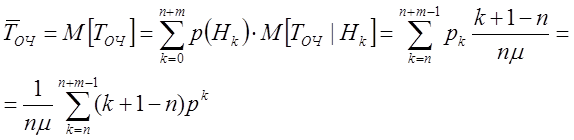
Подставим сюда выражение вероятностей состояний p_k по формулам (7.6), получим:

.

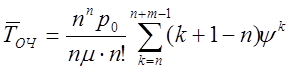Сделав в сумме справа замену индекса суммирования l = k+1 и затем заменив l на k, будем иметь:

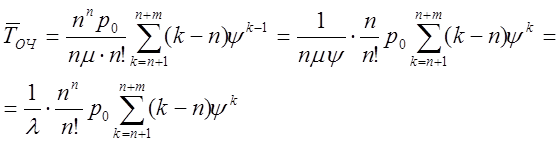
Но тогда по формуле (7.11):

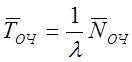                            .                                                                (7.14)

Таким образом, как и в случае одноканальной СМО с ожиданием и с ограничением на длину очереди, получим формулу Литтла, показывающую, что среднее время ожидания заявки в очереди  прямо пропорционально среднему числу заявок в очереди  с коэффициентом 1/ λ.

Подставим равенство (7.12) в формулу (7.14), можно получить другое выражение для :

;

                       =     .

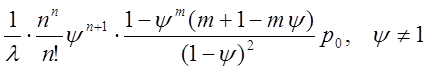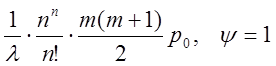Аналогично тому, как это было сделано в разделе 5 для одноканальной СМО, можно вывести выражение для среднего времени пребывания заявки в системе (см. формулу (5. 26)):

 ,                                                       (7.15)

где  - среднее время обслуживания одной заявки, относя­щееся ко всем заявкам – обслуженным и «отказникам»:

,

откуда с учетом (7.10) получаем формулу Литтла:

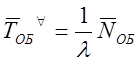.                                                                (7.16)

 Подставим равенства (7.14) и (7.16) в формулу (7.15) и с учетом формулы (7.13) получим еще одну формулу Литтла:

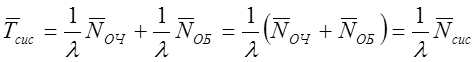,                  (7.17)

связывающую среднее время пребывания заявки в системе  со средним числом заявок в системе .

Нетрудно убедиться в том, что при п = 1 формулы (7.5) и (7.6) превращаются в формулы (5.5) соответственно для р₀ и р_k, (k= 1, .., т+1), а формулы (7.7), (7.8),(7.9), (7.10), (7.12), (7.13), (7.14), (7.16) и (7.17)- соответственно в формулы (5.7), (5.8), (5.9), (5.19), (5.17), (5.20), (5.23), (5.25) и (5.27) для одноканальной СМО с ожиданием и ограничением на длину очереди.

Сведем параметры и полученные характеристики функцио­нирования рассмотренной СМО в табл. 7.1 и 7.2.

Таблица 7.1

Параметры многоканальной СМО с ожиданием

 и ограничением на длину очереди

№ п/п	Параметры	Обозначения, значения
1	Число каналов обслуживания	n ≥ 1
2	Интенсивность входящего простей­шего потока заявок ПВХ.	in Пвх = λ = const (λ не зависит от времени t)
3	Производительность каждого кана­ла -интенсивность простейшего потока «обслуживании» ПОБ каждым каналом (среднее число заявок, об­служиваемых одним каналом за еди­ницу времени при непрерывной его работе)	in Поб = μ = const (μ не зависит от времени t)
4	Максимальная длина очереди -максимальное число мест в очереди	m ≥ 1

Таблица 7.2

Характеристики функционирования многоканальной

СМО с ожиданием и ограничением на длину очереди

№ п/п	Предельные характеристики	Обозначения, формулы
1	Показатель (коэффициент) на­грузки СМО (трафик)
2	Показатель (коэф­фициент) нагрузки, приходящейся на один канал
3	Вероятность того, что все каналы сво­бодны     (вероятность простаивания всей системы)	;  p0 =
4	Вероятность состоя­ний	, pk  =
5	Вероятность отказа заявке
6	Вероятность того, что заявка будет принята в СМО
7	Относительная пропускная способность СМО
8	Абсолютная пропускная способность СМО
9	Среднее число занятых каналов (т.е. среднее число заявок, находящихся под обслуживанием)
10	Среднее число заявок, находящихся в очереди	;  =
11	Среднее число заявок, находящихся в СМО (как в очереди, так и под обслуживанием)
12	Среднее время ожидания заявки
13	Среднее время пребывания заявки в очереди
14	Среднее время обслуживания одной заявки, относящееся ко всем заявкам – как обслуженным, так и получившим отказ