Элементы теории систем управления

2. Элементы теории систем управления.

2.1. Понятие переходных и установившихся процессов системы, устойчивость и ОС.

После структуризации системы и установления структур целей и функций элементов системы, возможно обратиться к процессу функционирования каждого элемента системы.

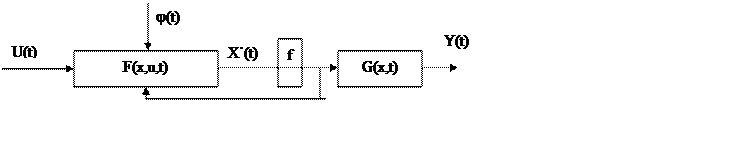Выше было определено понятие «состояние» объекта управления как некоторый «срез» поведения его во времени, это внутренние перемены ОУ, некоторый вектор Х, который и будем рассматривать как вектор переменных состояния. Выходной вектор переменных Y в общем случае является функцией вектора Х:  G(X, t); t означает, что на объект действуют внешние или внутренние возмущения или параметры функции G(X, t) зависят от времени. На вход объекта поступают управляющие воздействия -  вектор U(t) и возмущения j(t). В результате структура ОУ примет вид:

Рис. 2.1.

X˙= F(x,u,t)

Y = G(x,t)

Управление – это процесс воздействия на ОУ для выполнения поставленной цели.

Рассмотрим  i-ый элемент вектора состояния x_i(t). Пусть он находился в некотором начальном состоянии x⁰_i(t) (Рис. 2.2)

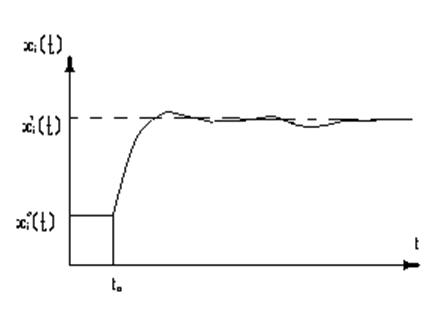
Рис. 2.2.

В момент времени t₀ на систему подействовало управляющее или возмущающее воздействие. В результате ОУ перешел из состояния x⁰_i(t) в состояние x¹_i(t). Этот переход объекта из одного состояния в другое и называется переходным процессом, это динамика ОУ. После завершения в ОУ переходного процесса в нем устанавливается новое состояние равновесия x¹_i(t). Это состояние называется установившимся процессом или статикой объекта.

Переходный процесс, показанный на рисунке 2.2, является устойчивым. Под устойчивостью будем понимать способность ОУ возвращаться в состояние равновесия (может быть не первоначальное) после действия на него управляющего или возмущающего воздействия. Обычно в результате действия на систему управления U(t) состояние равновесия будет новым, как показано на рисунке 2.2. Если же на объект действует возмущение (вредное воздействие j(t)), то требуется с помощью правильных управленческих решений вернуть объект в исходное состояние равновесия. (рис 2.3)

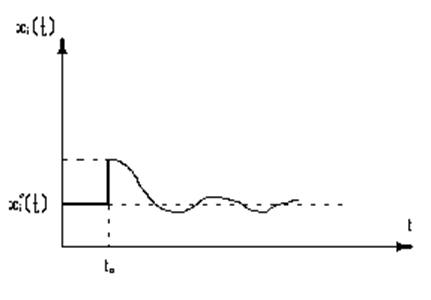
Рис. 2.3

Основополагающим принципом управления является принцип обратной связи (ОС), который показан на рис 2.4.

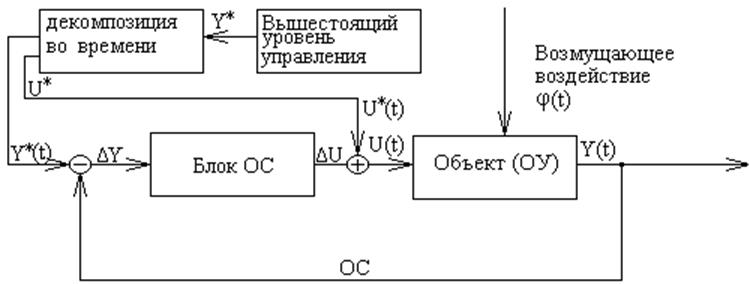
Y^*(t) – задающее воздействие, желаемое поведение Y(t)

Рис. 2.4.

Желаемое поведение ОУ Y^*, формируется вышестоящей системой управления (СУ). Задачей управляющей системы данного уровня иерархии является определение X^*(t), и соответствующего ему U^*(t), в блоке ОС определяется, ΔY(t)=Y^*(t)-Y(t), и на основе этого рассогласования выработать меры воздействия на процесс функционирования ОУ такие, чтобы ΔY(t)=0. Для этого и служат ОС.

2.2. Управляемость, наблюдаемость, достижимость.

Под управляемостью системы нижележащего уровня понимается ее способность выполнять цели и функции, устанавливаемые системой вышестоящего уровня, в противном случае система нижележащего уровня является неуправляемой по всем или части переменных состояний. Это требует пересмотра ее структуры или полагаемых целей и функций.

Если систему нижележащего уровня (объект управления) удается формализовать в виде системы линейных ОДУ, то факт управляемости (или неуправляемости) ОУ можно установить аналитически. Пусть имеем систему ОДУ вида:

Х=Ах+Bu,  (2.1.)

Где Х – вектор переменных состояний, dim X=n,

       U – вектор управляющих переменных, dim U=m;

       А и В – постоянные матрицы, dim А=n*n, dim B=n*m.

Теорема 3.1. Критерии управляемости. Линейная стационарная система (2.1.), управляема тогда и только тогда, когда

Rank U=rank[ B, AB,…, A^n-1B]=n (2.2.)

V – матрица управляемости.

Если условие (2.2.) не выполняется, то управление U может влиять не на все переменные состояния ОУ. В этом случае возникает необходимость выделения управляемых и неуправляемыз переменных. Приведем алгоритм решения задачи. Пусть rank U=r. Это означает, что матрица управляемости имеет только r линейно независимых столбцов e₁, e_2,…,e_r. Сформируем матрицу Т по правилу: T=(T_1, T₂), dim T=n*n,

Где T₁=(e₁,…,e_r), T₂=(e_r+1,…,e_n).

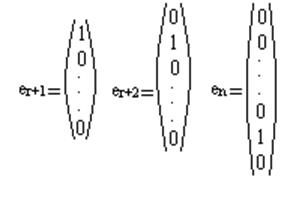
Здесь e_r+1,…,e_n – любые (n-r) независимых столбцов

Их можно выбрать, например, в виде:

Обсудим понятие наблюдаемости. Если система нижележащего уровня является «прозрачной» для системы вышестоящего уровня, т.е. эта система может «видеть» значения переменных состояния Х, то нижележащая система является наблюдаемой.

Все векторы l_i, i = 1,n должны составлять систему из n линейно-независимых векторов, т. е.

            Сформулируем матрицу:

,

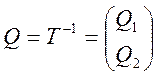где матрица Q₁ имеет r строк, а матрица Q₂ имеет (n-r) строк. Вводя преобразование координат , из системы (2.1) получим:

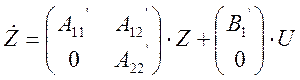
где ,  ,  , 

(2.3 а)

В развернутой форме:

(2.3 б)

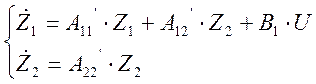
где , 

            Из системы (2.3) видно, что подсистема (2.3 б) изменяется во времени в силу собственных свойств матрицы  и не зависит от управления U.

Аналитически наблюдаемость можно установить, если известна модель объекта управления (ОУ) в виде:

(2.4)

,  .

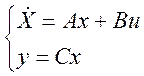
Теорема 2.2.  Критерий наблюдаемости. Объект управления (2.4) является наблюдаемым тогда и только тогда, когда

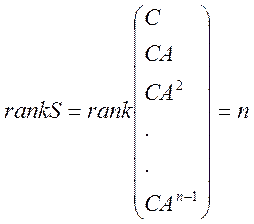
            Если rank S<n, то часть переменных Х является ненаблюдаемой. Имеется процедура, позволяющая выявить наблюдаемые и ненаблюдаемые переменные Х.

Достижимость.   Состояние системы Х₁ называется достижимым из состояния Х₀, если существует такое состояние U(t), которое способно перевести систему из состояния Х₀ в состояние Х₁.

Критерий достижимости тот же, что и критерий управляемости. Эти понятия эквивалентны.

2.3.  Элементы теории адаптивных систем

Любая сложная система работает не автономно, а в условиях действия агрессивной внешней среды, то есть такой среды, которая действует на сложную систему в направлении, изменяющем её поведение в сторону отклонений от требуемых значений выходных переменных. При этом характеристики сложной системы могут меняться заранее непредвиденным образом. Поэтому необходимо в структуре управления иметь управляющую подсистему, которая будет адаптировать поведение объекта к действиям внешней среды таким образом, чтобы поведение системы оставалось неизменным и соответствовало желаемому. При этом может меняться структура и параметры системы управления.