Структура адаптивной системы может быть представлена в виде рис. 2.5.6

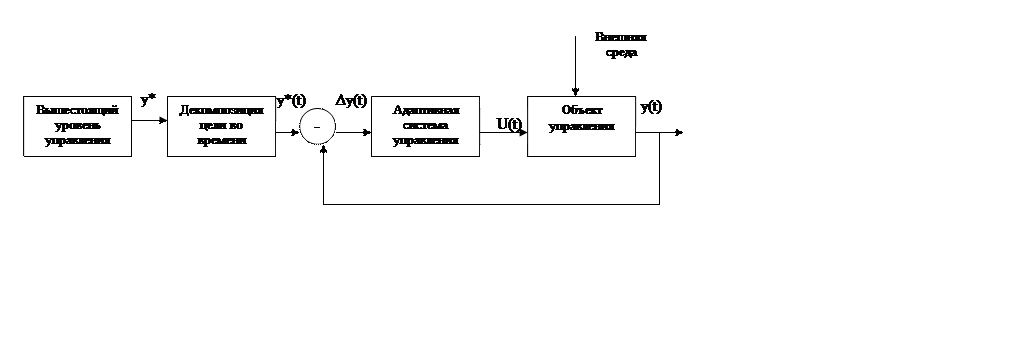
Рис. 2.5.
Здесь y* - цель функционирования подсистемы данного уровня (объекта управления) на заданный период времени;
y*(t) – декомпозиция цели y* во времени;
Δy(t) – отклонения действительного значения y(t) от заданного y*(t);
Функциональная схема адаптивной системы с эталонной моделью представлена на рисунке 2.6
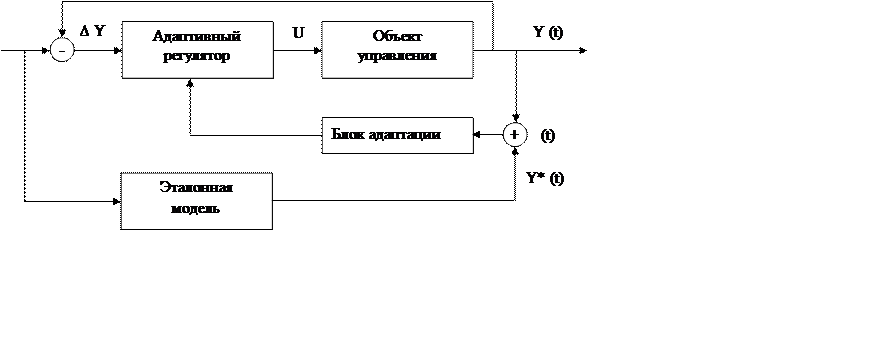
Рисунок 2.6.
Эталонная модель отражает требования к поведению замкнутой системы. Когда выходы ОУ и эталонной модели совпадают, ∆ = 0 и адаптивный регулятор не работает.
 Если выход ОУ
отличается от эталонного то по алгоритму, заложенному в блоке адаптации,
происходит перестройка параметров адаптивного регулятора так, чтобы поведение
всей системы соответствовало заданным требованиям.
Если выход ОУ
отличается от эталонного то по алгоритму, заложенному в блоке адаптации,
происходит перестройка параметров адаптивного регулятора так, чтобы поведение
всей системы соответствовало заданным требованиям.
Основные понятия
В промышленности существует класс объектов и технологических процессов, характеристики которых во времени могут изменяться заранее непредвиденным образом, например химические реакторы, некоторые виды металлургических процессов, процессы обогащения, ряд тепловых процессов и т. д. На. все, системы управления оказывает влияние окружающая среда. Необходимость решения задач, требующих изменения управления при изменении условий работы, вызвала появление и развитие адаптивных систем.
Адаптивными называют такие системы управления, в которых
структура и (или) параметры системы управления изменяются вслед за изменяющимися параметрами объекта управления так, чтобы поведение замкнутой системы оставалось неизменным и соответствовало желаемому. Выделяют два следующих основных класса адаптивных систем.
· Адаптивные системы с эталонной моделью (АСЭМ).
· Адаптивные системы с идентификатором (АСИ).
Адаптивная система с идентификатором (АСИ)
Адаптивная система с идентификатором работоспособна при достаточно медленном по сравнению с темпом переходных процессов изменении параметров объекта. На рис2$- показана ее функциональная схема.

|
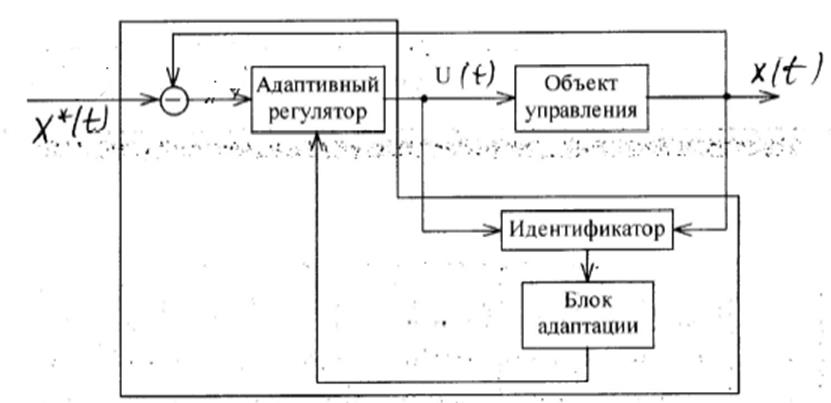
Рис. 2.7 Функциональная схема адаптивной системы с идентификатором
Идентификатор предназначен для оценивания в каждый текущий момент времени изменяющихся параметров объекта. На основе этой информации по алгоритму, заложенному в блоке адаптации, изменяются параметры регулятора таким образом, чтобы динамика системы оставалась неизменной.
При неизменных параметрах объекта параметры регулятора также остаются неизменными, т.е. АСИ в этом случае работает как обыкновенная система стабилизации.
Рассмотрим идею идентификации параметров и алгоритма адаптации на примере объекта 1-го порядка.
![]()
![]() (2.5)
(2.5)
где ![]() и
и ![]() неизвестные коэффициенты объекта.
Они изменяются на порядок медленнее скорости переходных процессов.
неизвестные коэффициенты объекта.
Они изменяются на порядок медленнее скорости переходных процессов.
Вход и выход объекта измеряются, дискретно, причем шаг дискретизации на порядок меньше времени перехода процесса объекта. Из измеренных значений в идентификаторе «формируется» система уравнений

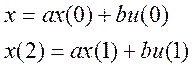 (2.6)
(2.6)
Берется столько отсчетов, сколько параметров нужно определить. Система преобразуется к виду
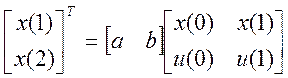 (2.7)
(2.7)
Проверяется условие 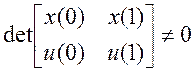 .
Если оно выполняется, то определяются неизвестные параметры в виде:
.
Если оно выполняется, то определяются неизвестные параметры в виде:
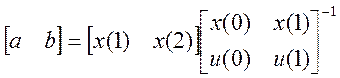
Для текущей идентификации параметров в системе 2.6
«отбрасывается» первое уравнение и добавляется следующее, которое содержит
измеренные значения ![]() и
и ![]() .
Вновь решается сформированная система уравнений 2.7 и т.д. Если на каком-то шаге получается вырожденная матрица
измеренных значений
.
Вновь решается сформированная система уравнений 2.7 и т.д. Если на каком-то шаге получается вырожденная матрица
измеренных значений 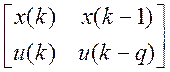 , то в качестве параметров
объекта принимаются предыдущие значения
, то в качестве параметров
объекта принимаются предыдущие значения ![]() и
и
![]() .
.
Алгоритм адаптации
Для объекта (2.5) выбирается закон управления
![]()
где ![]() и
и ![]() - перестраиваемые коэффициенты
регулятора. Определяется уравнение замкнутой системы:
- перестраиваемые коэффициенты
регулятора. Определяется уравнение замкнутой системы:
![]()
 На основе требований к качеству процессов в замкнутой
системе формируется желаемое дифференциальное уравнение:
На основе требований к качеству процессов в замкнутой
системе формируется желаемое дифференциальное уравнение:
![]()
Приравниваются правые части уравнений (2.9) и (2.10)
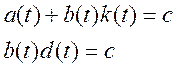 (2.9
- 2.10)
(2.9
- 2.10)
Отсюда определяется закон изменения параметров адаптивного регулятора:
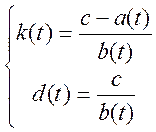 (2.11)
(2.11)
Эту процедуру можно распространить на объекты более высокого порядка!
Таким образом, адаптивный регулятор работает по алгоритму (2.8). В блоке адаптации вычисляется параметры регулятора, законы изменения этих параметров по алгоритму (2.11).
Пример экономической модели первого порядка.
Введем значения:
![]() – национальный доход;
– национальный доход;
![]() – накопление основных производственных фондов;
– накопление основных производственных фондов;
![]() - потребление
(непроизводственное потребление, непроизводственное накопление, прирост материальных
оборотных средств, государственных материальных резервов, потери).
- потребление
(непроизводственное потребление, непроизводственное накопление, прирост материальных
оборотных средств, государственных материальных резервов, потери).
![]() (2.12)
(2.12)
 Наиболее простая модель воспроизводства национального
дохода с использованием (2.12) формируется на основе двух основных допущений:
Наиболее простая модель воспроизводства национального
дохода с использованием (2.12) формируется на основе двух основных допущений:
·
пропорциональности производственного накопления
![]() и прироста национального дохода в
тот же момент времени, т.е. величине
и прироста национального дохода в
тот же момент времени, т.е. величине ![]()
·
независимости динамики потребления ![]() . Тогда из управления (2.12),
получим:
. Тогда из управления (2.12),
получим:
![]() (2.13)
(2.13)
где ![]() – капиталоемкость
национального дохода (отношение производимого накопления к приросту
национального дохода). Очевидно, что параметр
– капиталоемкость
национального дохода (отношение производимого накопления к приросту
национального дохода). Очевидно, что параметр ![]() может
меняться во времени
может
меняться во времени ![]() .
.
Управляющим воздействием здесь может быть потребление ![]() за счет изменения в нужном
направлении. Из уравнения (2.13) можно получить
за счет изменения в нужном
направлении. Из уравнения (2.13) можно получить ![]() в
явном виде:
в
явном виде:
![]() (2.14)
(2.14)
Если рассматривать хозяйство страны в разрезе n отраслей, то
получим систему линейных дифференциальных уравнений ![]() -го
порядка.
-го
порядка.
![]()
А.Г. Гранберг. Динамические модели народного хозяйства. Учебное пособие. – М: Экономика, 1985.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.