Между частицами, составляющими твердые тела, действуют как силы притяжения, так и силы отталкивания. Об этом свидетельствует очевидный факт: все твердые тела сопротивляются как деформации растяжения, так и деформации сжатия, причем сопротивление деформации сжатия, как правило, выше. При каком-то, характерном для данных условий воздействия межатомном расстоянии, эти силы уравновешивают друг друга. Иногда таких равновесных расстояний может быть несколько.
Поставим себе задачу: как описать это противоречивое взаимодействие, пока безотносительно как к внутреннему строению конденсата, так и строению атомов и молекул, его составляющих.
Из ряда фундаментальных сил природы - гравитационное, электромагнитное, сильное и слабое - лишь электромагнитное взаимодействие способно обеспечить силы, достаточные для обеспечения межатомных и межмолекулярных сил, жестких и пластичных одновременно. Теория и опыт показывают:
1) силы притяжения между частицами твердого тела проявляются уже при таких расстояниях, при которых силы отталкивания еще не сказываются;
2) те и другие силы возрастают с уменьшением расстояния между частицами, но силы отталкивания возрастают значительно быстрее, чем силы притяжения;
3) в конечном итоге силы взаимодействия имеют электростатическую природу и поэтому силы притяжения отрицательны, как обеспечиваемые взаимодействием зарядов противоположного знака, а силы отталкивания - положительны.
Схематически в рамках двухатомной модели силы взаимодействия представлены на рис. 1.2.1.
В самом общем виде величины сил можно представить так:
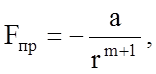
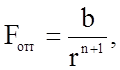
где r - расстояние между частицами (порядка 0,2 - 1 нм),
a,b - константы для данной взаимодействующей пары,
m,n - константы, зависящие от физической природы сил притяжения и отталкивания соответственно, причем n>m.
Результирующую силу опишет выражение
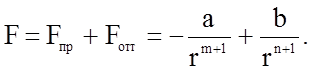(1.2.1)
Очевидно, должно существовать такое r=d0, при котором F=0, что соответствует равновесным условиям.
 |
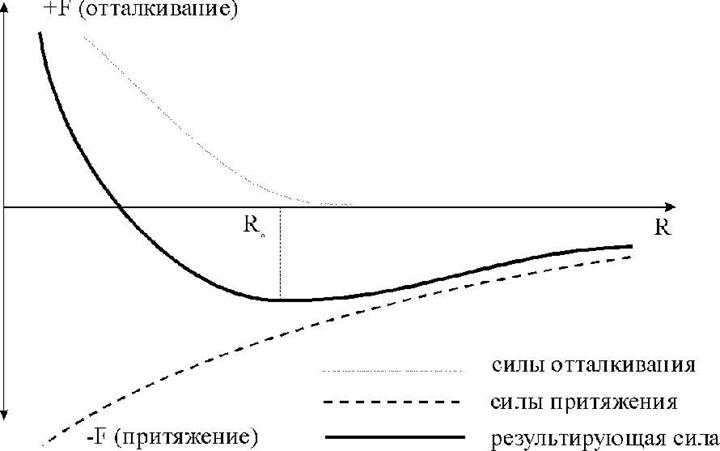Рис.1.2.1. Силы взаимодействия между двумя атомами
Из курса механики известно, что F = - grad U = -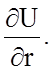 
Легко показать, что уравнение (1.2.1) может быть получено дифференцированием выражения:
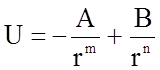, (1.2.2)
которое называется потенциалом
Г.А. Ми и выражает потенциальную энергию взаимодействия двух частиц. Здесь введены новые константы
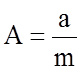и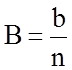 
.
На рис. 1.2.2 представлены графически в условном масштабе кривые, описываемые уравнениями (1.2.1) и (1.2.2). Из рис. (1.2.2) следует, что F(r) и U(r) имеют асимптотические значения:
U(r) Þ0 и F(r) Þ0, при гÞ¥ и U Þ+¥ и F(r)Þ¥, при гÞ0. Минимум U(r) = U0(d0) отражает максимальную энергию связи, а минимум F(г) = F(d1) соответствует максимальному усилию, которое может выдержать рассматриваемая модель по отношению к силам растяжения.
 |
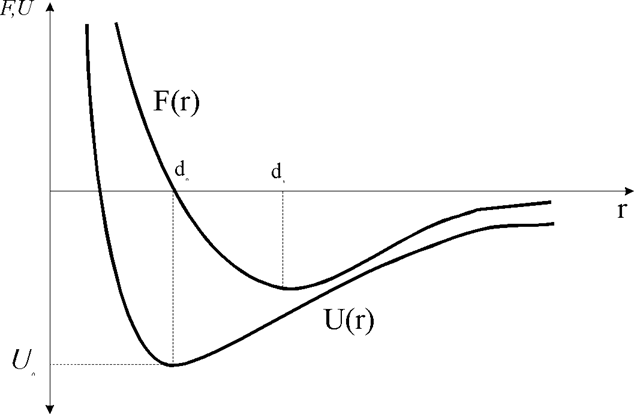Рис.1.2.2. Зависимость силы и потенциальной энергии взаимодействия двух частиц от расстояния между ними
При описании строения и свойств реальных конденсированных материалов приходится учитывать, что любое тело представляет собой объединение многих взаимодействующих частиц, причем их объединение может происходить различными путями.
В объединении атомов в процессе возникновения конденсированного состояния решающую роль играет строение внешних незамкнутых и замкнутых электронных оболочек.
В зависимости от характера перестройки электронных оболочек, сопровождающей выстраивание атомов в теле кристаллического и аморфного строения, различают 5 типов межатомных связей: ионную, молекулярную, ковалентную и водородную. В реальных твердых телах в чистом виде эти связи встречаются редко, как правило, в однокомпонентных системах. Практически в многокомпонентных системах всегда имеет место сосуществование двух или более типов связи, однако чаще всего одна из них имеет превалирующее значение, определяя структуру и свойства тела. Под многокомпонентными системами будем понимать вещества, состоящие из различных атомов, а также многофазные или гетерогенные по строению, например, состоящие частично из аморфной фазы, а частично - из кристаллов.
При анализе устойчивости того или иного состояния общепринятой количественной характеристикой является энергия связи: это энергия, которую нужно сообщить одному молю вещества (обычно в виде теплоты), чтобы разложить его на отдельные невзаимодействующие атомы или молекулы. Теоретическое вычисление этой энергии - трудная, а в ряде случаев нерешенная до сегодняшнего дня задача, поскольку точные квантово-механические решения для взаимодействия частиц числом более трех пока не получены из-за чрезвычайной математической сложности.
В области производства керамики и стекла, многие материалы являются ионными кристаллами или веществами со смешанным типом связи - ковалентными и ионными. Связность сырья, например, руды, глины, определяется молекулярными силами сцепления. Значительно реже в этой отрасли технолог имеет дело с материалом, характеризующимся металлическим типом связи (например, при производстве высокоэлектропроводной керамики или металлических стекол).
В реальном конденсате атом и молекула взаимодействуют с несколькими соседями. Ближайшие соседи, находящиеся на одинаковых расстояниях в эквивалентных положениях, образуют первую координационную сферу. Число таких соседей называется координационным числом Z и составляет в наиболее распространенных типах решеток от 3 до 12. Воздействие любого выделенного атома практически не распространяется далее второй координационной сферы - далее второго атомного слоя, окружающего данный атом (молекулу).
Учет взаимодействия с соседними частицами требует введения в уравнение (1.2.2) для потенциалов дополнительных членов, а также коэффициентов, зависящих от электронного строения и электронного обмена взаимодействующих атомов. Кроме того, увеличение температуры сопровождается ростом кинетической энергии колебаний узлов решетки, что также требует учета при количественной оценке энергии связи.
При описании веществ с ионным типом связи достаточную точность можно достигнуть, используя уравнение для потенциальной энергии, предложенное Маделунгом
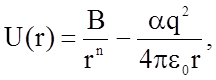(1.2.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
