где a -
константа Маделунга, q, - заряд взаимодействующих ионов, e0= 8,85×10-12 Ф/м - электрическая постоянная. Очевидно, что в этом случае в уравнении
(1.2.2) величина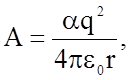 
а m=1; параметр n зависит от вида взаимодействующих атомов и равен
примерно 9... 10, кроме солей лития, для которых n = 5.
При неквантовом описании ионной связи часто применяется также потенциал Борна и Майера:
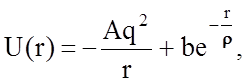(1.2.4)
где А - константа, по смыслу совпадающая с константой Маделунга, b и r - константы, определяемые опытным путем. Для многих галогенидов щелочных металлов r=0,3Å . Следует отметить, что второй член потенциала Борна-Майера, включающий экспоненту, в ряде случаев более точно описывает энергию отталкивания, чем степенная функция выражений (1.2.2) и (1.2.3).
Слабые молекулярные силы Ван-дер-Ваальса описываются с помощью потенциала Леннарда-Джонса
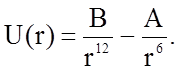(1.2.5)
Часто используют удобную безразмерную форму записи уравнения (1.2.5):
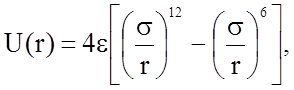
т.е. применяется замена: 4es6=A; 4es12=B.
Более точное описание требует учета кинетической энергии, которая может вносить вклад более 10%.
Значительно сложнее получить сколько-нибудь надежные количественные оценки при расчете устойчивости твердых тел, образованных за счет ковалентных и металлических межатомных связей. В этих случаях необходимо использовать квантово-механические представления о строении атомов и их взаимодействии.
Так, ковалентная связь обусловлена обменным взаимодействием внешних "неспаренных" электронов, имеющих антипаралельные спины.
 |
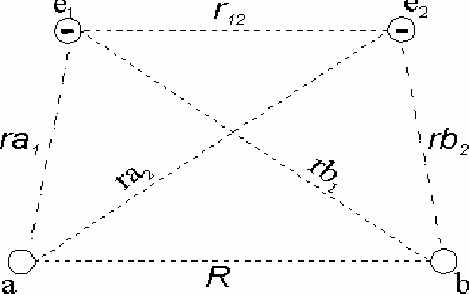В простейшем примере ковалентной связи в молекуле водорода рассмотри общие принципы подхода к решению таких квантовомеханических задач. Мы должны вычислить энергию взаимодействия двух атомов водорода, протоны которых a и b находятся на любом расстоянии R друг от друга (рис.1.2.3). Запишем уравнение Шредингера для двух электронов, движущихся в молекуле водорода
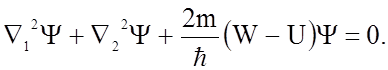(1.2.6)
Здесь D12Y и D22Y - операторы Лапласа для волновых Y- функций электронов 1 и 2.
Потенциальная энергия U(r1,r2,R) молекулы слагается из нескольких частей: энергии притяжения электронов a и b к обоим ядрам, энергии отталкивания ядер a и b друг от друга, энергии взаимного отталкивания электронов.
В общем случае нужно записать
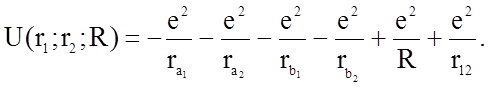(1.2.7)
Точное решение уравнения (1.2.6) даже в этом простейшем случае наталкивается на непреодолимые математические трудности, поэтому необходимо искать обходные пути, подбирая соответствующие приближения.
Гайтлер и Лондон (1927 г.) впервые объяснили строение молекулы водорода, применяя метод валентных схем, сущность которого заключается в использовании теории возмущений. Используя тот фундаментальный факт, что электроны неотличимы друг от друга, и, применяя в качестве приближения представление о том, что многоэлектронная волновая функция может быть получена из отдельных одноэлектронных функций, удается упростить выражение для потенциальной энергии (1.2.7) и получить решение уравнения (1.2.6). Имеющие в этом случае место кулоновское и обменное взаимодействия описываются соответствующими интегралами, причем на равновесных расстояниях обменный интеграл значительно превосходит кулоновский.
Установлено также, что параллельная ориентация электронных спинов приводит к отталкиванию атомов, а антипараллельная - к их притяжению. Таким образом, в молекуле водорода связь атомов обеспечивается движением пары электронов с противоположной ориентацией спинов в поле протонов - ядер молекулы (рис. 1.2.4).
 |
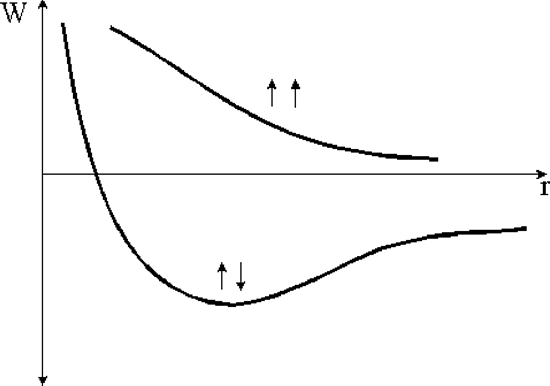Рис. 1.2.4. Энергия молекулы водорода в зависимости от ориентации спинов электронов и расстояния между атомами
При расчетах некоторых макроскопических характеристик веществ с таким типом связей, например, модулей упругости, электропроводности, значительных успехов можно достигнуть, применяя метод линейных комбинаций атомных орбиталей (ЛКАО). Основное предположение заключается в том, что при соединении атомов в молекулы или кристаллические группы состояния электронов в атомах, а, следовательно, описывающие их волновые функции изменяются не слишком радикально. Осуществляя линейные (в смысле - достаточно малые по величине перестройки) комбинации атомных волновых функций, можно отобразить качественные изменения, происшедшие в состоянии электронов в процессе объединения атомов в молекулы.
В результате следует признать, что подобно тому, как в атоме водорода электрон с различной вероятностью обнаруживается в различных точках пространства, так и в молекуле или в окрестности фиксированного атома решетки электрон "размазан" по пространству, но имеются предпочтительные направления, где он может быть обнаружен чаще всего. При рассмотрении достаточно ограничиться лишь анализом для валентных электронов, так как именно они и дают основной вклад в образование межатомных связей.
В настоящее время значительные успехи, как в качественном, так и количественном рассмотрении электронного строения молекул и атомных групп достигнуты с использованием метода ЛКАО - МО, метода, в котором одноэлектронная молекулярная орбиталь (МО) получается линейной комбинацией атомных орбиталей (ЛКАО).
Основой представлений о строении металла является модель, по которой обобществленное облако валентных электронов стягивает своим полем остовы атомов, объединенных в решетку.
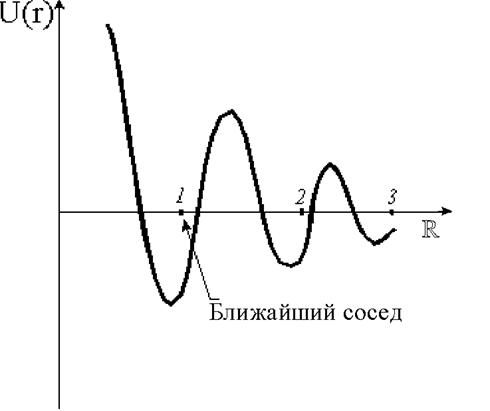
Рис. 1.2.5. Полный межатомный потенциал в металле
Расчет энергии связи при описании металлического конденсированного состояния - одна из наиболее трудных задач физики твердого тела. При решениях используют представления квантовой механики, в частности, метод псевдопотенциала. Установлено, что полную энергию сцепления металла можно разложить по потенциалу взаимодействия между валентными электронами и ионами. Этот потенциал и
заменяется псевдопотенциалом. В результирующей энергии взаимодействия выделяют слагаемое, соответствующее эффективному парному взаимодействию между ионами, это взаимодействие состоит из двух частей: прямого кулоновского взаимодействия (типа того, что определяло энергию кристалла по Маделунгу) и косвенного взаимодействия "ион-электрон-ион".
Потенциал взаимодействия в зависимости от расстояния до данного иона в металле схематически может быть представлен в виде осциллирующей функции (рис. 1.2.5).
В щелочных металлах осцилляции являются особенно дальнодействующими и простираются от каждого атома вплоть до его пятого соседа.
Рассмотрим известные типы межатомных связей более подробно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.