Теория и обработка сигналов MATLAB в ТОС, страница 8

» y=dimpulse(num,den,length(n));

» stem(n,y)

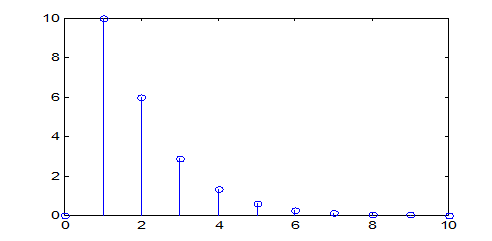
                               Рис.19.

» % диаграмма нулей и полюсов

» num=[10  0];  den=[1  -0.6  0.07];

» zplane(num,den);

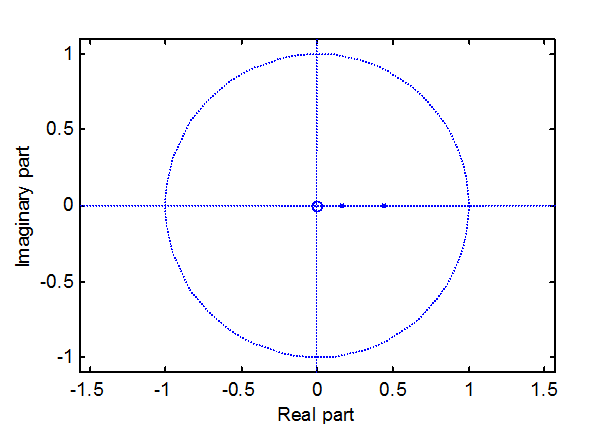
                               Рис.20.

Для вычисления выходного сигналаy линейной дискретной системы с переджаточной функцией 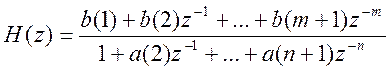при произвольном входном сигнале x может использоваться команда

y = filter(num, den, x, zi),

при этом ненулевые начальные условия задаются в векторе zi. Количество элементов в этом векторе определяется как  max(length(num),  length(den)-1).  В частности, для системы второго порядка с N = M =2 этот вектор равен
zi = [b₁*x[-1]+b₂*x[-2]-a₁*y[-1]-a₂*y[-2],  b₁*x[-1]-a₂*y[-1]]. 

            Пример использования функции filter для системы второго порядка с
num =[10   0],den=[1   -0.6   0.07], начальными условиями y[-1]=2,
 y[-2]=1 и входным сигналом в виде единичной последовательности

» n=0:10;  x=ones(1,11);

» num=[0  10];  den=[1  -0.6  0.07];

» zi=[0.6*2-0.07*1,  -0.07*2];

» y=filter(num, den, x, zi);

» stem(n, y), xlabel('n'), ylabel('y(n)')

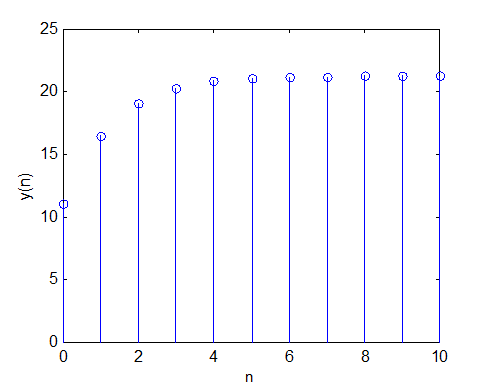
Рис.21.

Функция tf2zp() выполняет преобразование коэффициентов полиномов передаточной функции дискретной системы в нули и полюсы передаточной функции, функция zp2tf() осуществляет обратное преобразование.

Частотные характеристики дискретных систем

Расчет частотной характеристики  (H(e^jω)  дискретной системы выполняется с помощью одной из функций freqz(…).  Функция  freqz(a, b) вычисляет частотную характеристику и выводит в текущее графическое окно амплитудную частотную (АЧХ) и фазовую частотную (ФЧХ) характеристики.

Пример

» num=[10  0];  den=[1  -0.6  0.07];

» freqz(num,den)

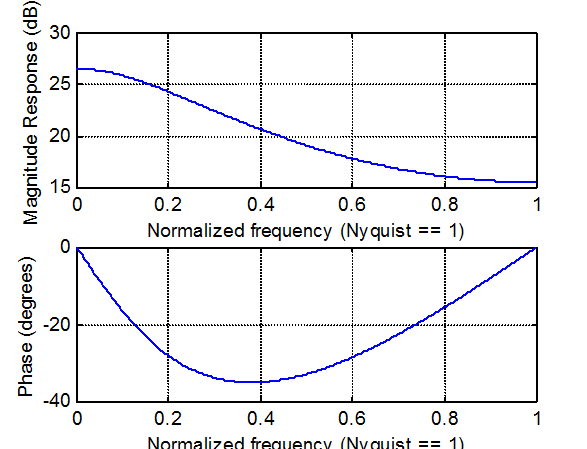
                               Рис.22.

            Функция  [h, f]=freqz(num, den, n, Fs) вычисляет n комплексных отсчетов частотной характеристики по векторам num, den при частоте дискретизации  Fs.  Возвращаемый параметр  f  содержит отсчеты частоты в герцах, равномерно распределенные в интервале от 0 до Fs/2,   количество элементов h и f равно n.

Пример

» figure(2)

» % логарифмический масштаб по оси частот, модуль АЧХ - в децибелах

» semilogx(f,20*log10(abs(h)))

» title('Амплитудно-частотная характеристика')

» ylabel('Модуль (дБ)'), xlabel('Частота, Гц'), grid

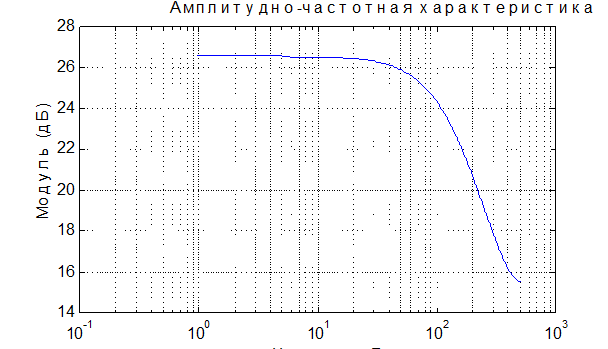
                                                        Рис.23.

Функция  [h,w]=freqz(b,a,w)     возвращает значения частотной характеристики для отсчетов частоты , заданных в векторе w.  При  этом отсчеты частоты должны задаваться в интервале от 0 до 2π.

Функция  Q = unwrap(P) корректирует фазо-частотную характеристику системы при переходе через значения  π,  устраняя разрывы функции.

Пример. Производится расчет фильтра нижних частот Чебышева 1 типа и строятся его частотные характеристики

Fs=1000; % Частота отсчетов

% Граничные частоты полосы пропускания и задерживания фильтра

Wp=200/500; Ws=240/500;

% Максимально допустимые пульсации

% в полосе пропускания и задерживания

Rp=1; Rs=30;

% Расчет порядка и передаточной функции ФНЧ

[n,Wn]=cheb1ord(Wp,Ws, Rp, Rs);

[b,a]=cheby1(n,Rp,Wn);

% Вычисление частотной характеристики

[h,f]=freqz(b,a,128,1000);

% Построение АЧХ

figure(1), subplot(3,1,1), plot(f, abs(h)), title(' АЧХ фильтра')

% Построение ФЧХ

subplot(3,1,2), plot(f, angle(h)), title('ФЧХ фильтра')

% Построение  скоректированой ФЧХ

subplot(3,1,3), plot(f, unwrap(angle(h))), xlabel('Частота, Гц')

           

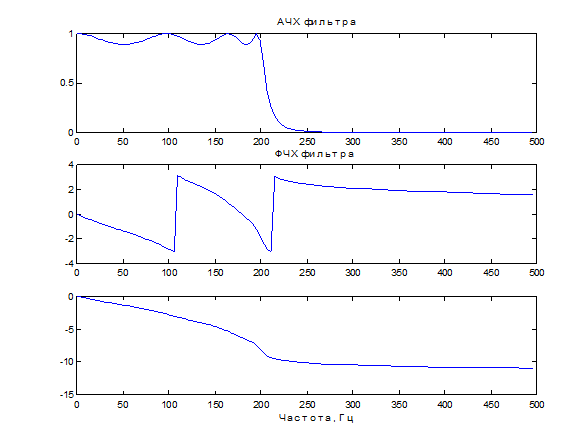
                                                                                                     Рис.24.

Передаточная функция и частотная характеристика  линейной дискретной системы  часто выражается через нули и полюса. Их принято представлять на комплексной плоскости. Для этого используют функции  zplane(z,p)  и  zplane(b,a).

Пример.

[b,a]=butter(11,0.3);

 zplane(b,a)

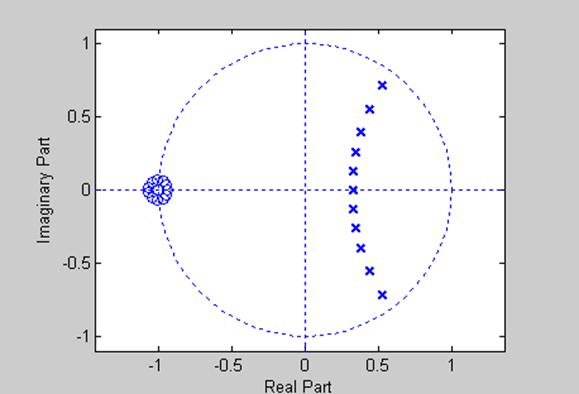
Рис. 25.

Вычисление   оконных функций

Оконные функции  используются для ограничения задания сигнала во временной области  или для ограничения частотного спектра сигнала.  Важными свойствами окон являются их амплитудные спектры. Фазовые характеристики окон имеют линейный характер  и поэтому, как правило, не рассматриваются.

      Примеры некоторых оконных функций. Функция  w=hanning(n)  возвращает  n – точечное  окно Хэннинга  в векторе-столбце w. Коэффициенты окна  Хэннинга вычисляются по выражению

.

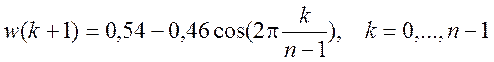Аналогично функция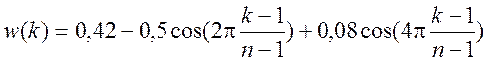 

вычисляет  n – точечное окно Блэкмана.

Среди 14 оконных функция Matlab имеются окна с регулируемыми параметрами.  Примером является окно Кайзера.  Синтаксис соответствующей функции Matlab

Здесь параметр beta определяет минимальное  затухание боковых лепестков  спектра окна.

Функция  w=window(fhandle, n)  возвращает  n – точечное окно типа, задаваемого параметром fhandle.

      Пример  вывода трех окон и их амплитудных спектров с помощью специальной  функции  визуализации окон wvtool(w1,w2,…, wn)

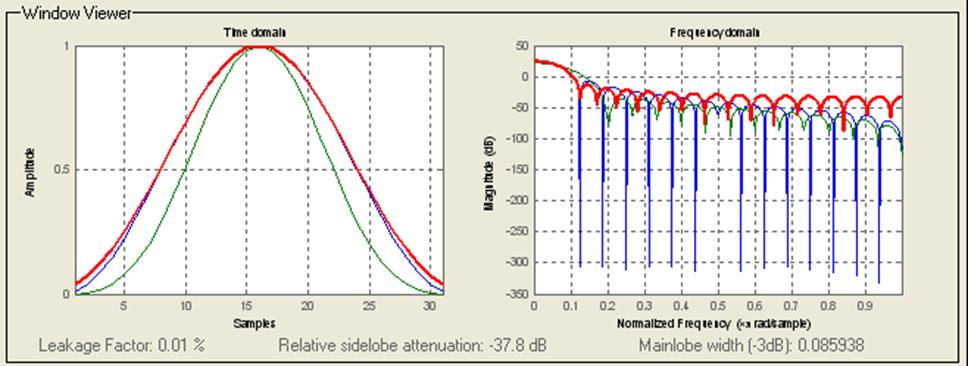
                                                                     Рис. 26.

Оглавление

Введение……………………………………………………………………………………2

Простые вычисления………………………………………………………………………3

Переменные  Matlab………………………………………………………………………..4

Форматы вывода результата……………………………………………………………….5

Вычисления с комплексными числами…………………………………………………...5

Получение справочных сведений в MATLAB…………………………………………...6

Векторы   и   матрицы……………………………………………………………………...7

Операции с матрицами …………………………………………………………………….9

Поэлементные  операции  с массивами…………………………………………………..12

Программирование  в  MATLAB…………………………………………………………13

Построение графиков MATLAB………………………………………………………….17

Полиномы…………………………………………………………………………………..21

Генерирование сигналов…………………………………………………………………..22

Анализ линейных непрерывных систем……………………………………………….....27

Частотные  характеристики и их графики………………………………………………..28

Анализ линейных дискретных систем…………………………………………………....32

Частотные характеристики дискретных систем………………………………………….35

Вычисление оконных функций…………………………………………………………....37