Теория и обработка сигналов MATLAB в ТОС, страница 6

               >> mesh(…)         % строит трехмерные поверхности  со специфицированной

      % окраской

                 Пример.

                  >> [X,Y]=meshgrid([-3:0.1:3]);

                 >> Z=X.^2+Y.^2;

                 >> mesh(X,Y,Z) 

      

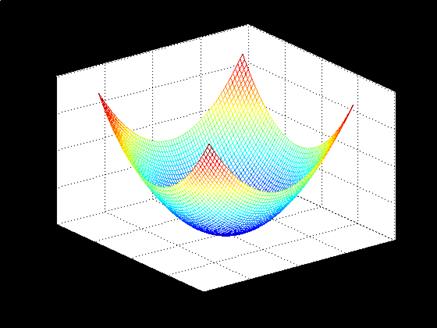
                        Рис.6.

Полиномы

 Matlab представляет полином  как вектор – строку коэффициентов полинома, начиная со старшей степени многочлена.  

Например, полином в Matlab  представляется в виде     >> p = [2   5   -4].

Список наиболее важных команд для работы с полиномами

 roots(p)                определяет  корни полинома в виде вектора – столбца

 polyval(p,x)        вычисляет полином p по значениям вектора x

 conv(p1, p2)        вычисляет произведение полиномов p1 и  p2

 poly2str(p,’s’)     отображает полином как выражение от s

 poly(r)                 вычисляет  полином, заданный вектором корней r.              

Пример. Факторизация полинома    

            >> P=[13  25   3   4];

>> R=roots(P)

R =

  -1.8872         

  -0.0179 + 0.4034i

  -0.0179 - 0.4034i

Генерирование сигналов

Генерирование непериодических сигналов

Функции генерирования часто встречающихся на практике непериодических сигналов:
      1. функция  y = rectpuls(t,w) формирует прямоугольный импульс единичной амплитуды для заданной в векторе t последовательности отсчетов времени, параметр w – ширина импульса

Пример

Fs=10^3;  %  Частота отсчетов

» t=-0.05:1/Fs:0.05;

» A=5;

» tau=0.02;  % Длительность импульсов

» s=-A*rectpuls(t+tau/2,tau)+A*rectpuls(t-tau/2,tau);

» plot(t,s)

» axis([-0.05,0.05,-6,6])

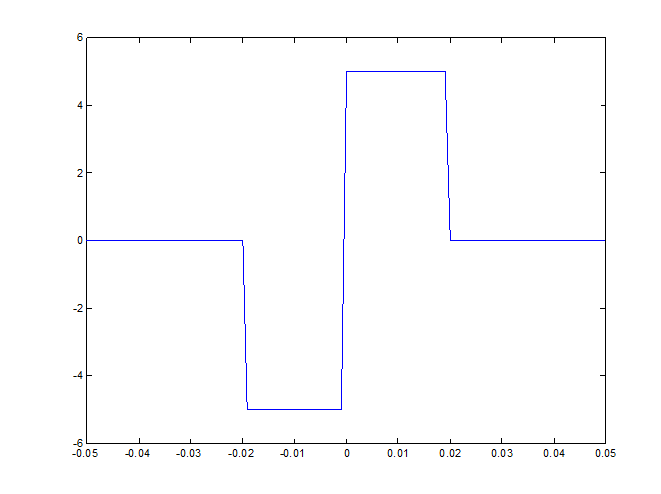
                                                      Рис.7.

2.  функция  y = tripuls(t,w,s) формирует треугольный импульс единичной амплитуды для заданной в векторе t последовательности отсчетов времени, параметры w – ширина импульса,   -1<s<1 – наклон импульса, для симметричного импульса  s = 0.

Пример

» t=0:0.01:10;

» s=0.9*tripuls(t-2,0.8)+1.2*tripuls(t-6,0.5,-1);

» plot(t,s)

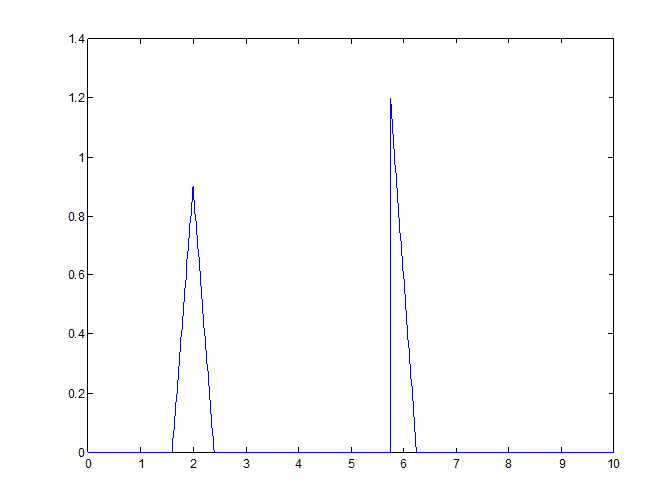
                       Рис.8.

3.  процедура Matlab y = sinc(x) генерирует последовательность значений  функции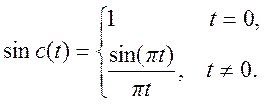

Её следует отличать от функции , в Matlab такая функция определяется по выражению .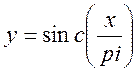

Пример

» t=0:0.01:60;

» y=0.5*sinc(pi*(t-30)/6);

» plot(t,y)

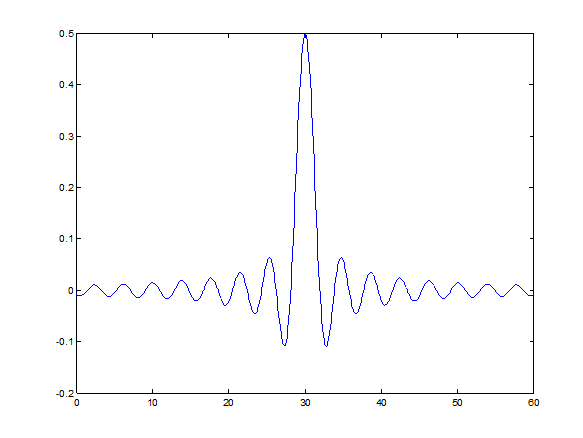
                                                      Рис.9.

4.  Группа функций pulstran() генерирует последовательность импульсов. Её наиболее часто используемый синтаксисy = pulstran(t, d, ‘func’) с помощью параметра ‘func’ позволяет задать форму импульса. Этот параметр может принимать одно из следующих значений:

gauspuls – синусоида, модулированная кривой Гаусса,

rectpuls – импульс прямоуголной формы,

tripuls – треугольный импульс.

Выходной сигнал определяется для значений аргумента, заданных в векторе t, по формуле

y= func(t-d(1))+func(t-d(2))+…

Пример

»  t=0:0.01:10;

» d=0:10/5:10;

» s=pulstran(t,d,'tripuls',1,-1);

» plot(t,s)

 

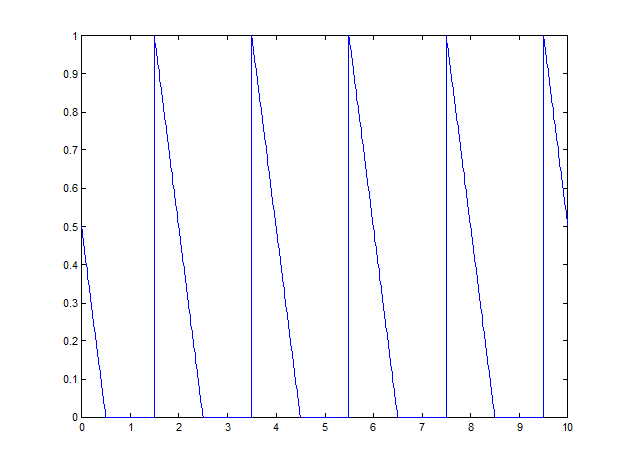
                                                Рис.10.

Генерирование периодических сигналов

Функции Matlab для формирования периодических сигналов различной формы:

1.  Функция y= square(t, duty) генерирует последовательность прямоугольных импульсов с периодом  2π для последовательности отсчетов, определяемой в векторе t, параметр duty задает продолжительность положительной полуволны в процентах от периода
            Пример

» t=0:0.01:50;

» y=0.8*square(pi*t/5,  40);

» plot(t,y)

» axis([0,50,0,1])

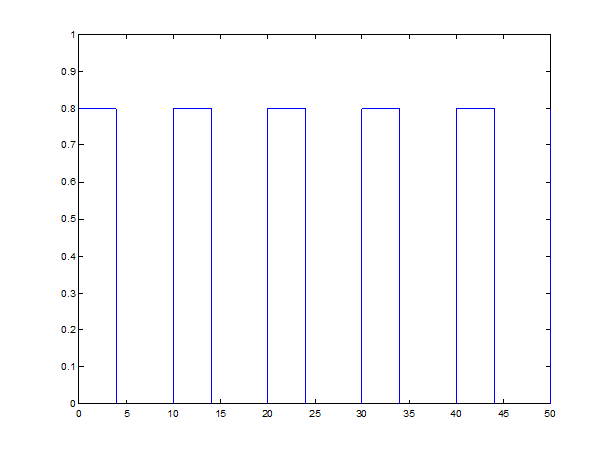
                    Рис.11.

2.  Функция y=sawtooth(t,’width’) предназначена для формирования пилообразного сигнала с амплитудой  и периодом 2π.  Параметр width задается  в интервале от 0 до 1 и определяет часть периода, в котором сигнал возрастает, при этом сигнал на интервале от 0 до 2π*width  увеличивается от -1 до 1, а далее уменьшается от 1 до -1 на интервале от  2π*width  до 2π.

Пример

» t=0:0.01:5*pi;

» y=sawtooth(t,1);

» plot(t,y)

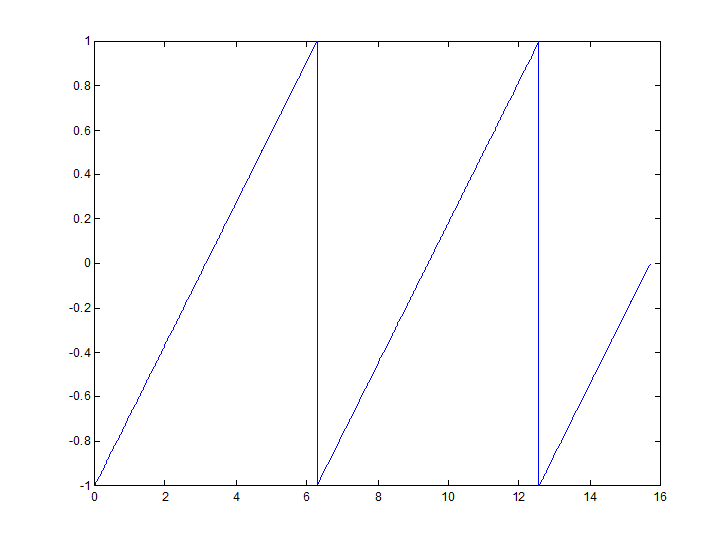
Рис.12.

3.  Функция  y = diric(x, n) формирует последовательность значений функции Дирихле .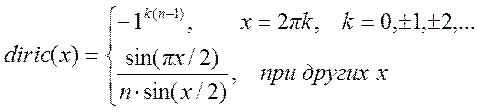

Эта функция является периодической. При нечетных n период равен 2π, при четных период составляет 4π.

Пример

» t=0:0.01:5*pi;

» y=0.8*diric(pi*t/5,6);

» plot(t,y)

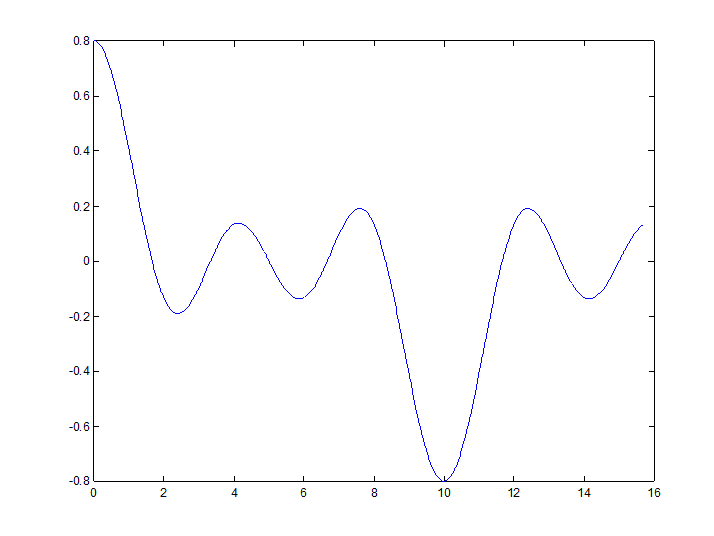
                                                            Рис.13.

Преобразование Лапласа  и  Z – преобразование

 Преобразование Лапласа широко используется для анализа непрерывных динамических систем,  Z - преобразование – для анализа дискретных (цифровых) систем.   

 Наиболее важные команды MATLAB для работы с этими преобразованиями

residue(n,d) – вычисление разложения полинома  n(s) / d(s) на элементарные дроби

step(SYS) -    вычисление/построение графика переходной характеристики непрерывной системы с передаточной функцией  SYS

impulse(SYS) - вычисление/построение графика импульсной характеристики системы SYS

lsym(SYS,u) - вычисление/построение графика выходного сигнала системы SYS при входном векторе u

pzmap(n,d) - вычисление/построение графика нулей и полюсов системы SYS

residuez(n,d) – вычисление разложения полинома  n(z) / d(z) на элементарные дроби в виде функции z^-1

dlsym(n,d,u) - вычисление/построение графика выходного сигнала дискретной системы с системной функцией n(z) / d(z) при входном векторе u

dstep(n,d) -    вычисление/построение графика переходной характеристики дискретной систе-   мы с  передаточной функцией  n(z) / d(z)

dimpulse(n,d) - вычисление/построение графика импульсной характеристики системы n(z)/d(z).

Анализ линейных непрерывных систем

            Передаточная функция непрерывной системы определяется в MATLAB отношением полиномов

,

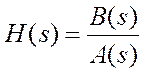где  полином числителя   ,

полином знаменателя      .  Коэффициенты  B(s) и A(s) запоминаются  в векторах  ,  .

            Например,

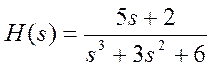
определяется векторами  num = [ 5    2],   den = [1   3   0   6].

            Передаточная функция в полюсно – нулевом представлении

,

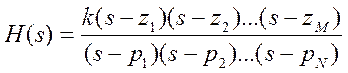где  z_i – нули, p_i – полюса, k –коэффициент усиления системы.

            Для нахождения нулей, полюсов и усиления  по передаточной функции  H(s) используется процедура