Теория и обработка сигналов MATLAB в ТОС, страница 7

,

при этом  z – вектор нулей, p – вектор полюсов, k   - усиление.

            Для перехода от полюсно  - нулевого представления непрерывной системы к передаточной функции служит преобразование

.  

Функция

выполняет разложение на простые дроби передаточной функции, представленной в виде отношения двух полиномов.  Здесь вычеты запоминаются в векторе  r, полюсы – в векторе p, усиление – в k. Формат  [B, A]= residue(z, p, k)  с тремя входными аргументами и двумя выходными выполняет преобразование системы в виде полюсно-нулевого представления в передаточную функцию.

            Построение переходной характеристики (step response) системы может быть осуществлено вводом

                                                            ,

аналогично строится график импульсной характеристики (impulse response) системы

                                                            .

            Для определения отклика (выхода) системы на произвольный входной сигнал используется команда lsim(…). 

Пример. Определим выходной сигнал системы  с передаточной функцией

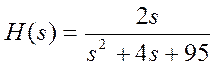
и входным сигналом     .

                        Последовательность команд

            >> n=[2   0];                           % Числитель и знаменатель передаточной функции

>> d=[1   4    95];

>> t= linspace(0,5,301);         % Задание временного интервала

>> u=cos(2*pi*t);                   % Входной сигнал

>> [y,x]=lsim(n, d, u, t);         % Выходной сигнал

>> plot(t,y,'r',t,u,'k');

>> xlabel('Time,  sec'); 

>> ylabel('Amplitude');

Графики входного и выходного сигналов

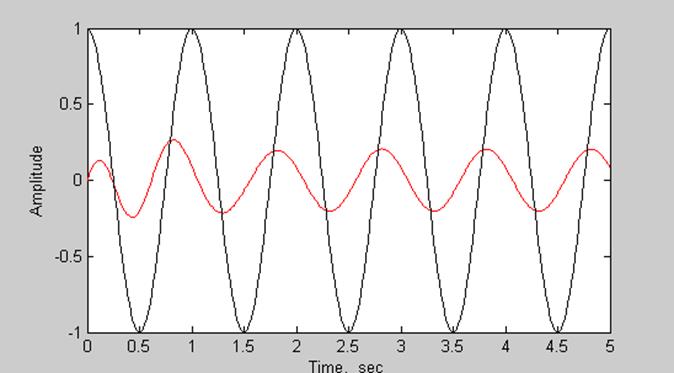
Рис.14.

Частотные  характеристики и их графики

MATLAB-функции  для вычисления и построения графиков частотных характеристик:

 fft(x) – вычисляет дискретное преобразование Фурье вектора x с помощью алгоритмов Быстрого Преобразования Фурье (БПФ)

ifft(x) – вычисляет обратное дискретное преобразование Фурье вектора x с использованием   БПФ

fftshift – производит сдвиг преобразования fft из диапазона (0,  2π) в интервал (-π,  π)

freqs(n,d) – вычисляет частотную характеристику (frequency response) непрерывной системы с передаточной функцией  n(s) / d(s)

freqz(n,d) – вычисляет частотную характеристику (дискретной) системы с передаточной функцией  n(z) / d(z)

bode(n,d) – строит Боде диаграмму непрерывной системы с системной функцией n(s) / d(s).

unwrap(P) – корректирует фазовые углы элементов одномерного массива P при переходе
 через значение π.

Пример построения частотной характеристики  системы с передаточной функцией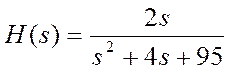 

B=[2  0];

A=[1  4  95];

[H,w]=freqs(B,A);

plot(w/2/pi, abs(H))

set(gca, 'FontName','Times New Roman Cyr','FontSize', 8)

title('Амплитудно - чаcтотная характериcтика')

xlabel('Чаcтота, Гц')

ylabel('Модуль')

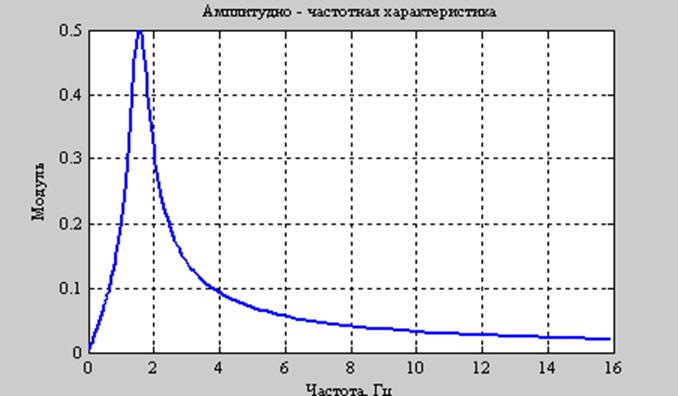
                                                                   Рис.15.

Пример построения  диаграммы Боде и импульсной характеристики

Последовательность команд

» num=[2 0];

» den=[1 4 95];

» % Построение диаграммы полюсов и нулей

» figure(1)

» pzmap(num,den);

» % Диаграмма Боде

» figure(2);

» bode(num,den);

» % Импульсная характеристика

»  figure(3);

» impulse(num,den);

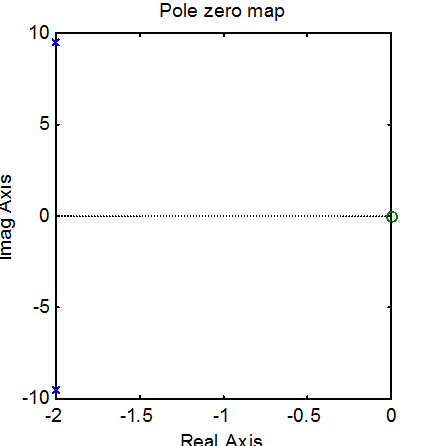
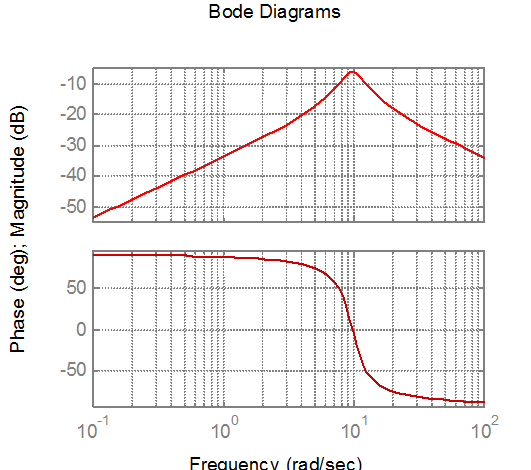
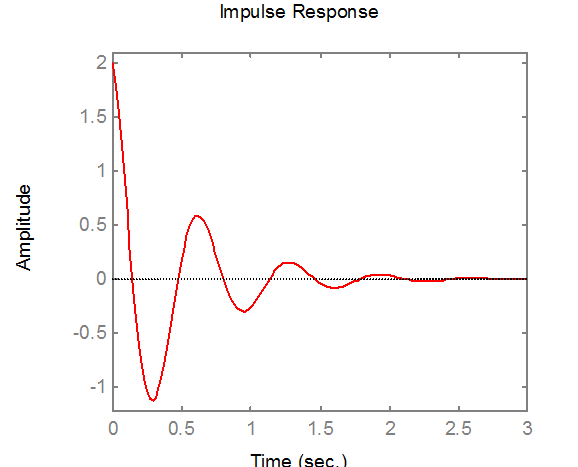
                                              Рис.16.

            Функция fft()  в задачах обработки сигналов применяется, возможно,  чаще всех остальных. Она вычисляет   дискретное преобразование Фурье (ДПФ) вектора x   по выражению

,

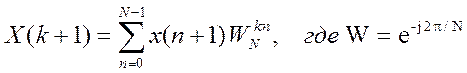при этом - длина вектора x.

Эта же функция с форматом

вычисляет n – точечное дискретное преобразование Фурье.   Если  , то недостающие элементы массива x дополняются нулями (zero pad). Если , то лишние элементы отбрасываются.

Функция   x=ifft(X) вычисляет обратное ДПФ последовательности X. Функция  x=ifft(X,n)  вычисляет n – точечное обратное ДПФ.

Для вычисления функций fft() и ifft() применяются алгоритмы  быстрого преобразования Фурье (БПФ). Этот алгоритм имеет максимальное быстродействие,  когда длина последовательности x равна степени числа 2.  Поэтому желательно использовать последовательности, длина которых равна степени числа 2.

Пример.

% Процедура вычисления и построения спектров 

% сигнала с помощью функции fft()

N=128;  % число точек

Ts=T/(N-1);   % интервал отсчетов  

t=0:Ts:T;  % временной интервал

tau=2;    % длительность импульса

x=rectpuls(t,tau);   % генерирование прямоугольного импульса

figure(1);

subplot(311), plot(t,x), grid    % график сигнала

set(gca,'FontName','Arial Cyr', 'FontSize',8)

title(' График сигнала')

Fmax=1/Ts;   % максимальная частота

df=1/T;    % частотное разрешение

f=-Fmax/2:df:Fmax/2;       

X=fft(x,N);     % БПФ сигнала

Xp=fftshift(X);     % частотный сдвиг

A=abs(Xp);

subplot(312), plot(f,abs(Xp)*Ts), grid

set(gca,'FontName','Arial Cyr', 'FontSize',8)

title(' Амплитудный спектр сигнала')

%S=sinc(f*tau/2)*tau/2;     % преобразование Фурье сигнала

% график

subplot(313), plot(f, angle(Xp)), grid

set(gca,'FontName','Arial Cyr', 'FontSize',8)

xlabel('  Частота,  Гц')

title(' Фазовый спектр сигнала ')

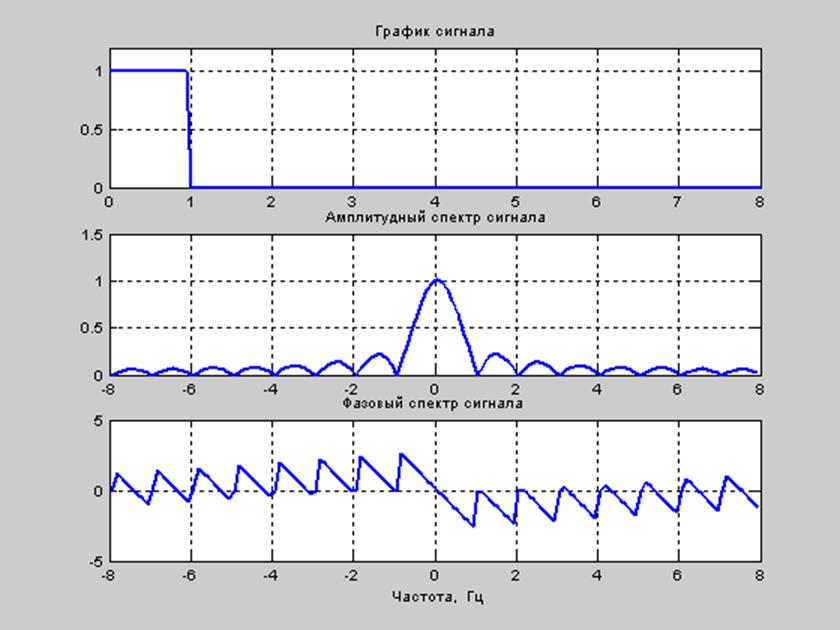
Рис. 17

Анализ линейных дискретных систем

Свертка

Команда

y = conv(x, h) – вычисляет свертку последовательностей x и h. С  помощью свертки вычисляется  сигнал на выходе дискретной системы у с импульсной характеристикой  h и входным сигналом x при нулевых начальных условиях.

[q,   r] = deconv(z,  x) – выполняет операцию, обратную свертке.

Пример

» n=0:10;

» x=ones(1,11);

» h=5*(0.4).^n-5*(0.02).^n;

» y=conv(x,h);

» y=y(1:length(n));

» stem(n,y)

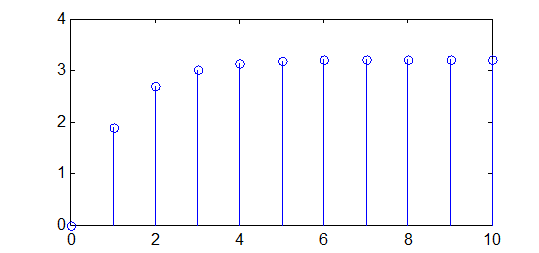
               Рис.18.

Команда  conv может использоваться также для умножения полиномов, conv(a,b) - произведение полиномов, представляемых векторами коэффициентов a  и b.

Передаточная функция дискретной системы

Выражение  вида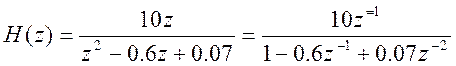

представляется  в MATLAB векторами коэффициентов полиномов числителя и знаменателя

num = [10  0];

den = [1   -0.6   0.07];

Команды dstep и dimpulse вычисляют соответственно переходную и импульсную характеристику системы

Пример.

» n=0:10;

» num=[10   0];   den=[1   -0.6   0.07];