Спектральные представления периодических сигналов: Методические рекомендации по выполнению лабораторной работы

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

Дисциплина  «Теория  и  обработка  сигналов»,     5 - й семестр

ЛАБОРАТОРНАЯ  РАБОТА  № 2

СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ

ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Цель работы:изучение понятия спектра  периодического сигнала, приобретение практических навыков вычисления,  построения  графиков и анализа спектров   сигналов в  среде MATLAB.

Задание и порядок выполнения работы.

1.  Познакомьтесь с разложением в ряд Фурье периодических непрерывных сигналов и понятиями амплитудного и фазового спектров сигнала по учебной литературе, например,  [1] стр. 19 – 27 или  [2] стр. 21 -30.

2.  Ознакомьтесь с демонстрацией  Help | Demos | MATLAB | Graphics | FourierSeriesExpansion. Эта демонстрация Matlab иллюстрирует синтез прямоугольной периодической волны из гармоник сигнала и в наглядной форме показывает идею  разложения сигнала в ряд Фурье.

3.  Получите аналитически коэффициенты разложения в ряд Фурье  (комплексный или тригонометрический)  для сигнала, заданного в индивидуальном задании (Приложение 1), запишите после этого ряд Фурье сигнала. Для проверки полученного результата преобразуйте его к виду ряда Фурье, приведенного в ответе к заданию. Постройте приближенные графики (эскизы)  амплитудного и фазового спектров  сигнала в среде MS WORD.  При выполнении задания п.2 можно ориентироваться на пример, приведенный в Приложении 2.

4.  Напишите  и выполните файл-сценарий (М-файл), позволяющий построить в Matlab  графики амплитудного и фазового спектров сигнала на основе вычислений в п.2. Соответствующий пример представлен в Приложении 3.

5.  Определите спектр Фурье сигнала с помощью функции fft() Matlab. Эта функция является основной процедурой проведения спектрального анализа в Matlab. Ознакомьтесь по справочной системе с данной функцией.
Процедура fft() вычисляет дискретное преобразование  Фурье сигналов по выражению 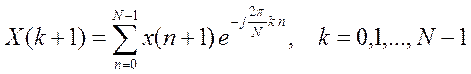 .  От  коэффициентов Фурье дискретного периодического сигнала x[n] с периодом N 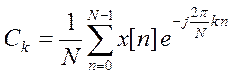     значения X(k+1) отличаются множителем  и смещением индексов на 1, так как индексация массивов в Matlab начинается с 1.
Поэтому коэффициенты ряда Фурье периодического дискретного по времени  сигнала равны  fft()/N, где N – размер (длина) вектора fft().
        Определите коэффициенты ряда Фурье  с помощью fft() для сигнала, заданного в п.2,  постройте и сопоставьте графики амплитудного спектра по п.3 и п.4. В Приложении 4 приведен пример соответствующей программы.  Поясните характер и особенности получившихся спектров.  Обратите внимание на периодический характер спектра, вычисленного с помощью fft(), объясните причину периодичности.    

6.  Составьте и выполните файл-сценарий для исследования сходимости ряда Фурье к исходному периодическому сигналу (индивидуальное задание, п.2) в соответствии с примером,  приведенным в Приложении 5.
Постройте при этом также график исходного периодического сигнала.

Пронаблюдайте сходимость  ряда  для четырех значений числа членов ряда и явление Гиббса, возникающее при конечном числе членов ряда Фурье у сигналов с разрывами поведения функций. Объясните характер и особенности сходимости ряда Фурье к сигналу.
Пояснение. Для увеличения фрагмента графика используйте команду zoomon – включение режима увеличения, zoomoff – отключение увеличения.

7.  Факультативное  задание.  Выполните задачу синтеза периодического сигнала, заданного в индивидуальном задании (п.2), с использованием пакета Simulink.
             Simulink – это пакет расширения Matlab, предназначенный для моделирования динамических систем. Ввод элементов исследуемых систем в Simulink производится в диалоговом режиме с помощью технологии Drag-and-Drop. В результате формируется так называемая S-модель исследуемой системы. Модель можно сохранить в файле типа  .mdl.
            Для построения модели Фурье-синтеза сигнала создайте новый файл с помощью команды меню File/New/Model и расположите необходимые блоки в окне модели. Вид модели представлен в Приложении 6. Для создания подобной модели используйте окно SimulincLibraryBrowser. Из раздела Sources (Источники) библиотеки перенесите в окно модели блок Constant и 5-7 блоков SinWave, из раздела MathOperations  – блок Sum, из раздела SignalRouting – блок мультиплексора (Mux), из раздела Sinks(Приемники)- два блока Scope (Индикатор).
          С помощью двойного щелчка мыши или контекстного меню на блоке Sum откройте окно BlockParameters (Блок параметров)  и установите необходимое число входов сумматора.  В блоке параметров каждого  SinWave установите нужные для синтеза сигнала значения амплитуды и угловой  частоты (рад/с) каждой гармоники, при необходимости – фазу гармоники.
          Соедините блоки между собой с помощью мыши. После создания, настройки и сохранения модели запустите её на исполнение с помощью команды меню Simulation/Start или кнопки Start.  С помощью контекстного меню (правая кнопка мыши) на блоке Scope откройте окно Scope и пронаблюдайте результат решения задачи Фурье-синтеза сигнала. В дальнейшем поместите копии модели и окна Scope в отчет по работе.
Сделайте вывод по синтезу периодического сигнала с помощью гармоник.

8.  Составьте отчет по лабораторной работе. В отчете должны быть представлены

§  титульный лист,

§   название и цель работы,