Информатика и выч. техника \ Теория и обработка сигналов

Спектральные представления периодических сигналов: Методические рекомендации по выполнению лабораторной работы, страница 2

§  формулировки пунктов работы, команды и  .m – файлы,
графики, комментарии, выводы по работе.

9.  Проверьте свою подготовку по контрольным вопросам, отчитайтесь в   выполнении работы.

Литература

1.  Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ,  1998 - ч.1.

2.  Сергиенко А.Б. Цифровая обработка сигналов / СПб.: Питер, 2003.

3.  Щетинин Ю.И. Теория и обработка сигналов. Методические указания к решению задач и упражнений по курсу.- Новосибирск: Изд-во НГТУ, 2007.

4.  Лазарев Ю.Ф.  MatLAB 5.x. – К.: Издат. группа BHV, 2000.

5.  Потемкин В.Г., Рудаков П.И.. MATLAB 5 для студентов. -  2-е изд., испр. и дополн. – М.: ДИАЛОГ-МИФИ, 1999.

Web – ресурсы

1.  http://tiger.cs.nstu.ru/tos/periodic/start.html

2.  http://www.jhu.edu/~signals/fourier2/index.html

3.  http://users.ece.gatech.edu/~bonnie/book/OnlineDemos/ConvergenceOfFourierSeries/index.htm

Контрольные вопросы и упражнения.

1.  Запишите ряд Фурье в тригонометрической и комплексной формах, объясните их связь.

2.  Объясните физический смысл разложения сигнала в ряд Фурье.

3.  Запишите и объясните разложение в ряд Фурье  периодической последовательности прямоугольных импульсов. Каково поведение амплитудного спектра такого сигнала при   Т→ ∞?

4.  Какие сигналы (функции) могут быть разложены в ряд Фурье?

5.  Сформулируйте особенности скорости сходимости ряда Фурье для непрерывных функций и функций с разрывами.

6.  Какой характер имеет разложение в ряд Фурье для четных функций?

7.  Разложите в ряд Фурье периодический с периодом 2T сигнал, который на отрезке [-T, T] задается выражением x(t)=|t|. Постройте амплитудный спектр сигнала  для T=5.

8.  Какие особенности имеет разложение в ряд Фурье для нечетных Функций?

9.  Запишите ряд Фурье периодического с периодом T =2 сигнала, заданного на интервале [-1, 1]  выражением  .

10. Что такое эффект Гиббса? Каковы причины его возникновения?

11. Сформулируйте определение и физический смысл амплитудного спектра периодического сигнала.

12. Каков характер амплитудного спектра периодического сигнала? Как изменяются амплитуды гармоник с изменением номера для непрерывного на периоде сигнала и для сигнала с разрывами?

13. Поясните смысл фазы гармоники. Что такое фазовый спектр периодического сигнала?

14. Запишите и объясните физический смысл теоремы Парсеваля для периодических сигналов.

15. Как определить коэффициенты ряда Фурье с помощью процедуры fft()?

16. В среде Matlab с помощью функции fft() определите амплитудный спектр изображенного ниже периодического сигнала и постройте его график

 






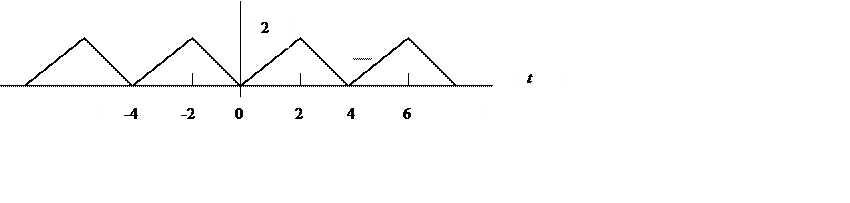Приложение 1.       Варианты индивидуальных заданий.

1. 

Коэффициенты ряда Фурье

,                 

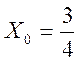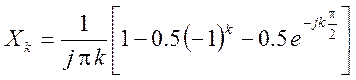
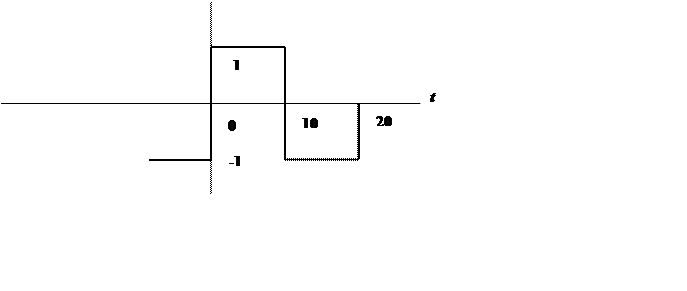2.

Ряд  Фурье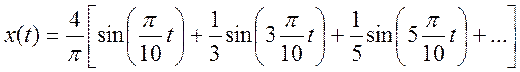       

3.

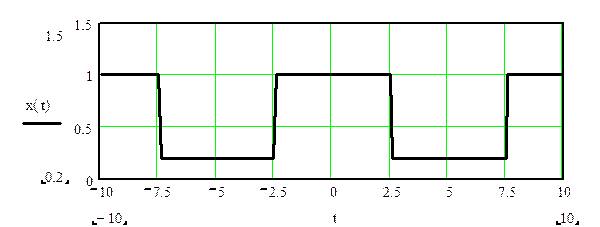
Ряд  Фурье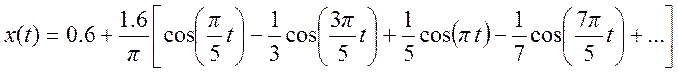  

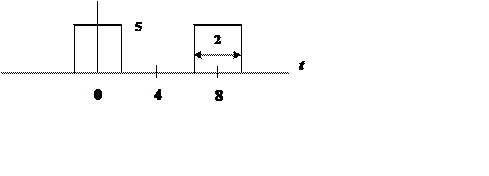4.

Ряд  Фурье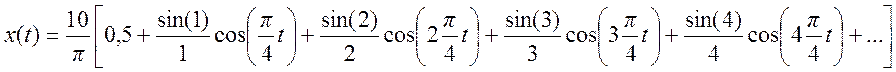  

5. 

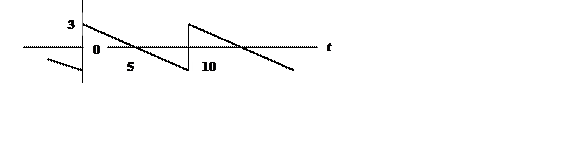
Ряд  Фурье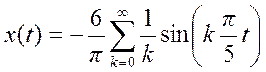     

6.

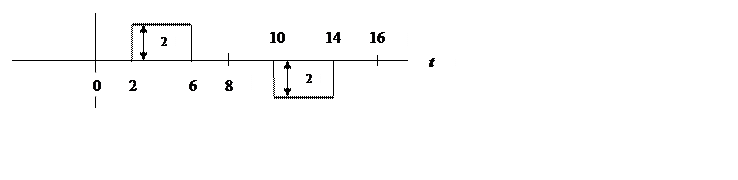
Ряд Фурье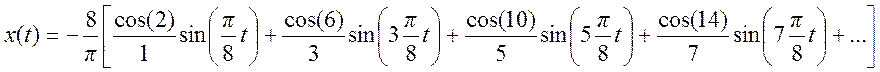

7. 

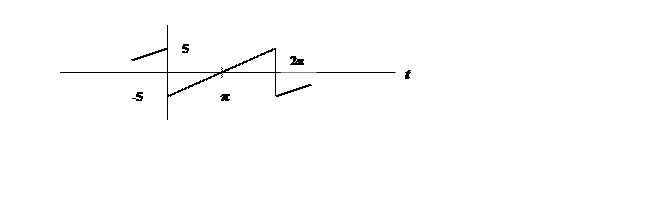
Ряд  Фурье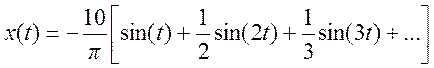   

8.

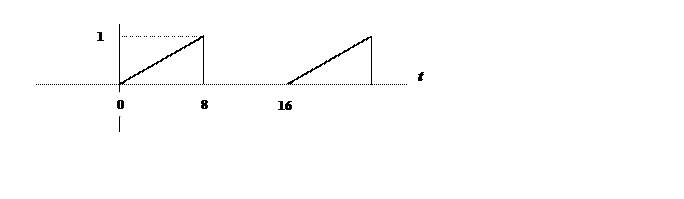
Ряд Фурье

 

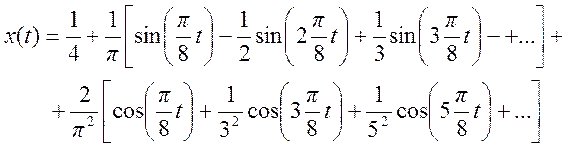
9.

Ряд Фурье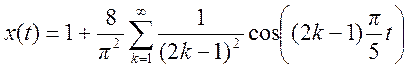                 

10.

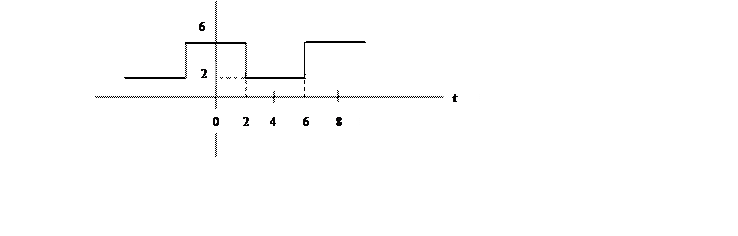
Ряд Фурье

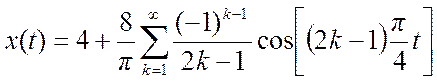
Приложение 2.  Пример разложения сигнала в ряд Фурье.

Вид сигнала

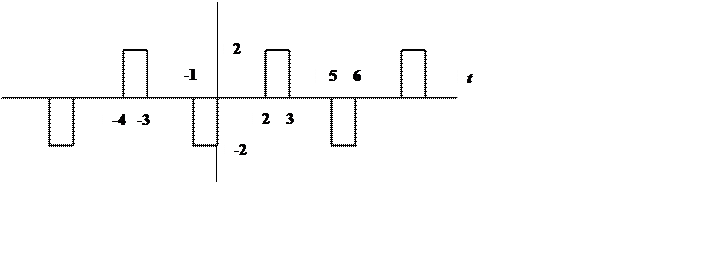
Частота основной гармоники  .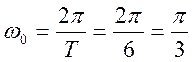 

Коэффициенты комплексного  ряда  Фурье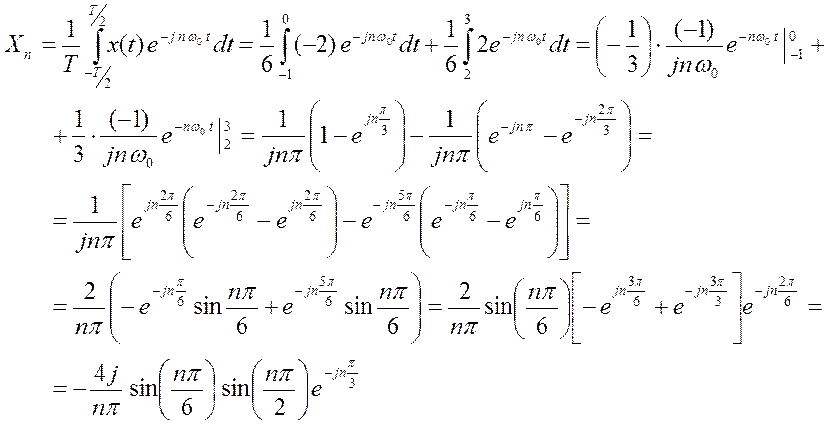

Для  n = 0   .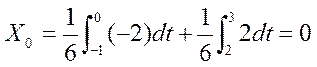

В частности,    ,      ,  ,

,  , , ,.

Ряд Фурье   .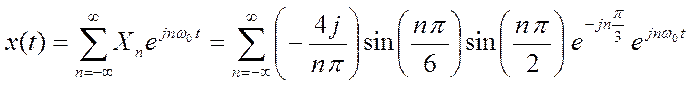

График амплитудного спектра сигнала

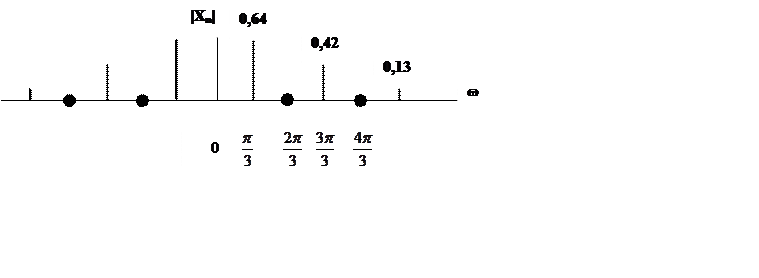
Приложение 3.    М-файл для построения графиков амплитудного и фазового спектров сигнала.

% Файл - сценарий для построения графиков спектров

    w0 = pi/3;

 n1=1:15;

 cn=-4*j./n1/pi.*sin(pi*n1/6).*sin(n1*pi/2).*exp(-j*n1*pi/3);

 n2=-15:-1;1

 c_n=-4*j./n2/pi.*sin(pi*n2/6).*sin(n2*pi/2).*exp(-j*n2*pi/3);

 Cn=[c_n 0 cn];

 n3=[n2 0 n1];

 n=-15:15;

 figure(1), subplot(121),stem(n*w0,abs(Cn))

 xlabel('Frequency,  rad/sec')

 title('|Cn|')

 subplot(122),stem(n*w0,angle(Cn))

 xlabel('Frequency,  rad/sec')

 title('angle(Cn) in rad')

Графики амплитудного и фазового спектров сигнала

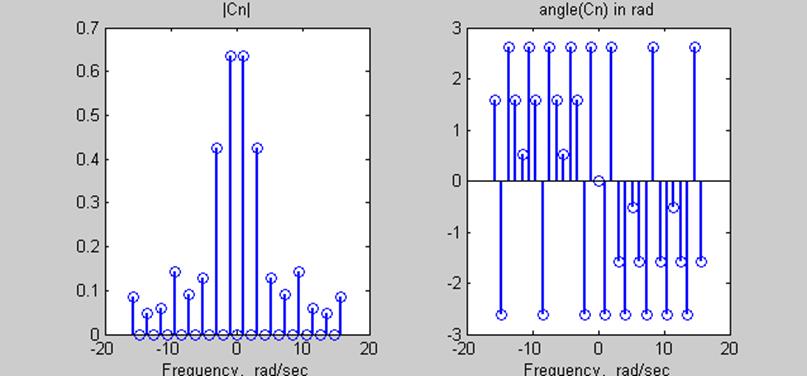
Приложение 4.  М-файл для вычисления коэффициентов ряда Фурье  сигнала с помощью процедуры fft().

T=6;% период сигнала

t=0:T/63:T;% временной интервал

x=2*rectpuls(t-2.5,1)-2*rectpuls(t-5.5,1);% генерирование сигнала

figure(1);

subplot(311), plot(t,x) % график сигнала

title(' График сигнала')

k=0:63;

% коэффициенты ряда Фурье

C=-4*j./k/pi.*sin(pi*k/6).*sin(k*pi/2).*exp(-j*k*pi/3);

% график амплитудного спектра

subplot(312),

stem(2*pi*k/T, abs(C));

title(' Амплитудный спектр сигнала')

y=fft(x,64);% Дискретное преобразование Фурье сигнала

% график ДПФ

subplot(313), stem(2*pi*k/T, abs(y)/64)

xlabel(' Угловая частота,  рад/сек')

title(' Амплитудный спектр сигнала по процедуре fft')

Приложение 5.  Файл-сценарий приближения сигнала рядом Фурье.

T=6;

w0 = 2*pi/T;

t = 0:T/1000:T*4/3; % интервал времени

% исходный сигнал

x1=2*rectpuls(t-2.5,1)-2*rectpuls(t-5.5,1);

N = input('Number of harmonics    ');

c0 = 0;

x = c0*ones(1,length(t)); % постоянная   составляющая

for n=1:N,

% коэффициенты Фурье

cn = -4*j/n/pi*sin(pi*n/6)*sin(n*pi/2)*exp(-j*n*pi/3);

c_n = conj(cn);

% Приближение сигнала рядом Фурье

x = x + cn*exp(j*n*w0*t) + c_n*exp(-j*n*w0*t);

end

plot(t,x,t,x1, '--r'), grid

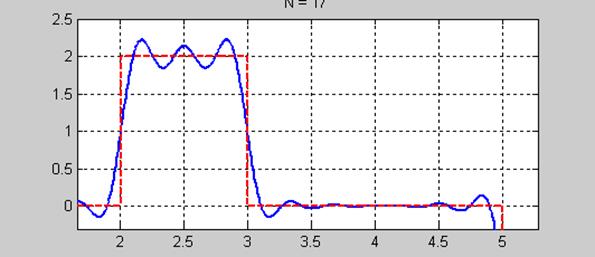
title(['N = ',num2str(N)])

Графики, число членов ряда N=17

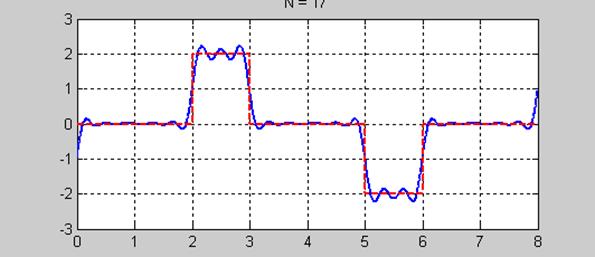
Явление Гиббса (увеличенный масштаб)

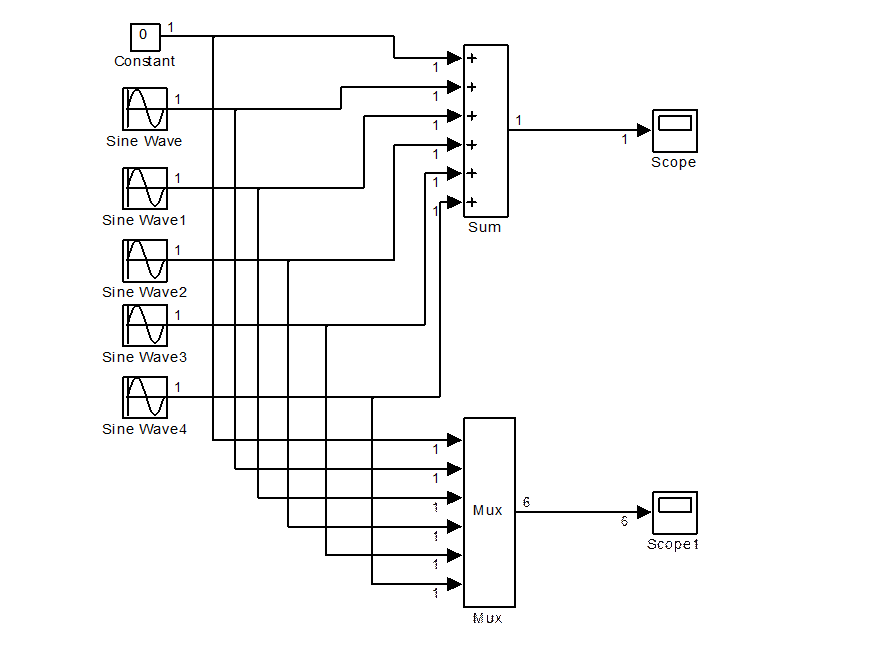
Приложение 6.   Вид S - модели Фурье-синтеза сигнала

Составил  доц.  Щетинин  Ю.И.

Скачать файл